Tenségrité — Wikipédia
La tenségrité, intégrité en tension ou compression flottante est un principe structurel basé sur un système de composants isolés en compression à l'intérieur d'un réseau en tension continue, et disposés de telle manière que les éléments comprimés (généralement des barres ou des entretoises) ne se touchent pas tandis que les éléments précontraints (en) en tension (généralement des câbles ou des tendons) délimitent spatialement le système[1].
Le terme tensegrity a été inventé par R. Buckminster Fuller dans les années 1960 comme un mot-valise pour tensional integrity (« intégrité en tension »)[2]. Le terme floating compression (« compression flottante »), a principalement été utilisé par l'artiste constructiviste Kenneth Snelson (en).
La tenségrité est un concept inventé et utilisé en architecture, étendu à d'autres systèmes mécaniques (utilitaires[3] ou artistiques[4]), utilisé aussi en biologie, et un sujet d'étude en mathématiques[a].
Architecture
[modifier | modifier le code]
La structure de tenségrité est un système réticulé spatial constitué de barres dont la rigidité et la stabilité sont dues à son état d'autocontrainte. L'état de tenségrité est un « état d'autoéquilibre stable du système, dont les composants comprimés constituent un ensemble discontinu à l'intérieur d'un ensemble continu de composants tendus »[6]. La structure se stabilise par le jeu des forces de tension et de compression qui s'y répartissent et s'y équilibrent. Les structures établies par la tenségrité sont donc stabilisées, non par la résistance de chacun de leurs constituants mais par la répartition et l'équilibre des contraintes mécaniques dans la totalité de la structure. Ainsi, un système mécanique comportant un ensemble discontinu de composants comprimés au sein d'un continuum de composants tendus peut se trouver dans un état d'équilibre stable. Ce qui signifie, par exemple, qu'en reliant des barres par des câbles, sans relier directement les barres entre elles, on arrive à constituer un système rigide.
Les dômes géodésiques sont des structures réticulées ; ce ne sont pas des systèmes répondant au concept de tenségrité[réf. souhaitée]. On peut citer à cet égard les dômes géodésiques de la Biosphère de Montréal (Fuller, 1967) ou de La Géode à Paris (Fainsilber, 1985). La confusion vient du fait que Buckminster Fuller souhaitait réaliser un dôme en utilisant le concept de tenségrité mais les technologies de l'époque et les moyens de calcul ne lui ont pas permis de le faire.
Les recherches sur la tenségrité se tournent aussi vers les sciences naturelles, comme la biologie. Ainsi, les cytosquelettes des cellules animales seraient de telles structures : les microtubules sont au centre d'un réseau de contraintes compressives exercées par des filaments (cf. Tenségrité (biologie)).
Une origine contestée
[modifier | modifier le code]

Il semble bien que l'idée d'une structure tridimensionnelle dont l'équilibre se fait au moyen de forces de compression et de tension soit antérieure à 1949. Ainsi, une œuvre de l'artiste soviétique Karl Ioganson (de) (1890-1929), nommée Construction systématique et datée de 1921, repose sur le même principe[7], avec néanmoins l'absence d'autocontrainte, un des principes de la tenségrité.
Les huit modèles de Karl Ioganson
[modifier | modifier le code]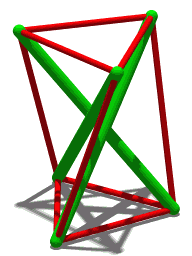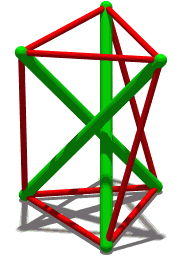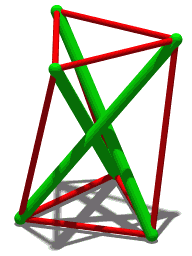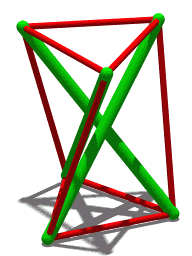

Avec l'œuvre précédente, le peintre et sculpteur Karl Ioganson présente, en trois versions, à l'exposition de l'Obmokhou à Moscou une croix faite de trois tasseaux, non vissés entre eux et reliés par des tenseurs qui ainsi tiennent en équilibre stable. Il présente quatre carrés entrelacés maintenus en équilibre par des tenseurs dans deux versions. Enfin, il présente un prisme auto-tendu, sous le titre « Construction de tiges et de tenseurs »[8].
Les brevets de 1949
[modifier | modifier le code]Cependant, les brevets américains ont été obtenus par Richard Buckminster Fuller, qui aurait donné son nom à la tenségrité (tensegrity = tensile integrity, ce qui signifie que le réseau tendu est continu). Richard Buckminster Fuller aurait recréé le concept du dôme géodésique lors de l'été 1949 au Black Mountain College, avec l'appui de certains élèves et professeurs, dont Kenneth Snelson (en), un artiste qui sera un des premiers à utiliser la tenségrité dans l'architecture. Celui-ci affirmera que Richard Buckminster Fuller lui a volé sa découverte.
En même temps, David Georges Emmerich (1925-1996) popularise ce système en France sous le nom de « systèmes autotendants » dans sa demande de brevet déposée en 1963. Le terme, bien que mieux approprié[réf. nécessaire], ne sera pas conservé.
« Cette curieuse structure, assemblée de trois barres et de sept tirants, était manipulable à l'aide d'un huitième tirant détendu, l'ensemble étant déformable. Cette configuration labile est très proche de la protoforme autotendante à trois barres et neuf tirants de notre invention. »
— David Georges Emmerich[9].
Dans les années 1980, le chercheur montpelliérain René Motro et son équipe au Laboratoire de mécanique et génie civil (LMGC), laboratoire mixte de l'université de Montpellier et du CNRS, ont mené des recherches sur la tenségrité et ont prouvé que l'on pouvait construire grâce à ce principe. Depuis, le LMGC est un centre de recherche important sur la tenségrité et de nombreuses thèses y sont publiées.[réf. nécessaire]
Exemples
[modifier | modifier le code]- Le Kurilpa Bridge à Brisbane, en Australie,
- la Tour du Millénaire à Gedinne en Belgique.
- la Needle Tower de Kenneth Snelson exposée au Hirshhorn Museum and Sculpture Garden.
Biologie
[modifier | modifier le code]En biologie, le concept de tenségrité est utilisé comme modélisation en biomécanique pour expliquer la solidité des structures. Le principe a été emprunté à la tenségrité en architecture en particulier par Donald Ingber (en), de l'université Harvard.
Cellules et matrice extracellulaire
[modifier | modifier le code]En biologie cellulaire, les structures de tenségrité sont des systèmes réticulés constitués, dans l'espace, d’éléments quasi rigides isolés et comprimés par un réseau continu d’éléments élastiques en tension. Le système est donc auto-contraint : c'est l'ensemble des forces élastiques qui s'exercent sur le squelette des cellules qui maintient solidement la forme de chaque cellule puis de l'ensemble.
Le cytosquelette (squelette des cellules) comporte différents constituants : les microtubules (qui résistent mieux en compression), les microfilaments ou filaments d'actine (qui résistent mieux en tension) et les filaments intermédiaires (qui jouent un rôle dans la stabilité de la structure d'une cellule). Le cytosquelette peut être considéré comme une structure en tenségrité. Même s'il existe d'autres hypothèses, les observations attestent que la tenségrité dans les cellules est crédible[10].
De même, la matrice extracellulaire et les complexes d'adhésion focale[Quoi ?] pourraient également être des structures en tenségrité.
Vertébrés
[modifier | modifier le code]Chez les Vertébrés, le système musculo-squelettique (os, muscles, fascias) peut également être perçu comme un système de tenségrité, les os étant comprimés par la tension apportée par les muscles (via les tendons) et les ligaments eux-mêmes tendus.
La tenségrité est à l'origine de la stabilité de la station debout des oiseaux, qui peuvent dormir perchés sur un fil électrique. Elle est notamment assurée par la présence d'un tendon qui passe à l'arrière du genou à travers une boucle ligamentaire de sorte à le maintenir dans son axe, une particularité anatomique unique[11],[12].
Notes et références
[modifier | modifier le code]Notes
[modifier | modifier le code]Références
[modifier | modifier le code]- Gómez-Jáuregui 2010, p. 19.
- (en) Randel L. Swanson, « Biotensegrity: A Unifying Theory of Biological Architecture With Applications to Osteopathic Practice, Education, and Research — A Review and Analysis », The Journal of the American Osteopathic Association (en), vol. 113, no 1, , p. 34–52 (DOI 10.7556/jaoa.2013.113.1.34
 ).
). - Oliveira et Skelton (2009).
- (en) Kenneth Snelson, « The Art of Tensegrity », International Journal of Space Structures, vol. 27, nos 2-3, (DOI 10.1260/0266-3511.27.2-3.71).
- Ma (2023).
- Pugh (1976).
- Voir photo p. 71 de L'avant garde russe, Andréi Nakov, Éd. Fernand Hazan, 1984, (BNF 43443347).
- in Kahn Magomedov, "chap, les constructions spatiales de Karl Ioganson", L'Inkhouk, Naissance du constructivisme, Infolio, Collection Archigraphy, Poche, Paris, 2013, publié à Moscou en 1994, p. 232-238 (ISBN 978-2-88474-715-8)
- David Georges Emmerich, Structures Tendues et Autotendantes, In monographie de géométrie constructive, Éd. École d'Architecture Paris-La-Villette, 1988, p. 30-31.
- (en) Stamenovic D, Ingber DE, Department of Biomedical Engineering, Boston University, USA & Harvard Institute for Biologically Inspired Engineering, Cambridge, USA, « Tensegrity-guided self assembly: from molecules to living cells », Soft Matter 5, , p. 1137–1145 (lire en ligne
 )
) - Mehdi Harmi, « Pourquoi les oiseaux ne tombent pas en dormant », sur Journal du CNRS, (consulté le ).
- (en) Anick Abourachid, Christine Chevallereau, Idriss Pelletan et Philippe Wenger, « An upright life, the postural stability of birds: a tensegrity system », Journal of the Royal Society Interface (en), vol. 20, no 208, (DOI 10.1098/rsif.2023.0433).
Voir aussi
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]- (en) Anthony Pugh, An introduction to tensegrity, Berkeley et Los Angeles, University of California Press, , 109 p. (ISBN 0-520-02996-8 et 0-520-03055-9)
- (en) René Motro, Tensegrity: Structural Systems for the Future, Hermes Science Publishing, , 237 p. (ISBN 1-9039-9637-6, présentation en ligne)
- (en) Mauricio C. Oliveira et Robert E. Skelton, Tensegrity Systems, New York, Springer, , 230 p. (ISBN 978-0-387-74241-0 et 978-1-4419-4491-7, DOI 10.1007/978-0-387-74242-7)
Architecture
[modifier | modifier le code]- David Georges Emmerich, brevet n°1.377.290, Construction de réseaux autotendants demandé le , délivré le (lire en ligne)
- (en) Keneth D. Snelson, patent 3,169,611 Continuous tension, discontinuous compression structures, présenté le , délivré le (lire en ligne)
- (en) Richard Buckminster Fuller, Synergetics : Explorations in the Geometry of Thinking, London, Collier Macmillan Publishers,
- (en) A. Pugh, An Introduction To Tensegrity, Éd. University of California Press, Berkeley, USA, 1976
- David Georges Emmerich, Structures tendues et autotendantes. Monographies de géométrie constructive, Éditions de l'École d'architecture de Paris La Vilette, , 420 p.
- Groupe Recherche et Réalisation de Structures Légères, sous la direction de René Motro, rapport de recherche Système de tenségrité à double nappe et double courbure, Ministère de l'Équipement et du Logement, École d'Architecture Languedoc-Roussillon, Montpellier, juin 1989 (lire en ligne)
- René Motro, « Systèmes de tenségrité: structures autocontraintes constituées de barres et de câbles », Revue construction métallique, no 2, , p. 3-16
- (en) Robert E. Skelton, J. William Helton, Rajesh Adhikari, Jean-Paul Pinaud et Waileung Chan, chap. 17 « An Introduction to the Mechanics of Tensegrity Structures », dans The Mechanical Systems Design Handbook, CRC Press, , 872 p. (DOI 10.1201/9781420036749, présentation en ligne)
- E. Fest et I. F. C. Smith, « Deux structures actives de type tensegrité », Revue Construction métallique, no 3, , p. 19-27
- René Motro et Stefan-J. Medwadowski, Tenségrité, Hermes Science Publications, 2005
- (en) Valentín Gómez-Jáuregui, Tensegrity Structures and their Application to Architecture, Santander, Servicio de Publicaciones de la Universidad de Cantabria, (ISBN 978-84-8102-575-0)
- Jean-Michel Courty et Édouard Kierlik, « La tenségrité et la table impossible », Pour la science, no 522, , p. 88-90
Biologie
[modifier | modifier le code]- Sylvie Wendling, Christian Oddou et Daniel Isabey, « Approche structurale de la mécanique du cytosquelette : solide alvéolaire vs modèle de tenségrité », Comptes Rendus de l'Académie des Sciences, iIB - Mechanics-Physics-Astronomy, vol. 328, no 1, , p. 97-104 (DOI 10.1016/S1287-4620(00)88423-9)
- (en) Donald E. Ingber, « Tensegrity I. How Structural Networks Influence Cellular Information Processing Networks », Journal of Cell Science (en), vol. 116, no 7, , p. 1157-1173 (DOI 10.1242/jcs.00359
 )
) - (en) Donald E. Ingber, « Tensegrity II. Cell structure and hierarchical systems biology », Journal of Cell Science (en), vol. 116, no 8, , p. 1397-1408 (DOI 10.1242/jcs.00360
 )
) - Bernard Maurin, Patrick Cañadas et René Motro, « Modélisation en mécanique cellulaire par systèmes de tenségrité », Techniques de l'ingénieur, (HAL hal-00397676)
Mathématiques
[modifier | modifier le code]- (en) Jing Yao Zhang et Makoto Ohsaki, Tensegrity Structures : Form, Stability, and Symmetry, Springer, , 313 p. (ISBN 978-4-431-54812-6 et 978-4-431-56356-3, DOI 10.1007/978-4-431-54813-3)
- (en) Shuo Ma, Muhao Chen, Hongying Zhang et Robert E. Skelton, « Statics of integrated origami and tensegrity systems », International Journal of Solids and Structures, vol. 279, , article no 112361 (DOI 10.1016/j.ijsolstr.2023.112361)
Liens externes
[modifier | modifier le code]
Architecture
[modifier | modifier le code]- Site officiel de Kenneth Snelson.
- Tenségrité du Marcelo Pars.
- Équipe Conception en Structures du LMGC.


 French
French Deutsch
Deutsch