有限オートマトン

有限オートマトン(ゆうげんオートマトン、英: finite automaton)または有限状態機械(
有限オートマトンは様々な問題に応用でき、半導体設計の自動化、通信プロトコル設計、構文解析などの工学面での応用がある。生物学や人工知能研究では状態機械(群)を使って神経系をモデル化し、言語学では自然言語の文法をモデル化したりする。
概念と用語
[編集]状態[注 1]は、システムの振る舞いのノードであり、システム内で遷移[注 2]を実行するトリガーを待っている。一般に状態は、同じトリガーに対してシステムの反応が常に同じではない場合に導入される。例えば、カーラジオのシステムでは、特定のラジオ局の放送を聴いている状態で「次へ」というトリガーは次のラジオ局(の放送受信)への移行を意味する。しかし、CDプレーヤーのシステムでは、「次へ」は次のトラックへの移行を意味する。これらは、同じトリガーであっても現在状態によって異なる動作を引き起こす。一部の有限オートマトンの表現では、次のように動作[注 3]と状態を対応付けることもある。
遷移[注 6]は、条件が満たされたときまたはイベントを受信したときに実行される動作の集合である。
表現
[編集]

状態遷移図
[編集]有限オートマトンについてその振る舞いを直接的に、状態をノード(節)とし遷移をエッジ(辺あるいは矢印)とした、ネットワーク構造(グラフ理論・グラフ (データ構造) )の図にしたものが状態遷移図である。
状態遷移表
[編集]有限オートマトンについて、その遷移規則(関数)を表にしたものが状態遷移表である。現在の状態(例えばB)と入力(例えばY)の交差するところに次の状態(例えばC)を示す。以下にごく単純な一例を示す。
| 現在状態 → 入力 ↓ | 状態A | 状態B | 状態C |
|---|---|---|---|
| 入力X | ... | ... | ... |
| 入力Y | ... | 状態C | ... |
| 入力Z | ... | ... | ... |
UMLステートマシン
[編集]統一モデリング言語(UML)には状態機械(ステートマシン)を記述するための豊富な意味論と記法がある。UMLの状態遷移図は従来の有限オートマトンの主な利点を踏襲しつつ、その欠点を克服している。大きな拡張としては、状態の階層化や直交状態の導入があり、動作の記法も拡張されている。ミーリ・マシンもムーア・マシンも記述できる。ミーリ・マシンのように状態だけでなく、イベント(入力)をきっかけとして遷移するようにも書けるし、ムーア・マシンのように遷移ではなく状態と開始動作や終了動作を対応付けることもできる。
SDLステートマシン
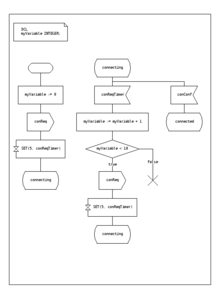
[編集]仕様及び記述言語(SDL) はITUの標準規格であり、遷移の際の以下のような動作を表す記号を定義している。
- イベント送信
- イベント受信
- タイマ開始
- タイマキャンセル
- 別の並行動作するステートマシンを開始
- 判断
SDLには、Abstract Data Types と呼ばれる基本データ型、動作言語、有限状態機械を実行可能にするための実行意味論を埋め込む。
他の状態図
[編集]有限オートマトンには他にも様々な表現方法があり、例えば図3もその一種である。
用途
[編集]ここで示しているような反応性システムの設計だけでなく、有限オートマトンは電気工学、言語学、計算機科学、哲学、生物学、数学、論理学など様々な領域で利用される。有限オートマトンはオートマトン理論や計算理論で研究される一種のオートマトンである。情報工学や計算機科学では、アプリケーションの動作のモデリング、デジタルシステムのハードウェア設計、ソフトウェア工学、コンパイラ設計、通信プロトコルの設計、計算と言語に関する研究などで幅広く活用されている。
分類
[編集]

有限オートマトンは二種類に分類される。アクセプタ / リコグナイザとトランスデューサである。
アクセプタ / リコグナイザ
[編集]このタイプの有限オートマトンは入力を受容(accept)したり、理解(recognize)して、外界に結果を知らせるために状態(state)を使用する。つまり、最終的に受容状態になったかどうかで「はい」または「いいえ」のいずれかを出力として返す。FSMの全状態は受容状態かそうでないかのいずれかである。全入力を処理したとき状態が受容状態なら、その入力は受容されたことになり、さもなくば拒絶 / 却下されたことになる。基本的に入力は記号(または文字)であり、動作(action)は使用されない。図4 に示した例は "nice" という単語を受容する有限オートマトンを示している。この場合、6番だけが受容状態である。
この機械は言語を定義するものとして説明することもできる。その言語とは、その機械が受容する全ての単語から構成され、それ以外の単語を全く含まないもので、そのような言語をその機械が「受容 / 受理」すると称する。定義から、FSM が受理する言語は正規言語であり、逆にある言語を受理する FSM が存在する場合、その言語を正規言語と称する。
初期状態 / 開始状態
[編集]初期状態は、一般にどこからも矢印で指されていない状態である[1]。
受容状態 / 受理状態
[編集]受容状態は、その機械が手続きを成功裡に完了させた状態である。通常、二重丸で表現される。
図5の決定性有限オートマトン (DFA) は2進数の入力が偶数個の 0 を含むときに受容することを示している。S1 は初期状態でもあり、受容状態でもある。この機械は入力数列に"0"が偶数個含まれるときのみ正しく終了したと判定され、0個も偶数なので"0"が全く含まれない数字列も受容される。このDFAが受容する文字列の例としては、ε(空文字列)、1、11、00、010、1010、10110、などなどがある。
トランスデューサ
[編集]

トランスデューサ(変換機、transducer)は、与えられた入力と動作を伴う状態(両方または一方)に基づいて出力を生成する。このタイプの有限オートマトンは計算言語学の分野や制御などに使われる。また、トランスデューサは二種類に分類される。
- ムーア・マシン
- この有限オートマトンは開始動作のみを使用する。すなわち、出力は状態にのみ依存する。ムーア・モデルの利点はふるまいを単純化できることである。図6の例はエレベーターの扉についてのムーア・マシンを示している。この有限オートマトンは「開放命令」と「閉鎖命令」というふたつの命令を理解し、それによって状態が変化する。「開放途中」状態にある開始動作(E:)は扉の開くところを監視し始めることを示し、「閉鎖途中」状態にある開始動作(E:)は扉の閉じるところを監視し始めることを意味する。「開放」と「閉鎖」状態は動作を伴わないが、これらは外界(つまり他のオートマトン)に扉が開いているとか閉まっているといった状況を知らせる意味を持つ。
- ミーリ・マシン
- この有限オートマトンは入力動作のみを使用する。すなわち、出力は入力と状態に依存する。ミーリ・モデルは状態の数を減らす作用がある。図7の例はムーア・マシンの例と同じものをミーリ・マシンで実装したものを示している(実装された有限オートマトンのふるまいは実行モデルに依存する。例えば仮想有限状態機械では動作するが、イベント駆動有限状態機械では動作しない)。これは二つの入力動作を持つ。「閉鎖命令が来たら扉を閉めるためにモーターを起動する」という入力動作と「開放命令が来たら扉を開けるためにモーターを起動する」という入力動作である。
実際には、これらを混合したモデルがよく使用される。
ムーア・モデルとミーリ・モデルの違いの詳細は、実施例も含めて外部サイトの"Moore or Mealy model?"にある(ただし英語)。
決定性
[編集]さらなる分類方法として、決定性有限オートマトン (DFA) と非決定性有限オートマトン (NFA, GNFA) がある。決定性有限オートマトンでは、各状態の考えられる全ての入力について一意に次の状態が決定される。非決定性有限オートマトンでは、ある状態にある入力があったとき遷移がどうなるかが決定されない(遷移がないかもしれないし、複数の遷移が対応しているかもしれない)。このような区別は実行時間などの観点では重要だが、ふるまいに関する観点ではそれほど重要ではない。それぞれのオートマトンで表現可能なふるまいは同じであり、任意のNFAを等価な(しかしより大きな)DFAに変換するアルゴリズムが存在する(冪集合構築)。
ひとつしか状態を持たない有限オートマトンは結合有限オートマトンと呼ばれ、入力動作のみを持つ。これは複数の有限オートマトンが協調動作する場合に便利であり、結合有限オートマトンとして表せる部分を抽出して設計に活用する。
数学モデル
[編集]タイプによって、いくつかの定義が存在する。 アクセプタ有限オートマトンは ⟨Σ, S, s0, δ, F⟩ の5要素から構成される。
- Σ は入力文字セット(有限だが空ではないシンボルの集合)
- S は有限であって空でない状態の集合
- s0 は S の要素でもある初期状態
- δ は状態遷移関数: δ: S × Σ → S (非決定性有限オートマトンの場合、 δ は状態の集合を返すので となる)
- F は終了状態の集合であり、 S の部分集合(空もありうる)
決定性FSMでも非決定性FSMでも は部分関数でもよく、 としたとき、 と のあらゆる組合せについて定義する必要はない。有限オートマトン が という状態で次の入力記号が のとき、 が未定義なら はエラーを返す(すなわち、入力は拒絶・却下される)。これは汎用の状態機械の定義では便利だが、状態機械を変換するのにはあまり便利ではない。デフォルトの形式では全体関数であることを要求するアルゴリズムも存在する。
有限状態機械は制限されたチューリングマシンと見ることもでき、ヘッドが読み取り動作しかできず、常に左から右へと読み取っていくチューリングマシンと言える[2]。
トランスデューサ有限オートマトンは ⟨Σ, Γ, S, s0, δ, ω⟩ の6要素から構成される。
- Σ は入力文字セット(有限だが空ではないシンボルの集合)
- Γ は出力文字セット(有限だが空ではないシンボルの集合)
- S は有限であって空でない状態の集合
- s0 は S の要素でもある初期状態(非決定性有限オートマトンの場合は初期状態の集合)
- δ は状態遷移関数: δ: S × Σ → S
- ω は出力関数
出力関数が状態と入力文字の関数 (ω: S × Σ → Γ ) ならば、その定義はミーリ・モデルであり、ミーリ・マシンとしてモデル化できる。出力関数が状態のみに依存する (ω: S → Γ ) ならば、その定義はムーア・モデルであり、ムーア・マシンとしてモデル化できる。出力機能のない有限オートマトンは状態遷移系などと呼ばれる。
ムーア・マシンの最初の出力シンボル を無視すれば、ミーリ・マシンで遷移ごとに遷移先のムーア・マシンの状態の出力シンボルを出力するよう出力関数を設定すれば、ミーリ・マシンに容易に変換できる。ミーリ・マシンの状態はそこに遷移してくる矢印ごとに異なる出力ラベルが設定されているため、逆の変換はそれほど単純ではない。その場合は、出力シンボルごとに状態を設定してやる必要がある[3]。
最適化
[編集]有限オートマトンの最適化とは、同じ機能を実現するのに必要とされる状態の数をいかに減らすかを意味する。既知の最速のアルゴリズムとして Hopcroft minimization algorithm がある[4][5]。他にも Implication table や Moore reduction procedure といった手法が使われる。また、非環状FSAは線型時間で最小化できる[6]。
実装
[編集]ハードウェアへの適用例
[編集]
デジタル回路では、プログラマブルロジックデバイス、プログラマブルロジックコントローラ、論理ゲート、フリップフロップ、リレーなどを使って有限オートマトンが構成される。もっと具体的に言えば、状態を格納するレジスタを持ち、状態遷移を決定する論理回路と出力を決定する論理回路を持つハードウェアが有限オートマトンであると言える。初期のハードウェア実装として Richards controller がある。
フリップフロップと出力の間には伝播遅延が存在するため、ミーリ・マシンやムーア・マシンからは非同期出力の論理回路が生成される。このため動作周波数が遅くなってしまう。ミーリ・マシンやムーア・マシンはフリップフロップから直接出力する形に変換でき、そうすることで動作周波数を高めることができる。このように変換した有限状態機械を Medvedev FSM と呼ぶことがある[7]。その最も単純な例としてカウンタ回路がある。
ソフトウェアへの適用例
[編集]有限オートマトンを使ったソフトウェアアプリケーションを作るのに以下のコンセプトが一般に使われる。
脚注
[編集]注釈
[編集]出典
[編集]- ^ Sipser 2006, p. 34
- ^ Black, Paul E (12 May 2008). “Finite State Machine”. Dictionary of Algorithms and Data Structures (U.S. National Institute of Standards and Technology).
- ^ James Andrew Anderson; Thomas J. Head (2006). Automata theory with modern applications. Cambridge University Press. pp. 105–108. ISBN 9780521848879
- ^ Hopcroft, John E (1971). An n log n algorithm for minimizing states in a finite automaton[リンク切れ]
- ^ Almeida, Marco; Moreira, Nelma; Reis, Rogerio (2007). On the performance of automata minimization algorithms
- ^ Revuz D. Minimization of Acyclic automata in Linear Time. Theoretical Computer Science 92 (1992) 181-189 181 Elsevier
- ^ “FSM: Medvedev”. 2010年7月10日閲覧。
参考文献
[編集]一般
[編集]- Wagner, F., "Modeling Software with Finite State Machines: A Practical Approach", Auerbach Publications, 2006, ISBN 0-8493-8086-3.
- ITU-T, Recommendation Z.100 Specification and Description Language (SDL)
- Samek, M., Practical Statecharts in C/C++, CMP Books, 2002, ISBN 1-57820-110-1.
- Samek, M., Practical UML Statecharts in C/C++, 2nd Edition, Newnes, 2008, ISBN 0-7506-8706-1.
- Gardner, T., Advanced State Management, 2007
- Cassandras, C., Lafortune, S., "Introduction to Discrete Event Systems". Kluwer, 1999, ISBN 0-7923-8609-4.
- Timothy Kam, Synthesis of Finite State Machines: Functional Optimization. Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9842-4
- Tiziano Villa, Synthesis of Finite State Machines: Logic Optimization. Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9892-0
- Carroll, J., Long, D. , Theory of Finite Automata with an Introduction to Formal Languages. Prentice Hall, Englewood Cliffs, 1989.
- Kohavi, Z., Switching and Finite Automata Theory. McGraw-Hill, 1978.
- Gill, A., Introduction to the Theory of Finite-state Machines. McGraw-Hill, 1962.
- Ginsburg, S., An Introduction to Mathematical Machine Theory. Addison-Wesley, 1962.
理論計算機科学
[編集]- Arbib, Michael A. (1969年). Theories of Abstract Automata (1st ed. ed.). Englewood Cliffs, N.J.: Prentice-Hall, Inc.. ISBN 0-13-913368-2
- Bobrow, Leonard S.; Michael A. Arbib (1974年). Discrete Mathematics: Applied Algebra for Computer and Information Science (1st ed. ed.). Philadelphia: W. B. Saunders Company, Inc.. ISBN 0-7216-1768-9
- Booth, Taylor L. (1967年). Sequential Machines and Automata Theory (1st ed.). New York: John Wiley and Sons, Inc.. Library of Congress Card Catalog Number 67-25924
- Boolos, George; Richard Jeffrey (1989年, 1999年). Computability and Logic (3rd ed. ed.). Cambridge, England: Cambridge University Press. ISBN 0-521-20402-X
- Brookshear, J. Glenn (1989年). Theory of Computation: Formal Languages, Automata, and Complexity. Redwood City, California: Benjamin/Cummings Publish Company, Inc.. ISBN 0-8053-0143-7
- Davis, Martin; Ron Sigal, Elaine J. Weyuker (1994年). Second Edition: Computability, Complexity, and Languages and Logic: Fundamentals of Theoretical Computer Science (2nd ed. ed.). San Diego: Academic Press, Harcourt, Brace & Company. ISBN 0-12-206382-1
- Hopcroft, John; Jeffrey Ullman (1979年). Introduction to Automata Theory, Languages and Computation (1st ed. ed.). Reading Mass: Addison-Wesley. ISBN 0-201-02988-X
- Hopcroft, John E.; Rajeev Motwani, Jeffrey D. Ullman (2001年). Introduction to Automata Theory, Languages, and Computation (2nd ed. ed.). Reading Mass: Addison-Wesley. ISBN 0-201-44124-1
- Hopkin, David; Barbara Moss (1976年). Automata. New York: Elsevier North-Holland. ISBN 0-444-00249-9
- Kozen, Dexter C. (1997). Automata and Computability (1st ed. ed.). New York: Springer-Verlag. ISBN 0-387-94907-0
- Lewis, Harry R.; Christos H. Papadimitriou (1998年). Elements of the Theory of Computation (2nd ed.). Upper Saddle River, New Jersey: Prentice-Hall. ISBN 0-13-262478-8
- Linz, Peter (2006). Formal Languages and Automata (4th ed.). Sudbury, MA: Jones and Bartlett. ISBN 978-0-7637-3798-6
- Minsky, Marvin (1967年). Computation: Finite and Infinite Machines (1st ed.). New Jersey: Prentice-Hall
- Christos Papadimitriou (1993年). Computational Complexity (1st edition ed.). Addison Wesley. ISBN 0-201-53082-1
- Pippenger, Nicholas (1997年). Theories of Computability (1st ed.). Cambridge, England: Cambridge University Press. 0-521-55380-6 (hc)
- Rodger, Susan; Thomas Finley (2006年). JFLAP: An Interactive Formal Languages and Automata Package (1st ed.). Sudbury, MA: Jones and Bartlett. ISBN 0-7637-3834-4
- Sipser, Michael (2006年), Introduction to the Theory of Computation, Second Edition (2nd ed.), Boston Mass: Thomson Course Technology, ISBN 0-534-95097-3
- Wood, Derick (1987年). Theory of Computation (1st ed.). New York: Harper & Row, Publishers, Inc.. ISBN 0-06-047208-1
- Yuri Gurevich (2000), Sequential Abstract State Machines Capture Sequential Algorithms, ACM Transactions on Computational Logic, vl. 1, no. 1 (July 2000), pages 77-111. http://research.microsoft.com/~gurevich/Opera/141.pdf
機械学習
[編集]- Mitchell, Tom M. (1997年). Machine Learning (1st ed.). New York: WCB/McGraw-Hill Corporation. ISBN 0-07-042807-7
回路合成などハードウェアへの応用
[編集]- Booth, Taylor L. (1967年). Sequential Machines and Automata Theory (1st ed.). New York: John Wiley and Sons, Inc.. Library of Congress Card Catalog Number 67-25924
- Booth, Taylor L. (1971年). Digital Networks and Computer Systems (1st ed.). New York: John Wiley and Sons, Inc.. ISBN 0-471-08840-4
- McCluskey, E. J. (1965年). Introduction to the Theory of Switching Circuits (1st ed.). New York: McGraw-Hill Book Company,Inc.. Library of Congress Card Catalog Number 65-17394
- Hill, Fredrick J.; Gerald R. Peterson (1965年). Introduction to the Theory of Switching Circuits (1st ed.). New York: McGraw-Hill Book Company. Library of Congress Card Catalog Number 65-17394
有限マルコフ連鎖プロセス
[編集]- Booth, Taylor L. (1967年). Sequential Machines and Automata Theory (1st ed.). New York: John Wiley and Sons, Inc.. Library of Congress Card Catalog Number 67-25924
- Kemeny, John G.; Hazleton Mirkil, J. Laurie Snell, Gerald L. Thompson (1959年). Finite Mathematical Structures (1st ed.). Englewood Cliffs, N.J.: Prentice-Hall, Inc.. Library of Congress Card Catalog Number 59-12841
関連項目
[編集]- 正規言語 - 有限オートマトンによって表現できる言語のクラス
- 状態遷移系
- オートマトン
- ペトリネット
- シミュレーション
- マービン・ミンスキー
- 状態遷移図
- 隠れマルコフモデル
- 制御システム
- OpenGL
- 人工知能
外部リンク
[編集]- Description from the Free On-Line Dictionary of Computing[リンク切れ]
- NIST Dictionary of Algorithms and Data Structures entry
- Hierarchical State Machines
- Round-trip Engineering State Machines
- SourceForge 状態機械に関するオープンソースのプロジェクト一覧
- A registry of finite-state technology at the IT Center for Science, Finland.


 French
French Deutsch
Deutsch







