等量曲線

等量曲線(とうりょうきょくせん、英: Isoquant)とは、同じ量の財を生産できる2つの生産要素の組を示す曲線(あるいは直線)のこと[1][2]。縦軸と横軸は、それぞれ2つの生産要素の投入量を表す。生産要素とは、多くの場合、労働と資本である。英語をそのまま読んでアイソクォントと記述されることもある。英語で「量」という意味のQuant、とギリシャ語で「等しい」という意味のIsoに由来する。
無差別曲線との比較
[編集]無差別曲線は消費者の効用最大化を理解する上で用いられる。等量曲線は生産者の利潤最大化(あるいは費用最小化)を理解する上で用いられる。
無差別曲線と同様に、2つの等量曲線が交差することはない。図中でより右上に位置している等量曲線はより多い生産量に対応する。
通常は、無差別曲線の位置を比較して、効用水準の違いを定量化することはできない。一方で、等量曲線の場合は生産される財を量的単位で測定することができ、2つの等量曲線を比較してどれくらい生産量が異なるのかを定量的に考察することが可能である。
形状
[編集]

2つの生産要素が代替関係にあり代替の弾力性が無限大ではないとき、等量曲線は図1にあるように曲線の形状となる。生産関数がコブ=ダグラス型であったり、CES型である場合はこのような形状になる。
2つの生産要素が完全代替(Perfect substitute)であるとき、等量曲線は直線になる。これは図2に描かされている。一方の生産要素は同じ量の別の生産要素で代替できる。生産要素が完全代替な場合は、MRTSが変化することがない。
2つの生産要素が完全補完(Perfect complement)である場合、等量曲線は図3にあるように直角に折れ曲がる形状となる。企業は2つの生産要素を常に同一の割合で生産に用いる。
性質
[編集]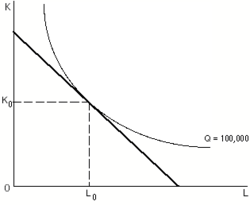
資本と労働の2つの生産要素を用いて財を生産するとする。「資本と労働」の2つの生産要素の投入量を2倍にしたときに、生産量が2倍になるという意味で「規模に関して収穫一定」であるとする。このとき、等量曲線は原点に向かって凸な形状となる。この形状は資本と労働の生産要素の間でトレードオフがあることを意味し、一方の生産要素の投入量を増加させると、限界生産物が低減することを示す。
等量曲線は、技術的限界代替率(Marginal Rate of Technical Substitution, MRTS)の低減によって図では右下がりの形状を持つ[3][4][5]。等量曲線の傾きは、一方の生産要素を別の生産要素に置き換えることができる比率を表します。これは即ちMRTSであり、MRTSはつまり等量曲線の傾きである。したがって、等量曲線の傾きが急であればあるほど、MRTSは大きくなる。 MRTSは減少する必要があるため、等量曲線はその原点に対して凸となる。一方の生産要素の投入量を一定とし、もう一方の生産要素の投入量を増やすと、限界生産物が減少する。
等量曲線が、企業の資源制約線と接しているとき企業は利潤最大化をしている(つまり、最適な資源配分をしている)[6]。その資源制約線の下で、最も多い生産量にあたる等量曲線上で生産することが即ち利潤最大化であるからである。そこでは、等量曲線は資源制約線と接しているはずである。
複数の等量曲線を描くことで、例えば2つの等量曲線の間の距離を測ることで、生産量の変化を測ることができる。生産量が増加するにつれてこれらの等量曲線の間の距離が縮小する場合、企業の生産関数は「規模に関して収穫逓減」であることになる。逆に、生産量が増加するにつれて等量曲線間の距離が拡大していく場合は、企業の生産関数は「規模に関して収穫逓増」であることになる。
等量曲線は最適な資源配分を理解する上で用いることができる。等量曲線を見れば、企業が、同じ生産量を生産するのに必要な、複数の生産要素の組を知ることができる。したがって、利潤最大化(あるいは費用最小化)を実現する上で利用できる[7] 。
費用最小化は、「限界生産物の比率」が「要素価格の比率」に等しいときに実現できる。このとき、等量曲線の傾きと「等費用曲線」の傾きは等しくなる(図4の接点を参照のこと)。ここでは、生産に必要な費用を最小限に抑えられているため、企業は費用最小化を実現する点で生産する誘因を持つ[8]。
非凸の等量曲線
[編集]
MRTSが低減する場合は、等量曲線は原点に向かって凸になる。少なくとも1つの生産要素の で規模に関して収穫逓増がある場合、局所的に非凸の等量曲線が発生する場合がある。この場合、代替の弾力性が負になる。つまり、生産要素Aと生産要素Bの比率が増加するにつれて、「生産要素Bの限界生産物(Marginal product)」に対する「生産要素Aの限界生産物」の比率は減少するのではなく増加する。
非凸な等量曲線を持つ場合は、価格変化に応じた生産要素の投入を最小限に抑えるために、価格の変化に対して不連続な投入の調整をすることがある。
例えば、等量曲線が全体的に非凸で、等費用曲線が線形である場合を考える。この場合、生産要素の最小費用の組は端点解(Corner solution)となり、2つのうち1つの生産要素のみ生産に用いられる。どちらの生産要素を用いるかは、生産要素の相対価格によって決まる。相対価格のわずかな変化に応じて、最適な生産要素の投入は、「生産要素Aのみをすべて用いる」から「生産要素Bのみをすべて用いる」に変化したり、またその逆に変化したりする。
出典
[編集]- ^ Varian, Hal R. (1992). Microeconomic Analysis (Third ed.). Norton. ISBN 0-393-95735-7
- ^ Chiang, Alpha C. (1984). Fundamental Methods of Mathematical Economics (Third ed.). McGraw-Hill. pp. 359–363. ISBN 0-07-010813-7
- ^ “Efficient Combination of Labor and Capital”. www2.econ.iastate.edu. 2021年4月25日閲覧。
- ^ “Isoquants”. www.economics.utoronto.ca. 2021年4月25日閲覧。
- ^ “Production Functions”. UCLA (n.d.). 25 April 2021閲覧。
- ^ Arrow, K. J.; Chenery, H. B.; Minhas, B. S.; Solow, R. M. (1961). “Capital-Labor Substitution and Economic Efficiency”. The Review of Economics and Statistics 43 (3): 225–250. doi:10.2307/1927286. ISSN 0034-6535. JSTOR 1927286.
- ^ “The Discovery of the Isoquant” (英語). ResearchGate. 2021年4月25日閲覧。
- ^ “Expansion path, ridgeline and least cost combination of inputs”. Eagri (n.d.). 2021年4月25日閲覧。


 French
French Deutsch
Deutsch