木構造 (データ構造)

木構造(きこうぞう)とは、グラフ理論における木に対応づけられるデータ構造である。
用語
[編集]木構造は、一般のグラフ構造と同様の、ノード(節点、頂点)とノード間を結ぶエッジ(枝、辺)あるいはリンクで表すこともできるが、木構造専用の、特に有向の根付き木となるような表現が使われることも多い。
データ構造として使われる木は、ほとんどの場合、根となるノードが決められた根付き木である。さらに、有向木であることも多い。[注 1]
ノード間の関係は家系図に見立てた用語で表現される。木構造内の各ノードは、0個以上の子ノード (英: child node) を持ち、子ノードは木構造内では下方に存在する(木構造の成長方向は下とするのが一般的である)。子ノードを持つノードは、子ノードから見れば親ノード (英: parent node) である。あるノードから見て、同じ親を持つノードを兄弟ノード (英: sibling node) という。あるノードから見て、その子ノードやそこから先の子ノード全てのいずれかを子孫ノード (英: descendant node) と呼び、その親ノードやそこから先の親ノードの全てのいずれかを先祖ノード (英: ancestor node) と呼ぶ。ノードは高々1個の親ノードを持つ。
根ノード (英: root node) とは、親ノードを持たないノードのこと。根ノードは木構造の最上位にあるノードであり、1つの木構造に高々1つしか存在しない。根ノードからスタートして、親から子へ、またその子へ、とエッジを辿っていくと、あらゆるノードへ必ず到達でき、そのような(根から特定ノードまでの)経路は常に一意である。図で示す場合、根ノードが一番上に描かれるのが普通である。二分ヒープなどの木構造では、根ノードは特別な属性を持つ。木構造内の全てのノードは、そのノードを頂点とする部分木の根ノードと見なすことができる。
葉ノード (英: leaf node) とは、子ノードを持たないノードのこと。葉ノードは木構造の下位の末端にあるノードであり、ひとつの木に複数存在しうる。
内部ノード (英: internal node、inner node) とは、子ノードを持つノード、すなわち葉ノード以外のノードのこと。
高さ (英: height) とは、あるノードについて、そのノードからその子孫である葉ノードへのエッジ数の最大値のこと。 根ノードの高さはその木構造の高さである。
深さ (英: depth) とは、逆に、あるノードについて、そのノードから根ノードまでのエッジ数のこと。根ノードの深さは 0 である。
部分木 (英: subtree) は、木構造の一部であり、それ自身も完全な木構造となっている部分を指す。木構造 T の任意のノードは、その配下の全ノードと共に T の部分木を構成する。根ノードを頂点とする部分木は、その木構造全体と等しい。根ノード以外を頂点とする部分木は真部分木 (英: proper subtree) と呼ばれる(部分集合と真部分集合とのアナロジー)。
森 (英: forest) とは、木の集合のこと。グラフ理論では、森は閉路をもたない(連結とは限らない)グラフである。 森が順序木の順序集合である場合、これを木の木と考えることで前順、間順、後順の走査法を再帰的に定義できる。
子ノードの順序性
[編集]あるノードの子ノード群の間に順序が存在しない木と、順序が存在する木がある。順序性のある木を実装するには、子ノードをリストに入れたり、各エッジ(枝)に異なる自然数を付与するなどして子ノード間に順序を入れる。これが順序付き木 (英: ordered tree) である。順序付き木の応用としては2分探索木などがある。コンピュータ中のデータ構造としては、順序が存在しないデータ構造といったものは(セット型のように存在はするが)あまり一般的ではないため、普通の実装では自然に順序付き木となる。
実装方法
[編集]コンピュータで利用する場合にはいくつかの実装方法がある。典型的な実装としては、動的メモリ確保でノードを表す構造体の領域を確保し、ポインタで親ノードや子ノードを参照できるようにする。
- 各ノードが子ノードへのポインタのリストを持つ
- 各ノードが親ノードへのポインタを持つ
- 各ノードが親ノードへのポインタと子ノードへのポインタのリストを持つ
- 各ノードが長男ノードへのポインタと弟ノードへのポインタを持つ
他にも、配列を使った実装(ポインタではなく、インデックスによって親子関係が決定される)などがある(例えば、二分ヒープ)。
走査法
[編集]



木構造の走査 (英: traverse) とは、木構造にある全ノードを一回ずつ体系的に調査する処理である。連結リストや1次元の配列のような線形性のあるデータ構造では、走査は普通は前から順番に行われる(後ろからたどる方法などもある)。木構造の走査には下記の方法などがある。以下のアルゴリズムは二分木に関するものだが、多分木にも応用可能である。
深さ優先探索
[編集]深さ優先探索は、現在のノードを調査し、その子ノードに対して同じことを繰り返す。従って、再帰呼び出しで容易に表現できる(ループでも実装可能)。走査法は、ノードを調査する順序によって以下の3つに分類される(いずれの方法も、根から探索を開始する)。
- 前順・先行順・前置順・行きがけ順 (英: pre-order)
-
- 根ノードを調査する。
- もしあれば、左の部分木を前順走査する。
- もしあれば、右の部分木を前順走査する。
- 2分探索木のコピーを作る際によく利用される。また、数式の構文木からポーランド記法の表現を得るのにも利用される。
- 間順・中間順・通りがけ順 (英: in-order)
-
- もしあれば、左の部分木を間順走査する。
- 根ノードを調査する。
- もしあれば、右の部分木を間順走査する。
- 多分木では定義されない。2分探索木では、間順走査によって走査する順がソートされた順序になるため、よく使われる。
- 後順・後行順・後置順・帰りがけ順 (英: post-order)
-
- もしあれば、左の部分木を後順走査する。
- もしあれば、右の部分木を後順走査する。
- 根ノードを調査する。
幅優先探索
[編集]走査例
[編集]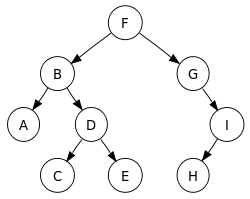 | この2分探索木において、
|
擬似コード
[編集]前順(n) n を処理 for each (n の子ノード i) 前順(i)
間順(n) if (n に左の子ノードがあれば) 間順(n の左の子ノード) n を処理 if (n に右の子ノードがあれば) 間順(n の右の子ノード)
後順(n) for each (n の子ノード i) 後順(i) n を処理
これらの実装では、木構造の高さのぶんだけコールスタック領域を必要とする。平衡が保たれていない木では、これが深刻な問題となる場合もある。各ノードの親ノードの位置を覚えておくことでスタックを使わないようにもできる。
下記はレベル順の擬似コード。
レベル順(n) n をキューに追加 while (キューに要素を含むなら) n ← キューから取り出す n を処理 for each (n の子ノード i) i をキューに追加
糸付き2分木
[編集]
また、糸付き2分木 (英: threaded binary tree) を使う方法もある。Joseph M. Morris が1979年に発表した[1]。糸付き2分木は、子ノードがない場合に間順の前と後ろをそれぞれ左の子ポインタと右の子ポインタに設定しておいた木構造である。この場合、子ノードの有無はポインタ以外のフィールドで示す必要がある。これを使うと、間順走査の効率が非常によくなるが、前順や後順は通常のスタックを使った実装の方がよい。
糸付き2分木を間順走査するコードは次のようになる。
Sub inorder(n∈node) Do While hasLeftChild(n) Let node ← node.left Loop Do visit(n) If hasRightChild(n) Then Let n ← n.right Do While hasLeftChild(n) Let n ← n.left Loop Else Let n ← n.right End If Loop While n ≠ Null End Sub 主な操作
[編集]- アイテム(データを持つノード)数を数え上げる。
- あるアイテムを探索する。
- 新たなアイテムを木構造の特定の位置に追加する。
- アイテムを削除する。
- 部分木を削除する(枝刈り)
- 部分木を追加する(接ぎ木)
- 任意のノードから根ノードを探す。
木構造の種類
[編集]コンピュータにみる木構造
[編集]木構造は主に以下のような用途で使われる
- 階層構造のあるデータを操作する。ディレクトリツリー、ドメイン名、構文木、制御構造、決定木、XML DOMツリーなど。
- 情報を探索しやすくする。データベースのインデックス など。この用途の木構造を探索木とも呼ぶ。
- データのソートのために使用する。ヒープソートなど。
脚注
[編集]注釈
[編集]- ^ 一般に無向木は、それに含まれる任意のノードを根として解釈可能な非根付き木である。有向木は、エッジが、葉から根に向かう向きの場合と、根から葉に向う向きの場合があるが、いずれにしても根となるノードが決められた根付き木となる。
出典
[編集]- ^ Morris, Joseph M. (December 1979). “Traversing binary trees simply and cheaply”. Information Processing Letters 9 (5): 197-200. doi:10.1016/0020-0190(79)90068-1.
関連項目
[編集]参考文献
[編集]- Donald Knuth. The Art of Computer Programming: Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89683-4 . Section 2.3: Trees, pp.308–423.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7 . Section 10.4: Representing rooted trees, pp.214–217. Chapters 12–14 (Binary Search Trees, Red-Black Trees, Augmenting Data Structures), pp.253–320.
- Dale, Nell. Lilly, Susan D. "Pascal Plus Data Structures". D. C. Heath and Company. Lexington, MA. 1995. Fourth Edition.
- Drozdek, Adam. "Data Structures and Algorithms in C++". Brook/Cole. Pacific Grove, CA. 2001. Second edition.
外部リンク
[編集]- Description from the Dictionary of Algorithms and Data Structures
- List of data structures from LEDA
- Storing Hierarchical Data in a Database PHP による走査コード例がある
- Working with Graphs in MySQL
- Animation Applet of Binary Tree Traversal
- discmath_dvi:8.4. Tree Transversal


 French
French Deutsch
Deutsch