正則グラフ

正則グラフ（せいそくグラフ、英: regular graph）は、グラフ理論において、各頂点の隣接する頂点数が全て同じであるようなグラフである。すなわち、全ての頂点の次数が等しい。頂点の次数が k の正則グラフを「k-正則グラフ」または「次数 k の正則グラフ」と呼ぶ。

次数2までの正則グラフの分類は容易である。0-正則グラフは連結されていない頂点で構成され、1-正則グラフは連結されていない辺で構成され、2-正則グラフは連結されていない閉路で構成される。

3-正則グラフは立方体グラフとも呼ばれる。

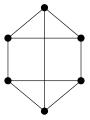
正則グラフのうち、隣接する2つの頂点に共通する隣接点が常に同じ l 個で、隣接しない2つの頂点に共通する隣接点が常に同じ n 個となっているものを強正則グラフという。正則だが強正則でない最小のグラフは、6頂点の閉路グラフかつ循環グラフである。

完全グラフ $K_{m}$ は任意の $m$ について強正則である。

クリスピン・ナッシュ＝ウィリアムズの定理によれば、2k+1 個の頂点から成る k-正則グラフには必ずハミルトン路がある。

0-正則グラフ
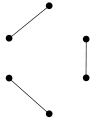
1-正則グラフ
2-正則グラフ
3-正則グラフ

代数的属性

あるグラフの隣接行列を A とする。そのグラフが k-正則であることは、ベクトル ${\textbf {j}}=(1,\dots ,1)$ が固有値 k に属する A の固有ベクトルであることと同値である^[1]。他の固有値に対応した固有ベクトルは ${\textbf {j}}$ と直交なので、そのような固有ベクトル $v=(v_{1},\dots ,v_{n})$ について $\sum _{i=1}^{n}v_{i}=0$ が成り立つ。

次数 k の正則グラフが連結していることと、固有値 k の重複度が1であることは同値である^[1]。

正則な連結グラフの判定基準も存在する。グラフが連結かつ正則であることと、 $J_{ij}=1$ である行列 J がそのグラフの隣接代数（Aの冪乗の1次結合）にあることは同値である。^[要出典]

グラフGはk-正則グラフで、直径D、隣接行列の固有値群は $k=\lambda _{0}>\lambda _{1}\geq \dots \geq \lambda _{n-1}$ とする。Gが2部グラフでないなら、次が成り立つ。

$D\leq {\frac {\log {(n-1)}}{\log(k/\lambda )}}+1$

ここで $\lambda =\max _{i>0}\{\mid \lambda _{i}\mid \}$ である。^[要出典]

生成

正則グラフを生成するソフトウェアとして GenReg がある^[2]。

脚注・出典

^ ^a ^b Cvetković, D. M.; Doob, M.; and Sachs, H. Spectra of Graphs: Theory and Applications, 3rd rev. enl. ed. New York: Wiley, 1998.
^ Regular Graphs M. Meringer, J. Graph Theory, 1999, 30, 137.

外部リンク

Weisstein, Eric W. "Regular Graph". mathworld.wolfram.com (英語).
Weisstein, Eric W. "Strongly Regular Graph". mathworld.wolfram.com (英語).
GenReg software and data by Markus Meringer.
Nash-Williams, Crispin (1969), “Valency Sequences which force graphs to have Hamiltonian Circuits”, University of Waterloo Research Report, Waterloo, Ontario: University of Waterloo

[Cvetkovic-1] Cvetković, D. M.; Doob, M.; and Sachs, H. Spectra of Graphs: Theory and Applications, 3rd rev. enl. ed. New York: Wiley, 1998.

[2] Regular Graphs M. Meringer, J. Graph Theory, 1999, 30, 137.

[1]

[2]

表話編歴グラフ理論
要素・定義・表現	頂点辺（英語版）グラフ無向有向ラベル付き（英語版）重み付き（英語版）ハイパーグラフ接続行列隣接行列隣接リスト
指標	位数（英語版）サイズ（英語版）次数次数行列距離（英語版）半径直径内周 (頂点)彩色数辺彩色数（英語版）点連結度辺連結度交叉数（英語版）
部分構造	ループ（英語版）多重辺（英語版）部分グラフ（英語版）誘導部分グラフ道閉道連結成分（英語版）強連結成分（英語版）橋（英語版）カットクリーク独立集合支配集合（英語版）マッチングオイラー路シュタイナー木全域木ハミルトン路
全体構造	連結グラフ正則グラフ立方体グラフケージ強正則グラフ木平面グラフ 2部グラフ有向非巡回グラフ弦グラフムーアグラフパーフェクトグラフ対称グラフ半対称グラフ頂点推移グラフ辺推移グラフ距離推移グラフ補グラフ双対グラフグラフ同型
固有名を持つグラフ	パスグラフ（英語版） $P n$ 閉路グラフ $C n$ 完全グラフ $K n$ 完全2部グラフ $K m, n$ スター $S n = K 1, n$ 車輪グラフ $W n$ 空グラフピーターセングラフヒーウッドグラフマギーグラフホフマンシングルトングラフフォークマングラフ
トピック・定理	一筆書きオイラーの多面体定理クラトフスキの定理四色定理五色定理ケイリーの公式プリューファー列最短経路問題巡回セールスマン問題中国人郵便配達問題ダイクストラ法ベルマン-フォード法ワーシャル-フロイド法ハミルトン閉路問題最大クリーク問題頂点被覆問題最小頂点被覆問題最大独立集合問題最大流最小カット定理支配集合問題次数直径問題安定結婚問題
カテゴリ / コモンズ

正則グラフ

代数的属性

生成

脚注・出典

関連項目

外部リンク