Granica Tolmana-Oppenheimera-Volkoffa – Wikipedia, wolna encyklopedia
Granica Tolmana-Oppenheimera-Volkoffa (granica TOV, limit TOV) – maksymalna możliwa masa stabilnej sferycznie symetrycznej i nierotującej gwiazdy neutronowej, wynikająca z Ogólnej Teorii Względności.
Historia
[edytuj | edytuj kod]Metoda obliczenia masy maksymalnej poprzez rozwiązanie równań Einsteina dla sferycznie symetrycznego rozkładu masy (równanie Tolmana-Oppenheimera-Volkoffa) zostało opublikowane w roku 1939 w czasopiśmie naukowym „Physical Review” przez Richarda C. Tolmana w artykule pt. Static Solutions of Einstein’s Field Equations for Spheres of Fluid[1] oraz Roberta Oppenheimera i Georga M. Volkoffa w artykule pt. On Massive Neutron Cores[2] (obie prace ukazały się w tym samym woluminie; Tolman pracował niezależnie od Oppenheimera i Volkoffa, jednak przed publikacją dyskutowali o otrzymanych wynikach).
Znaczenie w astrofizyce i fizyce jądrowej
[edytuj | edytuj kod]Dla danego równania stanu, sferycznie symetryczna gwiazda neutronowa o masie większej niż wartość graniczna TOV staje się niestabilna względem sferycznie-symetrycznych zaburzeń: arbitralnie małe zaburzenie wytrąca konfigurację ze stanu równowagi, powodując zapadnięcie się jej do osobliwości, czyli przekształcenie gwiazdy w czarną dziurę Schwarzschilda (co może sugerować, że granica TOV jest jednocześnie minimalną masą astrofizycznej czarnej dziury). Granica TOV istnieje dla każdego równania stanu, także dla materii nieściśliwej (tzn. takiej w której gęstość ρ=const.) i materii kwarkowej.
Oryginalna wartość maksymalnej masy gwiazdy neutronowej według Oppenheimera i Volkoffa wynosiła około 0,7 masy Słońca. Wartość ta wynikała z ówczesnego stanu wiedzy na temat materii o tak dużej gęstości – do obliczeń wykorzystano równania stanu zimnego zdegenerowanego gazu Fermiego neutronów – i, jak wskazują obserwacje astronomiczne i rozwój teorii oddziaływań jądrowych, jest ona mocno niedoszacowana. Obecnie wiadomo, że ciśnienie zapewniające stabilność gwiazdy neutronowej o masie porównywalnej z masą Słońca nie pochodzi od gazu Fermiego neutronów, ale jest efektem oddziaływań silnych pomiędzy nukleonami. Dokładne pomiary mas pulsarów w relatywistycznych układach podwójnych znajdują się w przedziale od 1,25[3] do 2,01[4] M☉. Niektóre modele teoretyczne dopuszczały dla statycznej gwiazdy neutronowej maksymalną masę równą nawet 3 M☉[5][6].
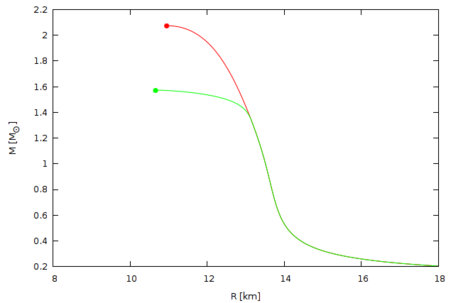
Równanie stanu materii dla gęstości większych od gęstości jądrowej jest wciąż niedokładnie zbadane, dlatego znajomość maksymalnej możliwej masy gwiazdy neutronowej jest istotna z punktu widzenia weryfikacji teorii budowy gęstej materii. Równanie stanu jest wykluczone przez obserwacje, jeżeli otrzymana dla niego granica TOV jest niższa od największej masy statycznej gwiazdy neutronowej obserwowanej w przyrodzie; np. obserwacja gwiazdy neutronowej o masie 1,8 masy Słońca wyklucza zasadność używania równania stanu, którego wykres oznaczono na rysunku kolorem zielonym, natomiast to oznaczone kolorem czerwonym nie kłóci się z tą obserwacją.
Równoczesna obserwacja w 2017 roku fal grawitacyjnych i promieniowania elektromagnetycznego z kilonowej, w połączeniu z opisem teoretycznym, pozwoliła nałożyć silne ograniczenie na maksymalną masę nierotującej gwiazdy neutronowej. Według obliczeń badaczy z Uniwersytetu Goethego jest ona nie większa niż ~2,16 M☉[9][10][11].
Zobacz też
[edytuj | edytuj kod]Przypisy
[edytuj | edytuj kod]- ↑ R.C. Tolman. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. „Phys. Rev.”. 55, s. 364–373, 1939. DOI: 10.1103/PhysRev.55.364.
- ↑ J.R. Oppenheimer, G.M. Volkoff. On Massive Neutron Cores. „Phys. Rev.”. 55, s. 374–381, 1939. DOI: 10.1103/PhysRev.55.374.
- ↑ Duncan R. Lorimer. Binary and Millisecond Pulsars. „Living Reviews in Relativity”. 11 (8), 2008. DOI: 10.12942/lrr-2008-8. Bibcode: 2008LRR....11....8L.
- ↑ John Antoniadis, Paulo C.C. Freire, Norbert Wex, Thomas M. Tauris i inni. A Massive Pulsar in a Compact Relativistic Binary. „Science”. 340 (6131), 2013. DOI: 10.1126/science.1233232. (ang.).
- ↑ C.E. Rhoades, R. Ruffini. Maximum Mass of a Neutron Star. „Phys. Rev. Lett.”. 32, s. 324, 1974. DOI: 10.1103/PhysRevLett.32.324.
- ↑ Vassiliki Kalogera, Gordon Baym. The Maximum Mass of a Neutron Star. „Astrophysical Journal Letters”. 470, s. L61, 1996. DOI: 10.1086/310296.
- ↑ N.K. Glendenning, J. Schaffner-Bielich. First order kaon condensate. „Phys. Rev. C”. 025803. 60, 1999. [UKlin=-100 MeV].
- ↑ J. Zimanyi, S.A. Moszkowski. Nuclear Equation of state with derivative scalar coupling. „Physical Review C”. 42 (4), s. 1416–1421, 1990. DOI: 10.1103/PhysRevC.42.1416. (ang.).
- ↑ Luciano Rezzolla, Elias R. Most, Lukas R. Weih. Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. „The Astrophysical Journal Letters”. 852 (2), 2018. DOI: 10.3847/2041-8213/aaa401. (ang.).
- ↑ How massive can neutron stars be?. Uniwersytet Johanna Wolfganga Goethego we Frankfurcie nad Menem, 2018-01-15. [dostęp 2018-01-19]. (ang.).
- ↑ Agnieszka Nowak: Jak masywne mogą być gwiazdy neutronowe?. Urania – Postępy Astronomii, 2018-01-17. [dostęp 2018-01-19]. (pol.).


 French
French Deutsch
Deutsch

