Gráfico – Wikipédia, a enciclopédia livre

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências (Encontre fontes: ABW  • CAPES  • Google (notícias • livros • acadêmico)). (Abril de 2017)

Gráfico é a tentativa de se expressar visualmente dados ou valores numéricos, de maneiras diferentes, assim facilitando a sua compreensão.^[1] Existem vários tipos de gráficos e os mais utilizados são os de colunas, os de linhas e os circulares. Os principais elementos são: números, título, fonte, nota e chamada.

O gráfico de colunas é composto por duas linhas ou eixos, um vertical e outro horizontal. No eixo horizontal são construídas as colunas que representam a variação de um fenômeno ou de um processo de acordo com sua intensidade. Essa intensidade é indicada pelo eixo vertical. As colunas devem sempre possuir a mesma largura e a distância entre elas deve ser constante.

Ver artigo principal: Histograma

É parecido com o gráfico de colunas em vários aspectos, pois sua construção é praticamente igual, mas seu cálculo é feito pela área do retângulo representado no gráfico. Geralmente não apresenta escala vertical, somente o eixo horizontal que representa a variável analisada. A área pode ser calculada em porcentagem. O gráfico é utilizado para amostras grandes e variáveis numéricas.

Os gráficos de setor são representados por círculos divididos proporcionalmente de acordo com os dados do fenômeno ou do processo a ser representado. Os valores são expressos em números ou em percentuais (%).

O gráfico de linha é composto por dois eixos, um vertical e outro horizontal, e por uma linha que mostra a evolução de um fenômeno ou processo.

Os gráficos de barras são muito usados para comparar quantidades. As barras podem aparecer na vertical ou na horizontal, quando também são chamadas de colunas. Seja na horizontal ou na vertical, quanto maior o comprimento de uma barra, maior o valor que representa. Quanto menor o comprimento de uma barra menos valor ela tem. A não ser que esteja representando números negativos, esta regra é aplicável.

Partes divididas entre um círculo ou quadrado. Ex: tipo de população marcada escolhida usado em pesquisa

Um gráfico de área enfatiza a magnitude da alteração ao longo do tempo. As séries são exibidas como um conjunto de pontos conectados por uma linha, com uma área preenchida abaixo da linha. Os valores são representados pela altura do ponto medida pelo eixo y. Os rótulos de categoria são exibidos no eixo x. Os gráficos de área geralmente são usados para comparar valores ao longo do tempo.

Um gráfico de rosca ilustra a relação entre as partes e um todo; entretanto, ele pode conter mais de uma série. Os dados de valor são exibidos como porcentagem do todo. As categorias são representadas por fatias individuais. Os gráficos de rosca são usados geralmente para mostrar porcentagens. Eles são funcionalmente idênticos aos gráficos de pizza.

Um gráfico de radar, também conhecido como gráfico de aranha ou gráfico de estrela devido à sua aparência, plota os valores de cada categoria ao longo de um eixo separado que inicia no centro do gráfico e termina no anel externo.

Eixo cartesiano bidimensional são duas retas orientadas (normalmente referidas como eixos das abscissas e ordenadas), perpendiculares entre si, onde se representam as coordenadas correspondentes às variáveis independentes e dependentes de uma função. As variáveis independentes são aquelas às quais atribuímos valores. As variáveis dependentes, como o próprio nome indica, têm valores que dependem daqueles atribuídos às variáveis independentes.

Os valores da variável independente da função ficam no eixo das abscissas, enquanto os valores da variável dependente são colocados no eixo das ordenadas, por convenção. A cada par de valores, correspondente um ponto e a figura formada por esses pontos é a “curva” da função. Se essa “curva” for uma reta, por exemplo, a função é chamada de linear.

O gráfico de uma função ${\displaystyle f:D\to I}$ é o conjunto dos pares ordenados em ${\displaystyle D\times I}$ da forma ${\displaystyle \left(x,f(x)\right),}$ ou seja:

${\displaystyle \left\{\left(x,f(x)\right):x\in D\right\}}$

ou equivalentemente:

${\displaystyle \left\{\left(x,y\right)\in D\times I:x\in D{\mbox{ e }}y=f(x)\right\}}$

os termos deste par ordenado são chamados de abcissa e ordenada.

Uma função é determinada pelo seu gráfico e pela especificação do conjunto de chegada. Assim, se duas funções têm o mesmo gráfico, uma poderá ser sobrejectiva e a outra não. No entanto, a injectividade de uma função é completamente determinada pelo gráfico.

Embora o conceito de gráfico esteja relacionado ao conceito de desenho, pode-se falar do gráfico de funções em espaços de dimensão infinita. Um importante teorema da análise funcional é o teorema do gráfico fechado.

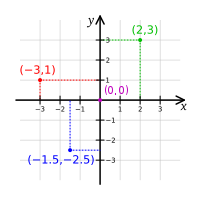
Uma das aplicações mais corriqueiras da ideia de gráfico de uma função é o traçado de uma curva sobre o plano cartesiano de forma a explicitar as "principais" propriedades de uma função.

O gráfico de muitas funções reais específicas recebem nomes especiais. O gráfico de um função afim, ou polinômio do primeiro grau, é chamado de reta; de um polinômio do segundo grau, de parábola; de um polinômio do terceiro grau, de parábola cúbica; da função ${\displaystyle y=\cosh(x)}$ é uma catenária.

${\displaystyle y=f(x)}$ no intervalo [-10 10 -10 10]:

• 
  ${\displaystyle x}$ (função identidade)
• 
  ${\displaystyle |x|}$
• 
  ${\displaystyle \mathrm {sen} \,x}$
• 
  ${\displaystyle \cos x}$
• 
  ${\displaystyle \csc x}$
• 
  ${\displaystyle \sec x}$
• 
  ${\displaystyle \tan x}$
• 
  ${\displaystyle \cot x}$
• 
  ${\displaystyle \exp x}$
• 
  ${\displaystyle 2^{-x}}$
• 
  Logaritmos em várias bases
• 
  ${\displaystyle {\sqrt {10-x^{2}}}}$
• 
  ${\displaystyle {\sqrt {x}}}$
• 
  ${\displaystyle x^{2}}$
• 
  ${\displaystyle x^{3}}$

Referências

• Portal da matemática