Rombidodecadodecaedru complex

Descriere
Rombicosidodecaedru complex

Tip	compus poliedric uniform degenerat
Fețe	54 (30 pătrate, 12 pentagoane, 12 pentagrame)
Laturi (muchii)	120
Vârfuri	20
χ	−46
Configurația vârfului	3(5/3.4.5.4)^[1]
Diagramă Coxeter
Grup de simetrie	Compus: icosaedrică (I_h, [5,3], 532) Constituenți: icosaedrică (I_h*)
Poliedru dual	rombicosidodecacron complex
Proprietăți	Constituenți: 1 dodecadodecaedru ditrigonal, 1 compus de cinci cuburi

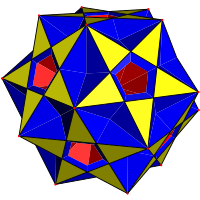
În geometrie rombicosidodecaedrul complex este un compus poliedric uniform degenerat, având 54 de fețe (30 de pătrate, 12 pentagoane și 12 pentagrame), 120 de laturi (dublate) și 20 de vârfuri.^[2] Fețele formate din câte două muchii suprapuse sunt considerate din punct de vedere topologic fețe.

În fiecare vârf se întâlnesc câte douăsprezece fețe: câte trei pentagoane și trei pentagrame, care formează fațetele triunghiulare externe, și câte șase pătrate, care formează fețele interne.

Văzut drept compus

Rombicosidodecaedrul complex poate fi văzut ca un compus format dintr-un dodecadodecaedru ditrigonal și un compus de cinci cuburi,^[1] cu muchiile lor contopindu-se, în ele întâlnindu-se câte 4 fețe. Rombicosidodecaedrui complex seamănă cu un dodecadodecaedru ditrigonal, deoarece compusul de cinci cuburi este conținut complet în interiorul dodecadodecaedrului ditrigonal.

Compus poliedric

Dodecadodecaedru ditrigonal	Compus de cinci cuburi	Compusul

Mărimi asociate

Coordonate carteziene

Având în comun vârfurile cu dodecadodecaedrul ditrigonal, coordonatele carteziene ale vârfurilor compusului cu lungimea laturii 2, centrat în origine, sunt toate permutările ale:^[3]^[4]

\left(\,\pm 1,\,\pm 1,\,\pm 1\,\right)

\left(\,\pm \varphi ,\,\pm (\varphi -1),\,0\,\right)

unde $\varphi ={\frac {1+{\sqrt {5}}}{2}}$ este secțiunea de aur.

Raza sferei circumscrise

Raza sferei circumscrise este și ea egală cu raza dodecadodecaedrului ditrigonal. Pentru lungimea laturii egală cu $a$ , ea este:^[1]^[5]

R={\frac {\sqrt {3}}{2}}\,a\approx 0,866025\,a.

Note

^ ^a ^b ^c en Klitzing, Richard. „3D uniform polyhedra”. Cheie: cadditradid
^ en Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), „Uniform polyhedra”, Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246 (916): 401–450, Bibcode:1954RSPTA.246..401C, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446 (Table 6, degenerate cases)
^ en Coxeter, H.S.M. Regular Polytopes (third edition), Dover Publications Inc, 1973 ISBN: 0-486-61480-8, p. 52, §3.7 Coordinates for the vertices of the regular and quasi-regular solids
^ en Eric W. Weisstein, Icosahedral group la MathWorld.
^ en Eric W. Weisstein, Ditrigonal Dodecadodecahedron la MathWorld.

Vezi și

Portal Matematică

[K-1] Klitzing, Richard. „3D uniform polyhedra”. Cheie: cadditradid

[2] Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), „Uniform polyhedra”, Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246 (916): 401–450, Bibcode:1954RSPTA.246..401C, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446 (Table 6, degenerate cases)

[3] Coxeter, H.S.M. Regular Polytopes (third edition), Dover Publications Inc, 1973 ISBN: 0-486-61480-8, p. 52, §3.7 Coordinates for the vertices of the regular and quasi-regular solids

[4] Eric W. Weisstein, Icosahedral group la MathWorld.

[5] Eric W. Weisstein, Ditrigonal Dodecadodecahedron la MathWorld.

[1]

[2]

[3]

[4]

[5]