Runcinare
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici. |

În geometrie runcinarea este o operație care taie un politop regulat (sau fagure) simultan de-a lungul fețelor, laturilor și vârfurilor, creând fațete noi în locul centrelor fețelor, laturilor și vârfurilor inițiale.
Este o operațiune de trunchiere de ordin superior, asemănătoare cu cantelarea și trunchierea.
Este notată cu simbolul Schläfli extins t0,3{p,q,...}. Operația se poate aplica doar 4-politopurilor, {p,q,r}, sau politopurilor superioare.
Pentru politopuri uniforme și faguri tridimensionali uniformi convecși operația este dual simetrică.
Pentru un 4-politop regulat {p,q,r}, celulele inițiale {p,q} rămân, dar devin separate. Golurile de la fețele separate devin prisme p-gonale. Golurile dintre fețele separate devin prisme r-gonale. Golurile dintre vârfurile separate devin celule {r,q}. Figura vârfului pentru un 4-politop regulat {p,q,r} este o antiprismă q-gonală (numită antipodium dacă p și r sunt diferite).
Pentru 4-politopuri regulate sau faguri regulați această operație a fost denumită de către Alicia Boole Stott expandare, așa cum este imaginată prin mutarea celulelor formei regulate mai departe de centru și completarea cu noile fețe a golurilor apărute la fiecare vârf și latură.
Forme runcinate de 4-politopuri/faguri:
| Simbol Schläfli Diagramă Coxeter | Nume | Figura vârfului | Imagine |
|---|---|---|---|
| 4-politopuri uniforme | |||
| t0,3{3,3,3} | 5-celule runcinat |  |  |
| t0,3{3,3,4} | 16-celule runcinat (Același cu 8-celule runcinat) |  |   |
| t0,3{3,4,3} | 24-celule runcinat |  |  |
| t0,3{3,3,5} | 120-celule runcinat (Același cu 600-celule runcinat) |  |  |
| Faguri euclidieni uniformi convecși | |||
| t0,3{4,3,4} | Fagure cubic runcinat (Același cu fagure cubic) | 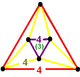 |  |
| Faguri hiperbolici uniformi convecși | |||
| t0,3{4,3,5} | Fagure cubic de ordinul 5 runcinat |  | |
| t0,3{3,5,3} | Fagure icosaedric runcinat | 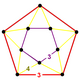 | |
| t0,3{5,3,5} | Fagure dodecaedric de ordinul 5 runcinat |  | |
Bibliografie
[modificare | modificare sursă]- en Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN: 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation, p 210 Expansion)
- en Norman Johnson, Uniform Polytopes, Manuscript (1991)
- en Norman Johnson, The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- en John Horton Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 26)
Vezi și
[modificare | modificare sursă]Legături externe
[modificare | modificare sursă]- en Eric W. Weisstein, Expansion la MathWorld.


 French
French Deutsch
Deutsch