Подера — Википедия

Поде́ра (фр. podaire, от др.-греч. πούς, род. пад. ποδός — нога[1][2], то есть стопа перпендикуляра; англ. pedal curve; pedal) кривой относительно точки — некоторая кривая, составленная из оснований перпендикуляров, опущенных из данной точки на касательные к данной кривой[2][3][4][5][6][7][8].
Устаревший термин подэ́ра[3][9][10], или подэ́рная крива́я[9].
В некоторых математических текстах вместо русского термина «подера» используется калька с английского «педаль»[11][12].
Например, подера окружности относительно точки, лежащей не в центре окружности, — это улитка Паскаля[3][13].
Подера кривой есть инверсия полярного преобразования кривой, полюсы которых совпадают с полюсом подеры[14].
Впервые подера рассмотрена 30 июня 1718 года Колином Маклореном (англ. Colin Maclaurin), профессором математики из Абердина, в журнале Философские труды Королевского общества (англ. Philosophical Transactions of the Royal Society) в статье на латинском языке «III. Трактат о построении и измерении кривых, где большинство бесконечных серий кривых сводятся либо к прямым линиям, либо к более простым кривым. Автор Колин Маклорен, профессор математики в колледже[англ.] Нового Абердина[англ.]» (лат. III. Tractatus de Curvarum Constructione et Mensura; ubi plurimae Series Curvarum Infinitae vel rectis mensurantur vel ad Simpliciores Curvas reducuntur. Autore Colin Maclaurin, in Collegio novo Abredonensi Matheseos Professore)[15][16][17].
Определения
[править | править код]Определения подеры и антиподеры на плоскости
[править | править код]Поде́ра, или (первая) позитивная подера[18][19], или подошвенная кривая[19] (англ. pedal; pedal curve; first positive pedal), кривой — некоторая кривая, составленная из оснований перпендикуляров, опущенных из фиксированной точки, которая называется полюсом[6][20][8], или центром[4], или точкой подеры[20][21], на касательные к исходной кривой[3][2][4][5][6][7][21][20][8]. Подера кривой порядка , , имеет порядок [6].
Устаревший термин подэ́ра[3][9][10], или подэ́рная крива́я[9].
В некоторых математических текстах вместо русского термина «подера» используется калька с английского «педаль»[11][12].

Антиподе́ра, или (первая) негативная подера[22][23][19] (англ. first negative pedal), кривой относительно точки — кривая, подера которой относительно той же точки есть исходная кривая[3][2][19]. Другими словами, антиподера — огибающая кривая перпендикуляров, проведённых через точки исходной кривой к прямым, соединяющим точки исходной кривой с фиксированной точкой — полюсом[23].
Например, парабола есть антиподера прямой, если полюс антиподеры совпадает с фокусом параболы[6][19], как показано на рисунке справа.
Построение антиподеры исходя из уже построенной её подеры называется построением с помощью подеры[9].
Например, всегда получится коническое сечение, если осуществить построение с помощью подеры из окружности или прямой[9][19].
Поде́ры степене́й вы́ше пе́рвой обеих разновидностей определяются как подеры подер предыдущей степени с одним и тем же полюсом[23].
- Подеры кубики Чирнгауза и антиподеры секстики Кэли шести степеней
- Прямая — 2-я подера кубики Чирнгауза, парабола — 5-я антиподера секстики Кэли
- Точка — 3-я подера кубики Чирнгауза, прямая — 4-я антиподера секстики Кэли
- Окружность — 4-я подера кубики Чирнгауза, точка — 3-я антиподера секстики Кэли
- Кардиоида — 5-я подера кубики Чирнгауза, окружность — 2-я антиподера секстики Кэли
- Секстика Кэли — 6-я подера кубики Чирнгауза, кардиоида — 1-я антиподера секстики Кэли
Определение подеры через инверсию и полярное преобразование
[править | править код]
Имеет место схема преобразований кривых для подеры, инверсии и полярного преобразования кривой, показанная на рисунке справа, из которой вытекает следующее утверждение[14]:
- подера кривой есть инверсия полярного преобразования кривой, окружности преобразования которых совпадают, а полюсы совпадают с полюсом подеры.
Другие связанные определения
[править | править код]Поде́рное преобразова́ние — преобразование плоскости, отображающее точки каждой кривой в соответствующие точки её подеры. Это преобразование неточечное, то есть оно не сохраняет точки, прямые и окружности[4]. Подерное преобразование есть касательное преобразование (преобразование Ли)[24].
Поде́рная систе́ма координа́т — система координат, основанная на подерном преобразовании и состоящие из двух величин: расстояний от полюса до точки кривой и до соответствующей точки её подеры[25][26].
Поде́ра пове́рхности, или подерная поверхность[27] — некоторая поверхность, составленная из оснований перпендикуляров, опущенных из постоянной точки на касательные плоскости данной поверхности[3][27].
Подо́ида, или втори́чная ка́устика (англ. orthotomic; orthotomic curve; secondary caustic), кривой относительно данного полюса — кривая, получающаяся из подеры растяжением в два раза относительно полюса[28][29]. Другими словами, подоида — некоторая кривая, составленная из точек, симметричных полюсу относительно касательных данной кривой[30][29][31]. Эволюта ортотомики есть каустика[31].
В некоторых математических текстах вместо русского термина «подоида» используется калька с английского «ортото́мика»[11].
Например, подоида конического сечения относительно его фокуса есть[32]:
- окружность с центром в другом фокусе эллипса или гиперболы;
- директриса параболы.
Антиподо́ида кривой относительно полюса — кривая, подоида которой относительно полюса есть исходная кривая[33]. Другими словами, антиподоида — огибающая кривая перпендикуляров, проведённых через середины отрезков, соединяющих точки исходной кривой с полюсом[33].
Контраподе́ра[34][35], или норма́льная поде́ра, или норма́льная поде́рная кри́вая (англ. contrapedal; normal pedal; normal pedal curve), кривой относительно полюса — подера эволюты этой кривой относительно того же полюса. Другими словами, котраподера — некоторая кривая, составленная из оснований перпендикуляров, опущенных из полюса на нормали данной кривой[18][34][35]. Соответственно, подера кривой относительно полюса — это контраподера эвольвенты этой кривой относительно того же полюса[35]
Уравнения подеры
[править | править код]Параметрические уравнения подеры
[править | править код]Параметрические уравнения подеры на вещественной плоскости
[править | править код]В общем случае, для параметрически заданной кривой , имеющей производную , подера
относительно точки задаётся следующими уравнениями[36][21]:
Эти основные уравнения[37] можно принять за определение подеры[38].
Параметрическое уравнение касательной прямой параметрически заданной кривой , имеющей производную , в точке , имеет вид
Параметрическое уравнение прямой перпендикулярной касательной и параллельной нормали к параметрически заданной кривой , имеющей производную , в точке , имеет вид
Если эта перпендикулярная прямая проходит через точку , то она имеет вид
Чтобы найти точку пересечения касательной прямой и прямой, перпендикулярной к ней и проходящей через точку , нужно решить систему уравнений
Вычтем из левой и правой частей первого равнения соответственно левую и правую части второго:
Подставим полученное выражение для в первое уравнение системы уравнений:
Иногда основные уравнения записывают в более сложном виде[38]:
В частном случае, относительно полюса в начале координат, основные уравнения будут такими[3][36]:
Параметрические уравнения подеры в двумерном векторном пространстве
[править | править код]В векторном виде основное уравнение будет проще[38]:
или в более сложном виде[38]:
где — вектор нормали, перпендикулярный касательной[38].
Относительно полюса [38][3][36]:
или в более сложном виде[38][3][36]:
Параметрические уравнения подеры на комплексной плоскости
[править | править код]В комплексных числах для параметрически заданной кривой , имеющей производную , основное уравнение подеры
относительно точки будут ещё проще[40][37]:
В частном случае, относительно полюса , основное уравнение будет таким[40][37]:

Найдём основное уравнение подеры кривой относительно полюса в начале координат , показанном на рисунке справа вместе с вещественной осью . Текущая точка кривой — , подеры — .
Из треугольника получаем модуль функции :
Так как радиус-вектор составляет с вещественной осью угол , то аргумент комплексной функции равен
Тогда искомое уравнение
Заменим комплексную функцию синуса, используя формулу Эйлера:
Снова используем одну из показательных форм комплексного числа
- и
окончательно получим:
Параметрические уравнения подеры в вещественном пространстве
[править | править код]Для параметрически заданной пространственной кривой , имеющей производную , подера относительно точки задаётся следующими уравнениями[3]:
Прямоугольная система координат
[править | править код]Для кривой с неявным уравнением , имеющей частные производные и подера относительно точки задаётся следующими параметрическими уравнениями[41]:
Для поверхности с неявным уравнением , имеющей частные производные , и , подера относительно точки задаётся следующими параметрическими уравнениями[3]:
Подерная система координат
[править | править код]Самое простое уравнение подеры получается в подерной системе координат. Для кривой, имеющей подерное уравнение
- или
относительно некоторого полюса, подерное уравнение её подеры
- или
относительно того же полюса[42]
В соответствии с утверждения о пропорциональности подерных координат, радиальное и перпендикулярное расстояния исходной кривой относительно некоторого полюса пропорциональны соответствующим расстояниям её подеры относительно того же полюса:
- или
Отсюда получаем:
или
или
Примеры подеры
[править | править код]Подера окружности
[править | править код]Подера окружности с полюсом в центре есть та же самая окружность. Подера окружности с полюсом вне центра есть улитка Паскаля, в частности, если полюс подеры лежит на самой окружности, то подера — кардиоида[4].
- Подеры окружности
- Гиперболическая улитка Паскаля — полюс подеры вне окружности
- Кардиоида — полюс подеры на окружности
- Эллиптическая улитка Паскаля — полюс подеры внутри окружности, но не в её центре
Найдём уравнение подеры окружности. Уравнение окружности в комплексном параметрическом виде
где — постоянный комплексный центр окружности; — постоянный вещественный радиус окружности; — вещественный параметр. Получаем:
и уравнение подеры окружности с полюсом , то есть улитки Паскаля[37]:
Уравнение улитки Паскаля упростится, если прямая параллельна вещественной оси комплексной плоскости, то есть или
Рассмотрим два частных случая подеры[37]:
- если и совпадают, то есть подера окружности есть сама окружность с центром в начале координат — полюсе подеры:
- если лежит на окружности, то есть имеем уравнение кардиоиды с центром в каспе — полюсе подеры:
- если при этом прямая параллельна вещественной оси комплексной плоскости, то есть или то уравнение кардиоиды
- а если при этом окружность имеет радиус и слева от , то самое простое уравнение кардиоиды
Подера параболы
[править | править код]
Любая парабола имеет подеру — циркулярную кривую 3-го порядка на комплексной проективной плоскости[6].
Не умаляя общности, уравнение произвольной параболы можно записать в следующем виде[6]:
- или
где — расстояние от фокуса параболы до её вершины и от вершины до директрисы.
Тогда подера произвольной параболы относительно произвольного полюса есть дефективная гипербола с двойной точкой , асимптотой и следующим уравнением[6]:
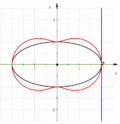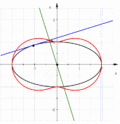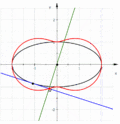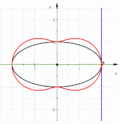
Подера эллипса
[править | править код]Подера эллипса
- относительно его фокуса — окружность,
- относительно центра эллипса — лемниската Бута.
- Подеры эллипса
- Окружность — полюс подеры в фокусе эллипса
- Лемниската Бута — полюс подеры в центре эллипса. Здесь a=2 b=1, уравнение 4x2+y2=(x2+y2)2
См. также
[править | править код]Примечания
[править | править код]- ↑ Подера, 1988.
- ↑ 1 2 3 4 Подера и антиподера, 1975.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 Иванов А. Б. Подера, 1984.
- ↑ 1 2 3 4 5 Яглом И. М., Атанасян Л. С. Геометрические преобразования, 1963, 8.4. Подерное преобразование, с. 134.
- ↑ 1 2 Савелов А. А. Плоские кривые, 1960, 8. Рациональные циркулярные кривые, с. 63.
- ↑ 1 2 3 4 5 6 7 8 Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, с. 64.
- ↑ 1 2 Коренцова М. М. Колин Маклорен. 1698—1746, 1998, Знакомство с Ньютоном. Абердин, с. 13. Органическое описание кривых, с. 131.
- ↑ 1 2 3 Ferréol Robert. Pedal of a Curve, 2017.
- ↑ 1 2 3 4 5 6 Гильберт Д., Кон-Фоссен С. Наглядная геометрия, 1981, с. 33.
- ↑ 1 2 Савелов А. А. Плоские кривые, 1960, 1. Подэры, с. 282.
- ↑ 1 2 3 Брус Дж., Джиблин П. Кривые и особенности, 1988, 1. Педальная кривая, с. 48—49. 5.32. Ортотомические, педальные и двойственные кривые, с. 114—116.
- ↑ 1 2 Подерный (педальный) треугольник, 2004—….
- ↑ Яглом И. М., Атанасян Л. С. Геометрические преобразования, 1963, 8.4. Подерное преобразование, с. 134—135.
- ↑ 1 2 Zwikker C. The Advanced Geometry of Plane Curves and Their Applications, 1963, Chapter XI. Pedals and other derived curves, p. 152.
- ↑ Maclaurin C. III. Tractatus de Curvarum Constructione et Mensura…, 1718.
- ↑ Article. III. Tractatus de Curvarum Constructione et Mensura…, 2024.
- ↑ Коренцова М. М. Колин Маклорен. 1698—1746, 1998, Знакомство с Ньютоном. Абердин, с. 11—12.
- ↑ 1 2 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 2.4. Pedal Curves (Maclaurin, 1718), p. 46.
- ↑ 1 2 3 4 5 6 Коренцова М. М. Колин Маклорен. 1698—1746, 1998, Органическое описание кривых, с. 131.
- ↑ 1 2 3 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 2; 2.4. Pedal Curves (Maclaurin, 1718), p. 46.
- ↑ 1 2 3 Weisstein Eric W. Pedal Curve, 2024.
- ↑ Савелов А. А. Плоские кривые, 1960, 2. Негативные подэры, с. 284.
- ↑ 1 2 3 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 2.4. Pedal curves, p. 46.
- ↑ Яглом И. М., Атанасян Л. С. Геометрические преобразования, 1963, 8.4. Подерное преобразование, с. 136.
- ↑ Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 2.
- ↑ Брус Дж., Джиблин П. Кривые и особенности, 1988, 7.21. Упражнения. 6, с. 176—177.
- ↑ 1 2 Брус Дж., Джиблин П. Кривые и особенности, 1988, Простые особенности, с. 236.
- ↑ Савелов А. А. Плоские кривые, 1960, 3. Подоиды, с. 285.
- ↑ 1 2 Брус Дж., Джиблин П. Кривые и особенности, 1988, 5.32. Ортотомические, педальные и двойственные кривые, с. 114.
- ↑ Савелов А. А. Плоские кривые, 1960, 3. Подоиды, с. 284—285.
- ↑ 1 2 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 2.10. Caustic (Tschirnhausen, Huygens, 1680), p. 60.
- ↑ Брус Дж., Джиблин П. Кривые и особенности, 1988, 7.21. Упражнения. 5, с. 176.
- ↑ 1 2 Брус Дж., Джиблин П. Кривые и особенности, 1988, 7.14. Упражнения. 2. Антиортотомики, с. 161.
- ↑ 1 2 Alfred Gray. Modern differential geometry of curves and surfaces with Mathematica, 2006, 4.7 Exercises. 16, p. 117.
- ↑ 1 2 3 Zwikker C. The Advanced Geometry of Plane Curves and Their Applications, 1963, Chapter XI. Pedals and other derived curves, p. 151.
- ↑ 1 2 3 4 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 2.4. Pedal curves, p. 49.
- ↑ 1 2 3 4 5 6 Zwikker C. The Advanced Geometry of Plane Curves and Their Applications, 1963, Chapter XI. Pedals and other derived curves, p. 150.
- ↑ 1 2 3 4 5 6 7 Alfred Gray. Modern differential geometry of curves and surfaces with Mathematica, 2006, 4.6 Pedal Curves, p. 113.
- ↑ 1 2 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 2.4. Pedal curves, p. 48—49.
- ↑ 1 2 Alfred Gray. Modern differential geometry of curves and surfaces with Mathematica, 2006, 4.7 Exercises. 15, p. 117.
- ↑ Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве, 1997.
- ↑ Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 49.
Источники
[править | править код]- Брус Дж., Джиблин П.[англ.] Кривые и особенности: Геометрическое введение в теорию особенностей: Пер. с англ. И. Г. Щербак под ред. В. И. Арнольда. М.: Мир, 1988. 262 с. (Современная математика. Вводные курсы) ISBN 5-03-001194-3. [J. William Bruce, Peter G. Giblin. Curves and Singularities. A geometrical introduction to singularity theory. Cambridge: Cambridge University Press, 1984.]
- Гильберт Д., Кон-Фоссен С. Наглядная геометрия: Пер. с нем. С. А. Каменецкого. 3-е изд. М.: Наука, 1981. 144 с.
- Иванов А. Б. Подера // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 4 Ок—Сло. М.: «Советская энциклопедия», 1984. 1216 стб. Стб. 370.
- Коренцова М. М. Колин Маклорен. 1698—1746. М.: Наука, 1998. 144 с. (Научно-биографическая литература.) ISBN 5-02-003691-9.
- Подера // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с. С. 465.
- Подера и антиподера // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1975. Т. 20. Плата — проб. 1975. 608 с. С. 109.
- Подерный (педальный) треугольник // Задачи. Проект МЦНМО при участии школы 57, 2004—…. Архивная копия от 2 октября 2023 на Wayback Machine
- Савелов А. А. Плоские кривые. Систематика, свойства, применения. (Справочное руководство) / Под ред. А. П. Нордена. М.: Физматлит, 1960. 293 с.
- Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка. М.: Физматлит, 1961. 271 с.
- Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве. Справочник с приложенипем дискеты «Плоские кривые». М.: ФАЗИС, 1997. 334 с. ISBN 5-7036-0027-8.
- Яглом И. М., Атанасян Л. С. Геометрические преобразования // Энциклопедия элементарной математики, книга четвёртая — геометрия / Гл. ред. П. С. Александров, А. И. Маркушевич, А. Я. Хинчин. Ред. книги 4: В. Г. Болтянский, И. М. Яглом. М.: Физматгиз, 1963. 568 с. С. 49—158.
- Article. III. Tractatus de Curvarum Constructione et Mensura…. 2024 // ROYAL SOCIETY PUBLISHING. Philosophical Transactions. Архивная копия от 25 октября 2019 на Wayback Machine
- Ferréol Robert. Pedal of a Curve // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 10 апреля 2023 на Wayback Machine
- Alfred Gray. Modern differential geometry of curves and surfaces with Mathematica. Third Edition by Elsa Abbena and Simon Salamon. Studies in Advanced Mathematics: Chapman and Hall/CRC, 2006. 982 p.
- Lawrence J. D. A Catalog of Special Plane Curves. New York: Dover Publications, Inc., 1972. 218 p.
- Maclaurin C. III. Tractatus de Curvarum Constructione et Mensura; ubi plurimae Series Curvarum Infinitae vel rectis mensurantur vel ad Simpliciores Curvas reducuntur. Autore Colin Maclaurin, in Collegio novo Abredonensi Matheseos Professore // Philosophical Transactions of the Royal Society. 30 June 1718. Volume 30, Issue 356. P. 803–812.
- Weisstein Eric W. Pedal Curve // Wolfram MathWorld Архивная копия от 5 декабря 2022 на Wayback Machine
- Zwikker C.[англ.] The Advanced Geometry of Plane Curves and Their Applications[англ.]The Advanced Geometry of Plane Curves and Their Applications. New York: Dover Publications, Inc., 1963. 299 p. ISBN 0486610780. ISBN 9780486610788.


 French
French Deutsch
Deutsch


![Парабола — 1-я подера кубики Чирнгауза — 6-я антиподера секстики Кэли[англ.]](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e7/Parabola_is_pedal_of_Tschirnhausen_cubic.svg/120px-Parabola_is_pedal_of_Tschirnhausen_cubic.svg.png)







=\mathbf {Z} (t)=(X(t),\;Y(t))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e62b6ffd30ac4f64f7f742cb042f08bf3c7b6235)



























=\mathbf {Z} (t)=\mathbf {z} (t)-\mathbf {z} '(t){\frac {(\mathbf {z} (t)-\mathbf {z} _{0})\mathbf {z} '(t)}{|\mathbf {z} '(t)|^{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2ad8a27b27f8540b8ad95c929575a359bbab5d9)
=\mathbf {Z} (t)=\mathbf {z} _{0}+\mathbf {z} '_{\bot }(t){\frac {(\mathbf {z} (t)-\mathbf {z} _{0})\mathbf {z} '_{\bot }(t)}{|\mathbf {z} '(t)|^{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/845f135e247d52d6a707a69a3f76eb208b15b79c)


=\mathbf {Z} (t)=\mathbf {z} (t)-\mathbf {z} '(t){\frac {\mathbf {z} (t)\mathbf {z} '(t)}{|\mathbf {z} '(t)|^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac9f90f45d1b4e0139634233d74e45133efb4a4d)
=\mathbf {Z} (t)=\mathbf {z} '_{\bot }(t){\frac {\mathbf {z} (t)\mathbf {z} '_{\bot }(t)}{|\mathbf {z} '(t)|^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de1bfdfa1077a603dd9914dfb6bad6292fe94c9c)


=Z(t)=(X(t),\;iY(t))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7931a2ef18cea0d02248f887fe39c4a170c0e83c)

=Z(t)={\frac {(z(t)-z_{0}){\overline {z'(t)}}-{\overline {z(t)-z_{0}}}z'(t)}{2{\overline {z'(t)}}}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d101e46ef5636a28d6651a7dce782e6b6702c557)

=Z(t)={\frac {z(t){\overline {z'(t)}}-{\overline {z(t)}}z'(t)}{2{\overline {z'(t)}}}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a95674234a07597520e9634dab914181dc68b224)