Гомотопия — Википедия

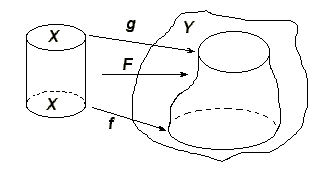
Гомото́пия — семейство непрерывных отображений ${\displaystyle F_{t}\colon X\to Y,\;t\in [0,1]}$, непрерывно зависящих от параметра, более точно — непрерывное отображение ${\displaystyle F\colon [0,1]\times X\to Y}$.

• Отображения ${\displaystyle f,g\colon X\to Y}$ называются гомотопными (${\displaystyle g\sim f}$), если существует гомотопия ${\displaystyle f_{t}}$ такая, что ${\displaystyle f_{0}=f}$ и ${\displaystyle f_{1}=g}$.
  • Это задаёт отношение эквивалентности между непрерывными отображениями ${\displaystyle X\to Y}$.

• Гомотопическая эквивалентность топологических пространств ${\displaystyle X}$ и ${\displaystyle Y}$ — пара непрерывных отображений ${\displaystyle f\colon X\to Y}$ и ${\displaystyle g\colon Y\to X}$ такая, что ${\displaystyle f\circ g\sim \operatorname {id} _{Y}}$ и ${\displaystyle g\circ f\sim \operatorname {id} _{X}}$, здесь ${\displaystyle \sim }$ обозначает гомотопность отображений. В этом случае также говорят, что ${\displaystyle X}$ с ${\displaystyle Y}$ имеют один гомотопический тип.
  • Если ${\displaystyle X}$ и ${\displaystyle Y}$ гомеоморфны (${\displaystyle X\simeq Y}$), то они гомотопически эквивалентны; обратное в общем случае неверно.

• Гомотопический инвариант — характеристика пространства, которая сохраняется при гомотопической эквивалентности топологических пространств; то есть если два пространства гомотопически эквиваленты, то они имеют одинаковую характеристику. Например: связность, фундаментальная группа, эйлерова характеристика.
• Если на некотором подмножестве ${\displaystyle A\subset X,\;F(t,a)=f(a)}$ для всех ${\displaystyle t}$ при ${\displaystyle a\in A}$, то ${\displaystyle F}$ называется гомотопией относительно ${\displaystyle A}$, а ${\displaystyle f}$ и ${\displaystyle g}$ — гомотопными относительно ${\displaystyle A}$.
• Отображение, гомотопное постоянному, то есть отображению в точку, называют стягиваемым, или гомотопным нулю.

• Изотопия — гомотопия топологического пространства ${\displaystyle X}$ по топологическому пространству ${\displaystyle Y}$ ${\displaystyle f_{t}\colon X\to Y,\;t\in [0,1]}$, в которой при любом ${\displaystyle t}$ отображение ${\displaystyle f_{t}}$ является гомеоморфизмом ${\displaystyle X}$ на ${\displaystyle f_{t}(X)\subset Y}$.
• Отображение ${\displaystyle f\colon X\to Y}$ называется слабой гомотопической эквивалентностью, если оно индуцирует изоморфизм гомотопических групп. Подпространство ${\displaystyle A}$ топологического пространства ${\displaystyle X}$ такое, что включение ${\displaystyle A\subset X}$ является слабой гомотопической эквивалентностью, называется репрезентативным подпространством.
• Если ${\displaystyle \varphi :E\to X}$ и ${\displaystyle \varphi ':E'\to X}$ есть произвольные расслоения над ${\displaystyle X,}$ то гомотопия ${\displaystyle f_{t}:E\to E'}$ называется послойной, если ${\displaystyle \varphi 'f_{t}=\varphi .}$ Морфизмы ${\displaystyle f,g:E\to E'}$ послойно гомотопны, если существует послойная гомотопия ${\displaystyle f_{t}:E\to E',}$ для которой выполняются равенства ${\displaystyle f_{0}=f}$ и ${\displaystyle f_{1}=g.}$ Морфизм ${\displaystyle f:E\to E'}$ — послойная гомотопическая эквивалентность, если существует морфизм ${\displaystyle g:E'\to E}$ такой, что ${\displaystyle gf}$ и ${\displaystyle fg}$ послойно гомотопны ${\displaystyle \mathrm {Id} .}$ Расслоения ${\displaystyle E}$ и ${\displaystyle E'}$ принадлежат к одному и тому же послойному гомотопическому типу, если существует хотя бы одна послойная эквивалентность ${\displaystyle f:E\to E'.}$

• Гомотопические группы
• Фундаментальная группа
• Цепная гомотопия

• Васильев В. А. Введение в топологию. — М.: ФАЗИС, 1997. — 132 с. — ISBN 5-7036-0036-7.
• Рохлин В. А., Фукс Д. Б. Начальный курс топологии. Геометрические главы. — М.: Наука, 1977
• Спеньер Э. Алгебраическая топология. — М.: Мир, 1971

Это заготовка статьи по математике. Помогите Википедии, дополнив её.