Бутстрепова агрегація — Вікіпедія

Частина з циклу
Машинне навчання та добування даних
Парадигми Кероване навчання Некероване навчання Інтерактивне навчання Пакетне навчання Метанавчання Напівкероване навчання Самокероване навчання Навчання з підкріпленням Навчання на основі правил Квантове машинне навчання
Задачі Класифікація Породжувальна модель Регресія Кластерування Знижування розмірності Оцінювання густини Виявляння аномалій Очищування даних[en] АвтоМН Асоціативні правила Семантичний аналіз[en] Структурове передбачування Конструювання ознак Навчання ознак Навчання ранжуванню Виведення граматик[en] Навчання онтологій[en] Мультимодальне навчання[en]
Кероване навчання (класифікація • регресія) Ансамблі Випадковий ліс Бутстрепова агрегація Підсилювання Градієнтне підсилювання[en] AdaBoost[en] Дерева рішень MARS[en] CART Доречно-векторна машина k-сусідів Лінійна регресія Логістична регресія Лінійний розділювальний аналіз Наївний баєсів класифікатор Перцептрон Підмайстрове навчання Опорно-векторна машина Штучні нейронні мережі
Кластерування BIRCH[en] CURE Ієрархічне k-середніх Нечітке Очікування-максимізація DBSCAN OPTICS Спектральне Зсув середнього[en]
Знижування розмірності Факторний аналіз Метод незалежних компонент[en] Канонічна кореляція Дискримінантний аналіз Метод головних компонент Власний узагальнений розклад[en] Розклад невід'ємних матриць t-розподілене вкладення стохастичної близькості Навчання розріджених словників[en]
Структурове передбачування Графові моделі Баєсова мережа Прихована марковська модель Умовне випадкове поле
Виявляння аномалій RANSAC k-НС Коефіцієнт локального відхилення Відстань Кука Ізоляційний ліс[en]
Штучна нейронна мережа Автокодувальник Когнітивні обчислення[en] Глибоке навчання DeepDream Нейронна мережа прямого поширення Рекурентна нейронна мережа ДКЧП ВРВ МВС Резервуарне обчислення Обмежена машина Больцмана ГЗМ Дифузійна модель Самоорганізаційна карта Згорткова нейронна мережа U-Net Трансформер Зоровий Спайкова нейронна мережа[en] Мемтранзистор Електрохімічна ПДД[en] (ECRAM)
Навчання з підкріпленням Q-навчання SARSA Метод часових різниць Багатоагентне навчання з підкріпленням Гра проти себе[en]
Навчання з людьми Активне навчання (машинне навчання)[en] Краудсорсинг Людина-в-циклі
Діагностування моделей Крива спроможності навчатися[en]
Математичні засади Ядрові машини Компроміс зсуву та дисперсії Ймовірнісно приблизно коректне навчання Мінімізація емпіричного ризику Оккамове навчання[en] Регуляризація LASSO[en] Тихонова Еластично-сіткова[en] Статистичне навчання Теорія Вапника — Червоненкіса Теорія обчислювального навчання[en]
Місця машинного навчання ECML PKDD[en] NeurIPS[en] ICML[en] ICLR IJCAI ML JMLR
Пов'язані статті Глосарій штучного інтелекту[en] Список наборів даних для досліджень з машинного навчання Перелік понять машинного навчання[en]
п о р

Бутстрепова агрегація або беггінг^[1] (англ. Bootstrap aggregating, bagging) — це машинний навчальний груповий мета-алгоритм, створений для покращення стабільності і точності машинних навчальних алгоритмів, які використовують статистичні класифікації і регресії. Він також зменшує неточність, хоча зазвичай застосовується до методів «дерева рішень», але може використовуватися з будь-яким типом методів.

Метод схожий на ансамбль методів однак, замість використання декількох моделей на одних і тих самих даних, кожна модель застосовується до різних вибірок отриманих методом бутстреп. ^[2]

Наприклад, дано стандартний навчальний набір D розміром n. Даний мета-алгоритм сукупності створює нові навчальні зразки ${\displaystyle D_{i}}$, відбираючи однорідно або із заміною зразки з набору D , кожен з яких розміром nʹ. Деякі спостереження можуть повторюватися в кожному ${\displaystyle D_{i}}$. Якщо n′=n, тоді для великого n набір ${\displaystyle D_{i}}$ очікувано матиме дріб (1 — 1/e) (≈63.2 %) єдиних прикладів D, а всі інші будуть дублюватися. Такий вид відбору відомий як бутстреп відбір.

Сумування приводить до «покращення нестійких процедур» (Брейман, 1996), які включають, наприклад, штучні нервові системи, класифікаційні і регресивні дерева та відбір підгрупи в лінійній регресії (Брейман, 1996). Цікаве застосування алгоритму показано тут.^[3][4] Алгоритм трішки понижує значення стійких методів таких як К-найближчі сусіди (Брейман, 1996).

Щоб проілюструвати основні принципи бутстрепу, нижче показано аналіз відношення між озоном і температурою (дані з Rousseeuw and Leroy (1986), доступно в класичних наборах даних, аналіз робиться в R (мова програмування).

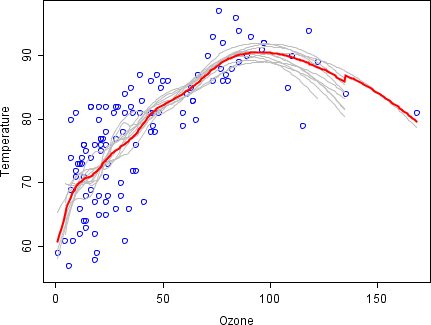
Взаємозв'язок між озоном і температурою в цьому прикладі є очевидно нелінійним, що видно на розсіяному графіку. Щоб описати математично це відношення застосовують LOESS рівні частинки. Замість того, щоб побудувати одну точку з повним набором даних, зразу намалювали 100 зразків за аналогією. Кожен зразок відрізняється від початкового набору даних, але він схожий за розподілом і мінливістю. Прогноз був зроблений на основі 100 груп. Перші 10 прогнозованих зразків є сірими лініями на графіку, які є дуже гнучкими.

Беручи середнє число із 100 зразків, кожний з них встановлює підгрупу початкових даних, ми підходимо до одного сукупного прогнозованого — це червона лінія на графіку:

Похибка одного найближчого сусіднього класифікатора є вдвічі більшою за похибку баєсового класифікатора.^[5] За допомогою уважного вибору розміру зразків сукупність сумування цих зразків може привести до помітного покращення 1NN класифікатора. Беручи велику кількість зразків розміром ${\displaystyle n'}$, супутній найближчий класифікатор буде послідовним, забезпечуючи ${\displaystyle n'\to \infty }$ та відходячи від норми, але ${\displaystyle n'/n\to 0}$ як відібраний розмір ${\displaystyle n\to \infty }$.

Під безконечною симуляцією сукупний найближчий сусідній класифікатор може розглядатися як масовий найближчий сусідній класифікатор. Допускаємо, що характерний простір є ${\displaystyle d}$ вимірним і позначається ${\displaystyle C_{n,n'}^{bnn}}$, сукупний найближчий класифікатор базується на навчальному наборі розміром ${\displaystyle n}$ та зі зразком розміром ${\displaystyle n'}$. У безконечному відборі зразків за певних регулярних умов на групових розподілах крайня похибка має наступну формулу^[6]

${\displaystyle {\mathcal {R}}_{\mathcal {R}}(C_{n,n'}^{bnn})-{\mathcal {R}}_{\mathcal {R}}(C^{Bayes})=\left(B_{1}{\frac {n'}{n}}+B_{2}{\frac {1}{(n')^{4/d}}}\right)\{1+o(1)\},}$

для деяких констант ${\displaystyle B_{1}}$ and ${\displaystyle B_{2}}$. Оптимальний вибір nʹ, що збалансовує два терміни, є у формулі ${\displaystyle n'=Bn^{d/(d+4)}}$ для деякої константи ${\displaystyle B}$.

Бутстрепову агрегацію запропонував 1944 року Лео Брейман для покращення класифікації випадково утворених наборів даних. See Breiman, 1994. Technical Report No. 421.

• Підсилювання (машинне навчання)
• Статистичний бутстреп
• Перехресне затверджування
• Random forest
• Random subspace method (attribute bagging)

• Breiman, Leo (1996). Bagging predictors. Machine Learning. 24 (2): 123—140. doi:10.1007/BF00058655. CiteSeerX: 10.1.1.121.7654.

• Alfaro, E., Gámez, M. and García, N. (2012). adabag: An R package for classification with AdaBoost.M1, AdaBoost-SAMME and Bagging.