Дифузійна МРТ — Вікіпедія

Дифузійна МРТ (Дифузійно-зважена магнітно-резонансна томографія, або англ. DWI, або DW-MRI) — це метод медичної візуалізації, який дозволяє візуалізувати рух молекул води в біологічних тканинах. Цей метод заснований на вимірюванні дифузії молекул води в тканинах. Найчастіше використовується в нейровізуалізації.

Дифузійна МРТ — це використання певних послідовностей МРТ, в поєднанні з спеціальним програмним забезпеченням, яке генерує зображення з отриманих даних, та використовує дифузію молекул води для генерування контрасту в вихідних МРТ-зображеннях.^[1][2][3] Це дозволяє відображати процес дифузії молекул, головним чином води, у біологічних тканинах in vivo та неінвазивно.

При дифузійному МРТ до тканини прикладається магнітне поле, яке змушує молекули води рухатися в певному напрямку. Швидкість руху вимірюється, і ця інформація використовується для створення зображення тканини. Вимірюючи дифузію молекул води, дифузійна МРТ може надати інформацію про мікроструктуру тканин, включаючи розмір і форму клітин, щільність клітинних мембран і наявність волокон. Таким чином, моделі дифузії молекул води можуть виявити мікроскопічні деталі архітектури тканини, як здорової, так і у патологічному стані.

Дифузійна МРТ широко використовується в неврології для вивчення структури конектому мозку. Дифузійна МРТ також використовується в інших областях медицини, включаючи онкологію, де її можна використовувати для виявлення та моніторингу пухлин, і в кардіології, де її можна використовувати для оцінки пошкодження серцевого м'яза.

Спеціальний вид дифузійної МРТ — дифузійне тензорне зображення (англ. DTI) — широко використовувався для картографії білої речовини мозку.

У дифузійно-зваженому зображенні (DWI) інтенсивність кожного елемента зображення (вокселя) відображає найкращу оцінку швидкості дифузії води в цьому місці. Оскільки рухливість води обумовлена термічним хвилюванням і сильно залежить від її клітинного середовища, гіпотеза DWI полягає в тому, що результати можуть вказувати на (ранні) патологічні зміни. Наприклад, DWI більш чутливий до ранніх змін після інсульту, ніж більш традиційні вимірювання МРТ, такі як швидкість релаксації T1 або T2.

Варіант дифузійно-зваженого зображення, зображення дифузійного спектру (англ. DSI),^[5] було використано для отримання наборів даних Connectome; DSI — це варіант дифузійно-зваженого зображення, який чутливий до внутрішньовоксельних неоднорідностей у напрямках дифузії, спричинених перетином волоконних шляхів, і, таким чином, дозволяє точніше відображати траєкторії аксонів, ніж інші підходи до дифузійного зображення.^[6]

Дифузійно-зважені зображення корисні для діагностики судинних інсультів у мозку. Він також все частіше використовується для визначення стадії недрібноклітинного раку легенів, де він є серйозним кандидатом на заміну позитронно-емісійної томографії як «золотого стандарту» для цього типу захворювання.

Дифузійне тензорне зображення розробляється для вивчення захворювань білої речовини головного мозку, а також для дослідження інших тканин тіла (див. нижче). DWI найчастіше застосовують, коли в досліджуваній тканині переважає ізотропний рух води, наприклад, в сірій речовині в корі головного мозку та головних ядрах головного мозку — в тілі, де швидкість дифузії виглядає однаковою при вимірюванні вздовж будь-якої осі. Однак DWI також залишається чутливим до релаксації T1 і T2. Щоб поєднати ефекти дифузії та релаксації на контрасті зображення, можна отримати кількісні зображення коефіцієнта дифузії, або точніше видимого коефіцієнта дифузії (ADC).

Дифузійна тензорна візуалізація (DTI) досліджує нейронні аксони білої речовини в мозку або м’язові волокна в серці — ті що мають внутрішню волокнисту структуру, аналогічну анізотропії деяких кристалів. В такому середовищі вода буде дифундувати швидше у напрямку, узгодженому з внутрішньою структурою (осьова дифузія), і повільніше, коли вона рухається перпендикулярно бажаному напрямку (радіальна дифузія). Це також означає, що виміряна швидкість дифузії буде відрізнятися залежно від напрямку, з якого дивиться спостерігач.

Зображення базового спектру дифузії (DBSI) додатково розділяє сигнали DTI на дискретні анізотропні тензори дифузії та спектр ізотропних тензорів дифузії, щоб краще диференціювати субвоксельні клітинні структури. Наприклад, тензори анізотропної дифузії корелюють з аксональними волокнами, тоді як тензори низької ізотропної дифузії корелюють з клітинами, а тензори високої ізотропної дифузії корелюють з більшими структурами (такими як шлуночки мозку).^[7]

При дифузійно-зваженій візуалізації (DWI), зазвичай, застосовуються три градієнтні напрямки, достатні для оцінки сліду тензора дифузії або «середньої дифузії», передбачуваного показника набряку. Клінічні зображення виявилися дуже корисними для діагностики судинних інсультів у головному мозку шляхом раннього виявлення (протягом кількох хвилин) гіпоксичного набряку.^[8]

Розширені сканування DTI отримують інформацію про напрямок нервового тракту з даних за допомогою тривимірних або багатовимірних векторних алгоритмів на основі шести або більше напрямків градієнта, достатніх для обчислення тензора дифузії. Модель тензора дифузії є досить простою моделлю процесу дифузії, яка передбачає однорідність і лінійність дифузії в межах кожного вокселя зображення.^[8] За допомогою тензора дифузії можна обчислити показники анізотропії дифузії, такі як фракційна анізотропія (FA). Крім того, основний напрямок тензора дифузії можна використовувати для висновку про зв’язок між білою речовиною мозку (тобто трактографія – спроба побачити, яка частина мозку з’єднана з іншою частиною).

Нещодавно були запропоновані більш досконалі моделі процесу дифузії, спрямовані на подолання недоліків моделі тензора дифузії. Наприклад, зображення в q-просторі ^[9] та узагальнене тензорне зображення дифузії.

Дифузійна візуалізація — це метод медичної візуалізації що базується на МРТ, який створює in vivo магнітно-резонансні зображення біологічних тканин, сенсибілізованих локальними характеристиками молекулярної дифузії, як правило, води (але й інші компоненти також можна досліджувати за допомогою МР-спектроскопічних підходів).^[10]

МРТ можна зробити чутливим до руху молекул. МРТ використовує поведінку протонів у воді для створення контрасту між клінічно значущими характеристиками конкретного суб’єкта. Універсальний характер МРТ пояснюється цією здатністю виробляти контраст, пов’язаний зі структурою тканин на мікроскопічному рівні. У типовому ${\displaystyle T_{1}}$ -зважене зображення, молекули води в зразку збуджуються накладенням сильного магнітного поля. Це змушує багато протонів у молекулах води одночасно прецесувати, виробляючи сигнали на МРТ. в ${\displaystyle T_{2}}$ -зважені зображення, контраст створюється шляхом вимірювання втрати когерентності або синхронності між протонами води. Коли вода знаходиться в середовищі, де вона може вільно перекидатися, релаксація зазвичай займає більше часу. У певних клінічних ситуаціях це може створити контраст між областю патології та навколишньою здоровою тканиною.

Для підвищення чутбливості зображень МРТ до дифузії, напруженість магнітного поля (B1) змінюється лінійно імпульсним градієнтом поля. Оскільки прецесія пропорційна силі магніту, протони починають прецесувати з різною швидкістю, що призводить до дисперсії фази та втрати сигналу. Інший градієнтний імпульс застосовується такої ж величини, але в протилежному напрямку, щоб перефокусувати або змінити фазу обертів. Перефокусування не буде ідеальним для протонів, які рухалися протягом інтервалу часу між імпульсами, і сигнал, виміряний апаратом МРТ, таким чином, знижується. Цей метод «імпульсного градієнта поля» спочатку був розроблений для ЯМР Стейскалом і Таннером^[11], які вивели зменшення сигналу через застосування градієнта імпульсу, пов’язаного з кількістю дифузії, що відбувається, за допомогою такого рівняння:

${\displaystyle {\frac {S(TE)}{S_{0}}}=\exp \left[-\gamma ^{2}G^{2}\delta ^{2}\left(\Delta -{\frac {\delta }{3}}\right)D\right]}$

де ${\displaystyle S_{0}}$ – інтенсивність сигналу без дифузійного зважування, ${\displaystyle S}$ – сигнал з градієнтом, ${\displaystyle \gamma }$ – це гіромагнітне відношення, ${\displaystyle G}$ – сила градієнтного імпульсу, ${\displaystyle \delta }$ – тривалість імпульсу, ${\displaystyle \Delta }$ – це час між двома імпульсами, і, нарешті, ${\displaystyle D}$ – коефіцієнт дифузії.

Щоб локалізувати це ослаблення сигналу, щоб отримати зображення дифузії, необхідно поєднати імпульсні градієнтні імпульси магнітного поля, які використовуються для МРТ (спрямовані на локалізацію сигналу, але ці градієнтні імпульси надто слабкі, щоб створити пов’язане з дифузією ослаблення) з додатковими " вимірювання руху» градієнтні імпульси, згідно з методом Стейскала і Таннера. Ця комбінація не є тривіальною, оскільки перехресні члени виникають між усіма градієнтними імпульсами. Тоді рівняння, встановлене Стейскалом і Таннером, стає неточним, і ослаблення сигналу потрібно обчислювати аналітично або чисельно, інтегруючи всі градієнтні імпульси, присутні в послідовності МРТ, і їх взаємодію. Результат швидко стає дуже складним, враховуючи багато імпульсів, присутніх у послідовності МРТ, і для спрощення Ле Біан запропонував зібрати всі градієнтні члени у «факторі b» (який залежить лише від параметрів отримання), щоб ослаблення сигналу просто стає^[1]:

${\displaystyle {\frac {S(TE)}{S_{0}}}=\exp(-b\cdot ADC)}$

Крім того, коефіцієнт дифузії, ${\displaystyle D}$, замінюється уявним коефіцієнтом дифузії, ${\displaystyle ADC}$, щоб вказати, що процес дифузії не є вільним у тканинах, а перешкоджає та модулюється багатьма механізмами (обмеження в замкнутих просторах, звивистість навколо перешкод тощо), а також інші джерела інтравоксельного некогерентного руху (IVIM), такі як кровотік у невеликих судини або спинномозкова рідина в шлуночках також сприяють ослабленню сигналу. Зрештою, зображення «зважуються» за допомогою процесу дифузії: у цих дифузійно-зважених зображеннях (DWI) сигнал тим більше ослаблений, чим швидша дифузія і чим більший коефіцієнт b. Однак ці дифузійно-зважені зображення все ще також чутливі до контрасту релаксації T1 і T2, що іноді може вводити в оману. Можна розрахувати «чисті» дифузійні карти (або точніше карти ADC, де ADC є єдиним джерелом контрасту), збираючи зображення з принаймні 2 різними значеннями, ${\displaystyle b_{1}}$ і ${\displaystyle b_{2}}$, коефіцієнта b відповідно до:

${\displaystyle \mathrm {ADC} (x,y,z)=\ln[S_{2}(x,y,z)/S_{1}(x,y,z)]/(b_{1}-b_{2})}$

Незважаючи на те, що ця концепція ADC була надзвичайно успішною, особливо для клінічних застосувань, нещодавно вона була оскаржена, оскільки були представлені нові, більш комплексні моделі дифузії в біологічних тканинах. Ці моделі були необхідні, оскільки дифузія в тканинах не є вільною. При такій умові, АЦП, здається, залежить від вибору значень b (здається, що АЦП зменшується при використанні більших значень b), оскільки графік ln(S/So) не є лінійним із коефіцієнтом b, як очікується від рівняння вище. Це відхилення від поведінки вільної дифузії робить дифузійну МРТ такою успішною, оскільки АЦП досить чутливий до змін мікроструктури тканини.

З іншого боку, моделювання дифузії в тканинах стає дуже складним. Серед найбільш популярних моделей є біекспоненціальна модель, яка припускає наявність 2 водних басейнів у повільному або проміжному обміні^[12][13] та модель кумулянтного розширення (також звана ексцесом)^[14][15][16], яка не обов'язково потребує наявності 2 басейнів.

Враховуючи концентрацію ${\displaystyle \rho }$ і потік ${\displaystyle J}$, перший закон Фіка визначає залежність між потоком й градієнтом концентрації:

${\displaystyle J(x,t)=-D\nabla \rho (x,t)}$

де D – коефіцієнт дифузії. Тоді, враховуючи збереження маси, рівняння безперервності пов’язує похідну концентрації за часом з дивергенцією потоку:

${\displaystyle {\frac {\partial \rho (x,t)}{\partial t}}=-\nabla \cdot J(x,t)}$

Зібравши ці два разом, ми отримаємо рівняння дифузії :

${\displaystyle {\frac {\partial \rho (x,t)}{\partial t}}=D\nabla ^{2}\rho (x,t).}$

За відсутності дифузії зміна ядерної намагніченості з часом визначається класичним рівнянням Блоха

${\displaystyle {\frac {d{\vec {M}}}{dt}}=\gamma {\vec {M}}\times {\vec {B}}-{\frac {M_{x}{\vec {i}}+M_{y}{\vec {j}}}{T_{2}}}-{\frac {(M_{z}-M_{0}){\vec {k}}}{T_{1}}}}$

яке має терміни для прецесії, релаксації T2 й релаксації T1.

У 1956 році Г. К. Торрі математично показав, як зміняться рівняння Блоха для намагніченості з додаванням дифузії.^[17] Торрі змінив початковий опис поперечної намагніченості Блоха, включивши в нього терміни дифузії та застосування градієнта, що змінюється в просторі. Оскільки намагніченість ${\displaystyle M}$ є вектором, існує 3 рівняння дифузії, по одному для кожного виміру. Рівняння Блоха-Торрі має вигляд:

${\displaystyle {\frac {d{\vec {M}}}{dt}}=\gamma {\vec {M}}\times {\vec {B}}-{\frac {M_{x}{\vec {i}}+M_{y}{\vec {j}}}{T_{2}}}-{\frac {(M_{z}-M_{0}){\vec {k}}}{T_{1}}}+\nabla \cdot {\vec {D}}\nabla {\vec {M}}}$

де ${\displaystyle {\vec {D}}}$ тепер є тензором дифузії.

Для найпростішого випадку, коли дифузія є ізотропною, тензор дифузії є кратним тотожності:

${\displaystyle {\vec {D}}=D\cdot {\vec {I}}=D\cdot {\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}},}$

тоді рівняння Блоха-Торрі матиме розв’язок

${\displaystyle {M}={M}_{\text{bloch}}e^{-{\frac {1}{3}}\gamma ^{2}G^{2}t^{3}D}\sim e^{-bD_{0}}}$

Експоненціальний член це ${\displaystyle A}$. Анізотропна дифузія матиме подібне рішення для тензора дифузії, окрім того, що буде вимірюватися видимимим коефіцієнтом дифузії (ADC). Загалом ${\displaystyle A}$ таке:

${\displaystyle A=e^{-\sum _{i,j}b_{ij}D_{ij}}}$

де ${\displaystyle b_{ij}}$ терміни включають градієнтні поля ${\displaystyle G_{x}}$, ${\displaystyle G_{y}}$, і ${\displaystyle G_{z}}$ .

Стандартні відтінки сірого для зображень DWI представляють підвищене обмеження дифузії як яскравіше. ^[18]

Зображення з уявним коефіцієнтом дифузії (ADC) або карта ADC — це МРТ-зображення, яке точніше показує дифузію, ніж звичайний DWI, шляхом усунення зважування T2, яке в іншому випадку властиве звичайному DWI. ^[19][20] Зображення АЦП робить це шляхом отримання кількох звичайних зображень DWI з різними значеннями зважування DWI, а зміна сигналу пропорційна швидкості дифузії. На відміну від зображень DWI, стандартні відтінки сірого зображень ADC представляють меншу величину дифузії як темнішу. ^[18]

Церебральний інфаркт призводить до обмеження дифузії, і різниця між зображеннями з різними зважуваннями DWI буде незначною, що призведе до зображення ADC із низьким сигналом у зоні інфаркту. ^[19] Зниження ADC може бути виявлено через кілька хвилин після інфаркту мозку. ^[21] Високий сигнал інфарктної тканини на традиційному DWI є результатом його часткового зважування T2. ^[22]

Дифузійна тензорна томографія (DTI) — це метод магнітно-резонансної томографії, який дає змогу вимірювати обмежену дифузію води в тканині для отримання зображень нервового тракту замість використання цих даних виключно з метою призначення контрасту або кольорів пікселям у хресті. -розріз зображення. Він також надає корисну структурну інформацію про м’язи, включаючи серцевий м’яз, а також інші тканини, такі як простата. ^[23]

У DTI кожен воксель має одну або кілька пар параметрів: швидкість дифузії та бажаний напрямок дифузії — описаний у термінах тривимірного простору — для якого цей параметр дійсний. Властивості кожного вокселя одного зображення DTI зазвичай обчислюються за допомогою векторної або тензорної математики з шести або більше різних дифузійно-зважених отриманих даних, кожне з яких отримано з іншою орієнтацією градієнтів дифузійної сенсибілізації. У деяких методах сотні вимірювань, кожне з яких становить повне зображення, виконуються для створення єдиного кінцевого обчисленого набору даних зображення. Вищий інформаційний вміст вокселя DTI робить його надзвичайно чутливим до тонкої патології в мозку. Крім того, спрямована інформація може бути використана на вищому рівні структури для вибору та відстеження нервових шляхів через мозок — процес, який називається трактографією . ^[24]

Більш точне твердження процесу отримання зображення полягає в тому, що інтенсивність зображення в кожній позиції послаблюється залежно від сили (значення b ) і напрямку так званого градієнта магнітної дифузії, а також від локальної мікроструктури, в якій молекули води дифундують. Чим більше ослаблене зображення в даному положенні, тим більша дифузія в напрямку градієнта дифузії. Щоб виміряти повний профіль дифузії тканини, необхідно повторити МРТ-сканування, застосовуючи різні напрямки (і, можливо, сили) градієнта дифузії для кожного сканування.

Дифузійна МРТ спирається на математичні та фізичні інтерпретації геометричних величин, відомих як тензори . Лише окремий випадок загального математичного поняття має відношення до зображення, яке базується на концепції симетричної матриці . ^{[notes 1]} Дифузія сама по собі є тензоріальною, але в багатьох випадках мета полягає не в спробі вивчити дифузію в мозку як таку, а просто в спробі скористатися перевагами анізотропії дифузії в білій речовині для визначення орієнтації аксонів і величини або ступінь анізотропії. Тензори реально фізично існують у матеріалі чи тканині, тому вони не рухаються, коли система координат, яка використовується для їх опису, обертається. Існує багато різних можливих зображень тензора (рангу 2), але серед них ця дискусія зосереджена на еліпсоїді через його фізичну значущість для дифузії та через його історичне значення в розвитку зображення дифузійної анізотропії в МРТ.

Наступна матриця відображає компоненти тензора дифузії:

${\displaystyle {\bar {D}}={\begin{vmatrix}D_{\color {red}xx}&D_{xy}&D_{xz}\\D_{xy}&D_{\color {red}yy}&D_{yz}\\D_{xz}&D_{yz}&D_{\color {red}zz}\end{vmatrix}}}$

Та сама матриця чисел може мати одночасне друге використання для опису форми та орієнтації еліпса, і ту саму матрицю чисел можна використовувати одночасно в третій спосіб для матричної математики для сортування власних векторів і власних значень, як пояснюється нижче.

Ідея тензора у фізичній науці розвинулась із спроб описати кількість фізичних властивостей. Перші властивості, до яких їх застосували, були властивості, які можна описати одним числом, наприклад температура. Властивості, які можна описати таким чином, називаються скалярами ; їх можна вважати тензорами рангу 0 або тензорами 0-го порядку. Тензори також можна використовувати для опису величин, які мають спрямованість, таких як механічна сила. Ці величини потребують уточнення як величини, так і напрямку, і часто представлені вектором . Тривимірний вектор можна описати трьома компонентами: його проекцією на осі x, y та z . Вектори такого типу можна вважати тензорами рангу 1 або тензорами 1-го порядку.

Тензор часто є фізичною або біофізичною властивістю, яка визначає зв’язок між двома векторами. Коли до об’єкта прикладається сила, може виникнути рух. Якщо рух відбувається в одному напрямку, то перетворення можна описати за допомогою вектора — тензора рангу 1. Однак у тканині дифузія призводить до руху молекул води вздовж траєкторій, які з часом проходять у кількох напрямках, що призводить до складної проекції на декартову вісь. Ця картина є відтворюваною, якщо однакові умови та сили застосовуються до тієї самої тканини однаково. Якщо існує внутрішня анізотропна організація тканини, яка стримує дифузію, то цей факт буде відображено в структурі дифузії. Зв'язок між властивостями рушійної сили, яка створює дифузію молекул води, і результуючою схемою їх руху в тканині можна описати тензором. Сукупність молекулярних зсувів цієї фізичної властивості можна описати за допомогою дев’яти компонентів, кожен з яких пов’язаний з парою осей xx, yy, zz, xy, yx, xz, zx, yz, zy . ^[25] Їх можна записати у вигляді матриці, подібної до тієї, що на початку цього розділу.

Подібним чином відбувається дифузія від точкового джерела в анізотропному середовищі білої речовини. Перший імпульс градієнта дифузії Стейскала Таннера^[26] ефективно позначає деякі молекули води, а другий імпульс ефективно показує їх зміщення внаслідок дифузії. Кожен застосований напрям градієнта вимірює рух уздовж напрямку цього градієнта. Шість або більше градієнтів підсумовуються, щоб отримати всі вимірювання, необхідні для заповнення матриці, припускаючи, що вона симетрична вище та нижче діагоналі (червоні індекси).

У 1848 році Анрі Юро де Сенармон ^[27] застосував нагріту точку до полірованої кристалічної поверхні, яка була покрита воском. У деяких матеріалах, які мали «ізотропну» структуру, кільце розплаву поширювалося по поверхні по колу. В анізотропних кристалах розворот мав форму еліпса. У трьох вимірах цей розкид є еліпсоїдом. Як показав Адольф Фік у 1850-х роках, дифузія демонструє багато тих самих моделей, що й ті, що спостерігаються при передачі тепла.

На цьому етапі корисно розглянути математику еліпсоїдів. Еліпсоїд можна описати формулою: ax ² + на ² + cz ² = 1. Це рівняння описує квадратичну поверхню. Відносні значення a, b і c визначають, чи описує квадрика еліпсоїд чи гіперболоїд .

Як виявилося, можна додати ще три компоненти: сокира ² + на ² + cz ² + диз + ezx + fxy = 1. Багато комбінацій a, b, c, d, e і f все ще описують еліпсоїди, але додаткові компоненти ( d, e, f ) описують обертання еліпсоїда відносно ортогональних осей декартової системи координат. Ці шість змінних можна представити матрицею, подібною до тензорної матриці, визначеної на початку цього розділу (оскільки дифузія є симетричною, то нам потрібно лише шість замість дев’яти компонентів — компоненти під діагональними елементами матриці такі ж, як і компоненти над діагоналлю). Це те, що мається на увазі, коли стверджується, що компоненти матриці тензора другого порядку можна представити еліпсоїдом: якщо значення дифузії шести членів квадратичного еліпсоїда помістити в матрицю, це породить еліпсоїд під кутом поза ортогональною сіткою. Його форма буде більш витягнутою, якщо відносна анізотропія висока.

Коли еліпсоїд/тензор представлено матрицею, ми можемо застосувати корисну техніку зі стандартної матричної математики та лінійної алгебри, тобто « діагоналізувати » матрицю. У зображенні це має два важливі значення. Ідея полягає в тому, що існує два еквівалентні еліпсоїди — однакової форми, але різного розміру та орієнтації. Перший — це виміряний дифузійний еліпсоїд, розташований під кутом, визначеним аксонами, а другий — ідеально вирівняний із трьома декартовими осями. Термін «діагоналізація» відноситься до трьох компонентів матриці вздовж діагоналі від верхнього лівого до нижнього правого кута (компоненти з червоними індексами в матриці на початку цього розділу). Змінні ax ², by ² і cz ² розташовані по діагоналі (червоні нижні індекси), але змінні d, e і f є «поза діагоналлю». Тоді стає можливим виконати крок векторної обробки, на якому ми переписуємо нашу матрицю та замінюємо її новою матрицею, помноженою на три різні вектори одиничної довжини (довжина=1,0). Матриця діагоналізована, оскільки всі недіагональні компоненти тепер дорівнюють нулю. Кути повороту, необхідні для досягнення цієї еквівалентної позиції, тепер з’являються в трьох векторах і можуть бути прочитані як компоненти x, y та z кожного з них. Ці три вектори називаються « власними векторами » або характерними векторами. Вони містять інформацію про орієнтацію вихідного еліпсоїда. Тепер три осі еліпсоїда розташовані прямо вздовж головних ортогональних осей системи координат, тому ми можемо легко визначити їхню довжину. Ці довжини є власними або характерними значеннями.

Діагоналізація матриці виконується шляхом знаходження другої матриці, на яку її можна помножити, з подальшим множенням на обернену другу матрицю, де результатом є нова матриця, у якій три діагональні компоненти ( xx, yy, zz ) мають числа в їх, але недіагональні компоненти ( xy, yz, zx ) дорівнюють 0. Друга матриця надає інформацію про власний вектор .

У сучасній клінічній неврології різні патології мозку можна найкраще виявити, дивлячись на певні показники анізотропії та дифузії. Основний фізичний процес дифузії змушує групу молекул води виходити з центральної точки та поступово досягати поверхні еліпсоїда, якщо середовище анізотропне (це буде поверхня сфери для ізотропного середовища). Формалізм еліпсоїда також функціонує як математичний метод організації тензорних даних. Вимірювання тензора еліпсоїда також дозволяє провести ретроспективний аналіз, щоб зібрати інформацію про процес дифузії в кожному вокселі тканини. ^[28]

В ізотропному середовищі, такому як спинномозкова рідина, молекули води рухаються внаслідок дифузії, і вони рухаються з однаковою швидкістю в усіх напрямках. Знаючи детальні ефекти градієнтів дифузії, ми можемо створити формулу, яка дозволяє нам перетворити ослаблення сигналу вокселя МРТ у числову міру дифузії — коефіцієнт дифузії D . Коли різні бар’єри та обмежувальні фактори, такі як клітинні мембрани та мікротрубочки, заважають вільній дифузії, ми вимірюємо «очевидний коефіцієнт дифузії» або ADC, оскільки вимірювання пропускає всі локальні ефекти та розглядає затухання так, ніби всі швидкості руху були рівними. виключно за рахунок броунівського руху . ADC в анізотропній тканині змінюється залежно від напрямку, в якому він вимірюється. Дифузія відбувається швидко вздовж (паралельно) аксона і повільніше перпендикулярно йому.

Після того, як ми виміряли воксель із шести або більше напрямків і внесли поправки на ослаблення через ефекти T2 і T1, ми можемо використовувати інформацію з нашого розрахованого тензора еліпсоїда, щоб описати, що відбувається у вокселі. Якщо ви розглядаєте еліпсоїд, розташований під кутом у декартовій сітці, тоді ви можете розглянути проекцію цього еліпса на три осі. Три проекції можуть дати вам ADC уздовж кожної з трьох осей ADC _x, ADC _y, ADC _z . Це призводить до ідеї опису середньої дифузії у вокселі, яка буде простою

${\displaystyle (ADC_{x}+ADC_{y}+ADC_{z})/3=ADC_{i}}$

Ми використовуємо індекс i, щоб позначити, що таким буде коефіцієнт ізотропної дифузії з усередненим ефектом анізотропії.

Сам еліпсоїд має головну довгу вісь, а потім ще дві малі осі, які описують його ширину та глибину. Всі три з них перпендикулярні один одному і перетинаються в центральній точці еліпсоїда. Ми називаємо осі в цьому налаштуванні власними векторами, а міри їх довжин — власними значеннями . Довжини позначаються грецькою літерою λ . Довга, спрямована вздовж напрямку аксона, матиме λ ₁, а дві маленькі осі матимуть довжину λ ₂ і λ ₃ . У налаштуваннях тензорного еліпсоїда DTI ми можемо розглядати кожен із них як міру дифузії вздовж кожної з трьох основних осей еліпсоїда. Це трохи відрізняється від АЦП, оскільки це була проекція на вісь, тоді як λ є фактичним вимірюванням еліпсоїда, який ми розрахували.

Коефіцієнт дифузії вздовж головної осі λ ₁ також називається поздовжнім _{коефіцієнтом} дифузії, осьовим коефіцієнтом дифузії або навіть паралельним коефіцієнтом дифузії λ∥ . Історично це найближче до того, що Річардс спочатку виміряв за допомогою векторної довжини в 1991 році ^[29]. Коефіцієнт дифузії на двох малих осях часто усереднюють, щоб отримати міру радіального коефіцієнта дифузії.

${\displaystyle \lambda _{\perp }=(\lambda _{2}+\lambda _{3})/2.}$

Ця величина є оцінкою ступеня обмеження через мембрани та інші ефекти та виявляється чутливим показником дегенеративної патології при деяких неврологічних станах. ^[30] Її також можна назвати перпендикулярною дифузією ( ${\displaystyle \lambda _{\perp }}$ ).

Іншим часто використовуваним показником, який підсумовує загальну дифузію, є Trace — який є сумою трьох власних значень,

${\displaystyle \mathrm {tr} (\Lambda )=\lambda _{1}+\lambda _{2}+\lambda _{3}}$

де ${\displaystyle \Lambda }$ є діагональною матрицею з власними значеннями ${\displaystyle \lambda _{1}}$, ${\displaystyle \lambda _{2}}$ і ${\displaystyle \lambda _{3}}$ по його діагоналі.

Якщо ми розділимо цю суму на три, ми отримаємо середню дифузію ,

${\displaystyle \mathrm {MD} =(\lambda _{1}+\lambda _{2}+\lambda _{3})/3}$

що дорівнює ADC _i , оскільки

${\displaystyle {\begin{aligned}\mathrm {tr} (\Lambda )/3&=\mathrm {tr} (V^{-1}V\Lambda )/3\\&=\mathrm {tr} (V\Lambda V^{-1})/3\\&=\mathrm {tr} (D)/3\\&=ADC_{i}\end{aligned}}}$

де ${\displaystyle V}$ є матрицею власних векторів і ${\displaystyle D}$ – тензор дифузії. Окрім опису рівня дифузії, часто важливо описати відносний ступінь анізотропії у вокселі. На одному полюсі буде сфера ізотропної дифузії, а на іншому полюсі буде дуже тонкий витягнутий сфероїд у формі сигари чи олівця. Найпростіша міра отримується діленням найдовшої осі еліпсоїда на найкоротшу = ( λ ₁ / λ ₃ ). Однак це виявилося дуже сприйнятливим до шуму вимірювання, тому були розроблені дедалі складніші заходи для фіксації вимірювання при мінімізації шуму. Важливим елементом цих розрахунків є сума квадратів різниць коефіцієнтів дифузії = ( λ ₁ − λ ₂ ) ² + ( λ ₁ − λ ₃ ) ² + ( λ ₂ − λ ₃ ) ² . Ми використовуємо квадратний корінь із суми квадратів, щоб отримати щось на кшталт зваженого середнього з домінуванням найбільшого компонента. Одна з цілей полягає в тому, щоб число було близько 0, якщо воксель сферичний, але близько 1, якщо він витягнутий. Це призводить до дробової анізотропії або FA, яка є квадратним коренем із суми квадратів (SRSS) різниць коефіцієнтів дифузії, поділеної на SRSS коефіцієнтів дифузії. Коли друга і третя осі малі відносно головної осі, число в чисельнику майже дорівнює числу в знаменнику. Також множимо на ${\displaystyle 1/{\sqrt {2}}}$ так що FA має максимальне значення 1. Вся формула FA виглядає так:

${\displaystyle \mathrm {FA} ={\frac {\sqrt {3((\lambda _{1}-\operatorname {E} [\lambda ])^{2}+(\lambda _{2}-\operatorname {E} [\lambda ])^{2}+(\lambda _{3}-\operatorname {E} [\lambda ])^{2})}}{\sqrt {2(\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2})}}}}$

Дробову анізотропію також можна розділити на лінійну, плоску та сферичну, залежно від «форми» дифузійного еліпсоїда. ^[31] Наприклад, витягнутий еліпсоїд у формі «сигари» вказує на чітко лінійну анізотропію, «літаюча тарілка» або сплюснутий сфероїд представляє дифузію в площині, а сфера вказує на ізотропну дифузію, рівну в усіх напрямках. ^[32] Якщо власні значення вектора дифузії відсортовані так, що ${\displaystyle \lambda _{1}\geq \lambda _{2}\geq \lambda _{3}\geq 0}$, то заходи можна розрахувати наступним чином:

Для лінійного випадку, де ${\displaystyle \lambda _{1}\gg \lambda _{2}\simeq \lambda _{3}}$ ,

${\displaystyle C_{l}={\frac {\lambda _{1}-\lambda _{2}}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}}$

Для плоского випадку, де ${\displaystyle \lambda _{1}\simeq \lambda _{2}\gg \lambda _{3}}$ ,

${\displaystyle C_{p}={\frac {2(\lambda _{2}-\lambda _{3})}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}}$

Для сферичного випадку, де ${\displaystyle \lambda _{1}\simeq \lambda _{2}\simeq \lambda _{3}}$ ,

${\displaystyle C_{s}={\frac {3\lambda _{3}}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}}$

Кожна міра лежить між 0 і 1, і їх сума дорівнює одиниці. Для опису відхилення від сферичного випадку можна використовувати додаткову міру анізотропії :

${\displaystyle C_{a}=C_{l}+C_{p}=1-C_{s}={\frac {\lambda _{1}+\lambda _{2}-2\lambda _{3}}{\lambda _{1}+\lambda _{2}+\lambda _{3}}}}$

Існують інші показники анізотропії, включаючи відносну анізотропію (RA):

${\displaystyle \mathrm {RA} ={\frac {\sqrt {(\lambda _{1}-\operatorname {E} [\lambda ])^{2}+(\lambda _{2}-\operatorname {E} [\lambda ])^{2}+(\lambda _{3}-\operatorname {E} [\lambda ])^{2}}}{{\sqrt {3}}\operatorname {E} [\lambda ]}}}$

і об'ємний коефіцієнт (VR):

${\displaystyle \mathrm {VR} ={\frac {\lambda _{1}\lambda _{2}\lambda _{3}}{\operatorname {E} [\lambda ]^{3}}}}$

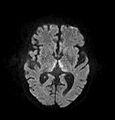
Найбільш поширеним застосуванням традиційного DWI (без DTI) є гостра ішемія головного мозку. DWI безпосередньо візуалізує ішемічний некроз при інфаркті мозку у формі цитотоксичного набряку ^[33], що проявляється як високий сигнал DWI протягом декількох хвилин після закупорки артерії. ^[34] Завдяки перфузійній МРТ, що виявляє як серцевину інфаркту, так і врятовану півтінь, останню можна кількісно визначити за допомогою DWI та перфузійної МРТ. ^[35]

• 
  DWI показує некроз (показується яскравішим)
• 
  DWI показує обмежену дифузію в медіальному дорсальному таламі, що відповідає енцефалопатії Верніке
• 
  DWI показує високий сигнал кортикальної стрічки, що відповідає обмеженню дифузії у пацієнта з відомим синдромом MELAS

Ще одна область застосування DWI - онкологія . Пухлини у багатьох випадках є висококлітинними, що дають обмежену дифузію води, і тому з’являються з відносно високою інтенсивністю сигналу в DWI. ^[36] DWI зазвичай використовується для виявлення та визначення стадії пухлин, а також для моніторингу реакції пухлини на лікування з часом. DWI також можна зібрати для візуалізації всього тіла за допомогою техніки, яка називається «дифузійно-зважене зображення всього тіла з придушенням фонового сигналу тіла» (DWIBS). ^[37] Також було показано, що деякі більш спеціалізовані методи дифузійної МРТ, такі як візуалізація дифузійного ексцесу (DKI), передбачають реакцію хворих на рак на хіміотерапію. ^[38]

Основне застосування – візуалізація білої речовини, де можна виміряти розташування, орієнтацію та анізотропію трактів. Архітектура аксонів у паралельних пучках та їхні мієлінові оболонки сприяють дифузії молекул води переважно вздовж їх основного напрямку. Така переважно орієнтована дифузія називається анізотропною дифузією.

Зображення цієї властивості є розширенням дифузійної МРТ. Якщо застосовано серію дифузійних градієнтів (тобто змін магнітного поля в магніті МРТ), які можуть визначити принаймні 3 вектори спрямованості (використання 6 різних градієнтів є мінімумом, а додаткові градієнти підвищують точність «недіагональної» інформації), можна обчислити для кожного вокселя тензор (тобто симетричну позитивно визначену матрицю 3 × 3), який описує тривимірну форму дифузії. Напрямок волокна вказується головним власним вектором тензора. Цей вектор можна позначити кольором, що дасть картографію положення та напрямку трактів (червоний для лівого-правого, синій для верхнього-нижнього та зелений для переднього-заднього). ^[39] Яскравість зважується дробовою анізотропією, яка є скалярною мірою ступеня анізотропії в даному вокселі. Середня дифузія (MD) або слід — це скалярна міра загальної дифузії в межах вокселя. Ці заходи зазвичай використовуються клінічно для локалізації уражень білої речовини, які не виявляються на інших формах клінічної МРТ. ^[40]

Застосування в мозку:

• Специфічна локалізація уражень білої речовини, таких як травма, і визначення тяжкості дифузної черепно-мозкової травми . Локалізація пухлин по відношенню до трактів білої речовини (інфільтрація, дефлексія) була одним із найважливіших початкових застосувань. При плануванні хірургічного втручання при деяких типах пухлин головного мозку хірургічне втручання допомагає знати близькість і відносне розташування кортикоспинального тракту та пухлини.
• Дані зображення дифузійного тензора можна використовувати для виконання трактографії білої речовини. Алгоритми відстеження волокна можна використовувати для відстеження волокна по всій його довжині (наприклад, кортикоспинального тракту, через який рухова інформація переходить від рухової кори до спинного мозку та периферичних нервів ). Трактографія є корисним інструментом для вимірювання дефіциту білої речовини, наприклад, при старінні. Його оцінка орієнтації та міцності волокон стає дедалі точнішою, і це має широке потенційне значення в галузях когнітивної нейронауки та нейробіології.
• Використання DTI для оцінки білої речовини при розвитку, патології та дегенерації було в центрі уваги понад 2500 наукових публікацій з 2005 року. Це обіцяє бути дуже корисним у відрізненні хвороби Альцгеймера від інших типів деменції . Застосування в дослідженні мозку включає дослідження нейронних мереж in vivo, а також у коннектоміці .

Застосування для периферичних нервів:

• Плечове сплетення : DTI може диференціювати нормальні нерви ^[41] (як показано на трактограмі спинного мозку та плечового сплетення та 3D-реконструкції 4k тут ) від травматично ушкоджених нервових корінців ^[4].
• Синдром кубітального тунелю : показники, отримані з DTI (FA та RD), можуть відрізнити безсимптомних дорослих від тих, у кого компресія ліктьового нерва в ліктьовому суглобі ^[42].
• Синдром зап’ястного каналу : показники, отримані з DTI (нижня FA та MD), відрізняють здорових дорослих від тих, хто має синдром зап’ястного каналу ^[43].

На початку розробки трактографії на основі DTI ряд дослідників вказали на недолік у моделі тензора дифузії. Тензорний аналіз припускає, що в кожному вокселі зображення є один еліпсоїд — ніби всі аксони, що проходять через воксель, рухаються в одному напрямку. ^[44] Це часто правда, але можна підрахувати, що в більш ніж 30% вокселів на зображенні мозку зі стандартною роздільною здатністю є принаймні два різних нейронних тракту, що рухаються в різних напрямках і проходять один через одного. У класичній тензорній моделі дифузійного еліпсоїда інформація з перетину просто виглядає як шум або незрозуміла зменшена анізотропія в заданому вокселі. Девід Тач був одним з перших, хто описав вирішення цієї проблеми. ^{[45] [46]} Ідею найкраще зрозуміти, концептуально розмістивши своєрідний геодезичний купол навколо кожного вокселя зображення. Цей ікосаедр забезпечує математичну основу для проходження через воксель великої кількості рівномірно розташованих градієнтних траєкторій — кожна з яких збігається з однією з вершин ікосаедра. По суті, зараз ми збираємося поглянути на воксель з великої кількості різних напрямків (зазвичай 40 або більше). Ми використовуємо мозаїку " n -tuple", щоб додати більше рівномірно розташованих вершин до оригінального ікосаедра (20 граней) — ідея, яка також мала свої прецеденти в дослідженнях палеомагнетизму кількома десятиліттями раніше. ^[47] Ми просто хочемо знати, які напрямні лінії показують максимальну анізотропну дифузію. Якщо є один тракт, буде лише два максимуми, спрямовані в протилежні сторони. Якщо два тракти перетинаються у вокселі, буде дві пари максимумів і так далі. Ми все ще можемо використовувати тензорну математику, щоб використовувати максимуми для вибору груп градієнтів для упаковки в кілька різних тензорних еліпсоїдів в одному вокселі, або використовувати більш складний аналіз тензорів вищого рангу, ^[48] або ми можемо зробити справді «безмодельний» аналіз який просто вибирає максимуми та продовжує займатися трактографією.

Метод трактографії Q-Ball — це реалізація, у якій Девід Тач пропонує математичну альтернативу тензорній моделі. ^[44] Замість того, щоб примусово вводити дані анізотропії дифузії в групу тензорів, використана математика розгортає як розподіли ймовірностей, так і класичну частину геометричної томографії та векторної математики, розроблену майже 100 років тому — перетворення Фанка Радона. ^[49]

Для DTI, як правило, можна використовувати лінійну алгебру, матричну математику та векторну математику для обробки аналізу тензорних даних.

У деяких випадках цікавить повний набір властивостей тензора, але для трактографії зазвичай необхідно знати лише величину та орієнтацію основної осі чи вектора. Ця головна вісь — та, що має найбільшу довжину — є найбільшим власним значенням, і її орієнтація закодована у її узгодженому власному векторі. Потрібна лише одна вісь, оскільки передбачається, що найбільше власне значення вирівняно з напрямком головного аксона для виконання трактографії.

• Трактографія
• Нейровізуалізація
• Коннектом
• Коннектограма
• Фракційна анізотропія
• Медична візуалізація

• Johansen-Berg, Heidi; Behrens, Timothy E. J. (2014). Diffusion MRI: from quantitative measurement to in vivo neuroanatomy (вид. Second edition). Amsterdam. ISBN 9780123964601
• Jones, Derek K. (2011). Diffusion MRI : theory, methods, and applications. New York: Oxford University Press. ISBN 978-0-19-970870-3.

• Український радіологічний та онкологічний журнал^{[відсутнє в джерелі]}
• Magnetic Resonance in Medicine^{[відсутнє в джерелі]}
• Journal of Magnetic Resonance Imaging^{[відсутнє в джерелі]}
• Magnetic Resonance Imaging^{[відсутнє в джерелі]}
• Magnetic Resonance Materials in Physics, Biology, and Medicine^{[відсутнє в джерелі]}
• Topics in Magnetic Resonance Imaging
• Investigative Radiology^{[відсутнє в джерелі]}
• Medical Image Analysis^{[відсутнє в джерелі]}
• Computerized Medical Imaging and Graphics^{[відсутнє в джерелі]}
• Radiology^{[відсутнє в джерелі]}
• Radiology: Artificial Intelligence^{[відсутнє в джерелі]}