Перетворення Гафа — Вікіпедія
| Перетворення Гафа | |
| Формула | |
|---|---|
| Підтримується Вікіпроєктом | Вікіпедія:Проєкт:Математика |
| | |
| Виявляння ознак |
|---|
| Виявляння контурів |
| Виявляння кутів |
| Виявляння плям |
| Виявляння хребтів |
| Перетворення Гафа |
| Структурний тензор |
| Афінноінваріантне виявляння ознак |
| Опис ознак |
| Простір масштабів |
Перетво́рення Га́фа (англ. Hough transform) — це методика виділяння ознак, вживана в аналізі зображень[en], комп'ютерному баченні та цифровій обробці зображень.[1] Призначення цієї методики — знаходити недосконалі примірники об'єктів певного класу фігур за допомогою процедури голосування. Цю процедуру голосування виконують у просторі параметрів[en], з якого кандидатури об'єктів отримують як локальні максимуми у так званому накопичувальному просторі (англ. accumulator space), явно створюваному алгоритмом для обчислення перетворення Гафа.
Класичне перетворення Гафа стосувалося встановлюванням прямих на зображенні, але пізніше його було розширено для встановлювання положень довільних фігур, найчастіше — кіл або еліпсів. Перетворення Гафа, яке сьогодні використовують повсюдно, було винайдено 1972 року Річардом Дудою[en] та Пітером Гартом[en], які назвали його «узагальненим перетворенням Гафа» (англ. "generalized Hough transform")[2] на честь відповідного патенту Пола Гафа 1962 року.[3][4] Це перетворення було популяризовано у спільноті комп'ютерного бачення Даною Г. Баллард[en] через статтю в журналі 1981 року під назвою «Узагальнення перетворення Гафа для виявляння довільних фігур».
Первинно його було винайдено для машинного аналізу фотографій бульбашкових камер (Гаф, 1959).
Перетворення Гафа було запатентовано 1962 року як U.S. Patent 3 069 654 та передано Комісії з атомної енергії США під назвою «Метод і засоби для розпізнавання складних моделей». У цьому патенті використано параметрування нахилу-відтину для прямих, що незграбно призводить до необмеженого простору перетворення, оскільки нахил може сягати нескінченності.
Параметрування ро-тета, повсюдно використовуване сьогодні, було вперше описано в
- Duda, R.O.; Hart, P. E. (January 1972). Use of the Hough Transformation to Detect Lines and Curves in Pictures. Comm. ACM. 15: 11—15. doi:10.1145/361237.361242. S2CID 1105637. (англ.)
хоча воно вже було стандартом для перетворення Радона щонайменше з 1930-х років.
Варіацію О'Ґормана та Клоуза описано в
- O'Gorman, Frank; Clowes, MB (1976). Finding Picture Edges Through Collinearity of Feature Points. IEEE Trans. Comput. 25 (4): 449—456. doi:10.1109/TC.1976.1674627. S2CID 10851078. (англ.)
Розповідь про те, як було винайдено сучасний вигляд перетворення Гафа, наведено в
- Hart, P. E. (November 2009). How the Hough Transform was Invented (PDF). IEEE Signal Processing Magazine. 26 (6): 18—22. doi:10.1109/msp.2009.934181. S2CID 16245096. Архів оригіналу (PDF) за 16 травня 2018. (англ.)
В автоматизованому аналізі цифрових зображень часто виникає підзадача виявляння простих фігур, таких як прямі, кола або еліпси. У багатьох випадках як етап попередньої обробки можливо використовувати виявляч контурів, щоб отримувати точки або пікселі зображення, які знаходяться на потрібній кривій у просторі зображення. Проте через недосконалість даних зображення або виявляча контурів можуть бути відсутні точки або пікселі на бажаних кривих, а також просторові відхилення між ідеальною прямою/колом/еліпсом і шумними контурними точками, отриманими з виявляча контурів. З цих причин групувати виділені контурні ознаки у відповідний набір прямих, кіл або еліпсів часто нетривіально. Мета перетворення Гафа полягає у розв'язанні цієї проблеми, уможливлюючи групування контурних точок в об'єкти-кандидати шляхом виконання процедури явного голосування над набором параметрованих об'єктів зображення (Шапіро та Стокман, 304).
Найпростіший випадок перетворення Гафа — виявляння прямих. У загальному випадку пряму y = mx + b можливо подати у вигляді точки (b, m) у просторі параметрів. Проте вертикальні прямі становлять проблему. Вони призводили б до необмежених значень параметра нахилу m. Таким чином, з обчислювальних міркувань Дуда й Гарт[5] запропонували використовувати нормальну форму Гессе[en]
де — відстань від початку координат до найближчої точки на прямій, а — кут між віссю та прямою, що сполучає початок координат із цією найближчою точкою.
Інтуїтивне розуміння для цього вигляду, подібно до рівняння площини, полягає в тому, що кожен вектор на прямій мусить бути перпендикулярним (ортогональним) цьому відрізкові довжини що йде від початку координат. Легко побачити, що точка перетину лінії цієї функції та цього перпендикуляра, який виходить з початку координат, перебуває в . Отже, для будь-якої точки на цій прямій вектор мусить бути ортогональним до вектора . Тож ми отримуємо, що для будь-якої точки на лінії цієї функції повинно виконуватися рівняння . Отже, . Оскільки , а , ми отримуємо . Оскільки , ми отримуємо остаточний вигляд .
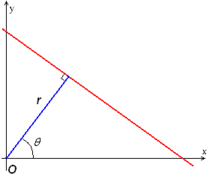
Відтак, із кожною прямою зображення можливо пов'язати пару . Площину іноді називають простором Гафа (англ. Hough space) для множини прямих у двох вимірах. Це подання робить перетворення Гафа концептуально дуже близьким до двовимірного перетворення Радона. Насправді перетворення Гафа математично еквівалентне перетворенню Радона, але обидва перетворення мають різні обчислювальні інтерпретації, традиційно пов'язувані з ними.[6]
Для заданої однієї точки на площині множина всіх прямих, що проходять через неї, відповідає синусоїдній кривій на площині (r, θ), унікальній для цієї точки. Множина з двох або більше точок, які утворюють пряму, даватиме перетин синусоїд на (r, θ) для цієї прямої. Таким чином, задачу виявляння колінеарних точок[en] можливо перетворити на задачу знаходження конкурентних кривих.[7]
Для заданої фігури, параметрованої набором , що набуває значень у множині , званій простором цієї фігури (англ. shape space), перетворення Гафа можливо інтерпретувати як зворотне перетворення розподілу ймовірності в просторі зображення до простору фігури , й інтерпретувати виявляння фігури як оцінювання максимальної правдоподібності.
У явному вигляді, перетворення Гафа виконує наближене наївне баєсове висновування. Ми починаємо з рівномірного апріорного в просторі фігури. Ми розглядаємо лише позитивні свідчення та ігноруємо всі негативні, щоби могти виявляти частково затулені фігури.
Ми підсумовуємо логарифмічну правдоподібність у просторі фігури з точністю до адитивної сталої. Наївне баєсове припущення означає, що всі пікселі в просторі зображення надають незалежні свідчення, тож їхні правдоподібності перемножуються, тобто їхні логарифмічні правдоподібності додаються. Свобода в адитивній сталій дозволяє нам не виконувати жодних операцій над «пікселями тла» в просторі фігури.
Зрештою, ми виконуємо оцінку максимальної правдоподібності, обираючи піки логарифмічної правдоподібності в просторі фігури.[8]
Алгоритм перетворення Гафа для прямих оцінює два параметри, що визначають пряму. Простір перетворення має два виміри, й кожну точку в просторі перетворення використовують як накопичувач для виявляння або встановлювання прямої, описаної рівнянням . Кожна точка на виявлених у зображенні контурах вносить свій внесок у накопичувачі.
Розмірність накопичувача дорівнює числу невідомих параметрів, тобто двом, розглядаючи квантовані значення r та θ в парі (r, θ). Для кожного пікселя в (x, y) та його околу алгоритм перетворення Гафа визначає, чи є достатньо свідчення прямої в цьому пікселі. Якщо так, він розраховує параметри (r, θ) цієї прямої, а потім знаходить засік накопичувача, до якого потрапляють ці параметри, й збільшує значення цього засіку.
Шляхом знаходження засіків із найвищими значеннями, як правило, шляхом пошуку локальних максимумів у накопичувальному просторі, можливо виділяти найправдоподібніші прямі та зчитувати їхні (наближені) геометричні визначення (Шапіро та Стокман, 304). Найпростіший спосіб знаходити ці піки — застосовувати поріг якогось вигляду, але інші методики можуть видавати кращі результати за різних обставин — визначати, які прямі знайдено, а також скільки. Оскільки видані прямі не містять жодної інформації про довжину, на наступному кроці часто необхідно знайти, які частини зображення збігаються з якими прямими. Крім того, через похибки недосконалості на етапі виявляння контурів зазвичай будуть похибки в накопичувальному просторі, що може робити пошук відповідних піків і, отже, відповідних прямих, нетривіальним.
Кінцевий результат перетворення Гафа для прямих — двовимірний масив (матриця), подібна до накопичувача, — одним виміром цієї матриці є квантований кут θ, а іншим — квантована відстань r. Кожен елемент цієї матриці має значення, що дорівнює сумі точок або пікселів, розташованих на прямій, поданій квантованими параметрами (r, θ). Отже, елемент із найвищим значенням вказує пряму, яка найбільше подана у вхідному зображенні.[9]
Розгляньмо три точки даних, показані тут як чорні крапки.

- Через кожну точку даних відкладено декілька прямих, які проходять під різними кутами. Їх тут показано різними кольорами.
- Перетворення Гафа накопичує внески від усіх пікселів у виявленому контурі. Для кожної прямої існує опорний відрізок, який перпендикулярний до неї й перетинає початок координат. У кожному випадку однин з них показано стрілкою.
- Розраховують довжину (тобто перпендикулярну відстань до початку координат) і кут кожного опорного відрізка. Довжини та кути наведено в таблиці під діаграмами.
З цих розрахунків видно, що в усіх випадках опорний відрізок під кутом 60° має схожу довжину. Отже, зрозуміло, що відповідні прямі (сині на зображенні вище) дуже схожі. Таким чином, можливо вважати, що всі точки лежать близько до синьої прямої.
Нижче наведено інший приклад, який показує результати перетворення Гафа на растровому зображенні, що містить дві товсті прямі.
Результати цього перетворення було збережено в матриці. Значення комірок подає кількість кривих через кожну точку. Вищі значення комірок відображено яскравіше. Дві виразно яскраві плями — параметри Гафа цих двох прямих. За положенням цих плям можливо визначити кут і відстань від центру зображення цих двох прямих у первинному зображенні.
Вдосконалення, запропоноване О'Ґорманом і Клоузом, можливо використовувати для виявляння ліній, якщо брати до уваги, що локальний градієнт яскравості зображення обов'язково буде ортогональним до контуру. Оскільки виявляння контурів зазвичай передбачає обчислення величини градієнта яскравості, напрямок градієнта часто знаходять як побічний ефект. Якщо задана точка з координатами (x, y) і справді перебуває на прямій, то локальний напрямок градієнта дає параметр θ, що відповідає згаданій лінії, й тоді негайно отримується параметр r. (Шапіро та Стокман, 305) Напрямок градієнта можливо оцінювати з точністю до 20°, що скорочує синусоїду від повних 180° до приблизно 45°. Це зменшує час обчислення та має цікавий ефект зменшення кількості марних голосів, відтак покращуючи видимість піків, що відповідають реальним прямим на зображенні.
Фернандес та Олівейра[10] запропонували вдосконалену схему голосування для перетворення Гафа, яка дозволяє програмному втіленню досягати продуктивності реального часу навіть на відносно великих зображеннях (напр., 1280×960). Ядрове перетворення Гафа (англ. Kernel-based Hough transform, KHT) використовує те саме параметрування , запропоноване Дудою й Гартом, але працює з кластерами приблизно колінеарних пікселів. Голосування для кожного кластера проводять з використанням спрямованого еліптично-гауссового ядра, яке моделює невизначеність, пов'язану з найкращим допасовуванням прямої до відповідного кластера. Цей підхід не лише значно покращує продуктивність цієї схеми голосування, але також створює набагато чистіший накопичувач і робить перетворення стійкішим до виявляння помилкових ліній.
Лімбергер та Олівейра[11] запропонували детерміновану методику для виявляння площин у невпорядкованих хмарах точок, витратність якої становить відносно кількості зразків, досягаючи продуктивності реального часу для відносно великих наборів даних (до точок на ЦП 3.4 ГГц). Вона ґрунтується на швидкій стратегії голосування перетворення Гафа для планарних областей, натхненна ядровим перетворенням Гафа. Це тривимірне ядрове перетворення Гафа (англ. 3D kernel-based Hough transform, 3DKHT) використовує швидкий і надійний алгоритм сегментування кластерів приблизно копланарних зразків, і віддає голоси за окремі кластери (замість окремих зразків) на сферичному накопичувачі () з використанням тривимірного гауссового ядра. Цей підхід на кілька порядків швидший за наявні (недетерміновані) методики виявляння площин у хмарах точок, такі як рандомізоване перетворення Гафа та RANSAC, і краще масштабується з розміром наборів даних. Його можливо використовувати з будь-яким застосунком, що потребує швидкого виявляння пласких об'єктів на великих наборах даних.
Перетворення Гафа для кривих, і його узагальнення для аналітичних і неаналітичних фігур
[ред. | ред. код]Хоча описана вище версія перетворення стосується лише пошуку прямих, подібне перетворення можливо використовувати для пошуку будь-якої фігури, яку може бути подано набором параметрів. Коло, наприклад, можливо перетворити на набір із трьох параметрів, що подають його центр та радіус, що робить простір Гафа тривимірним. Таким чином також можливо знаходити довільні еліпси та криві, як і будь-яку фігуру, яку легко виразити як набір параметрів.
Фернандес та Олівейра запропонували узагальнення перетворення Гафа для виявляння аналітичних фігур у просторах будь-якої вимірності.[12] На відміну від інших підходів на основі перетворення Гафа для аналітичних фігур, методика Фернандеса не залежить ані від фігури, яку потрібно виявляти, ані від типу вхідних даних. Виявляння може бути доведено до типу аналітичної фігури зміною передбачуваної моделі геометрії, у якій було кодовано дані (наприклад, евклідів простір, проєктивний простір, конформна геометрія тощо), тоді як запропоноване формулювання лишається незмінним. Це також гарантує, що передбачувані фігури подано з найменшою можливою кількістю параметрів, й уможливлює одночасне виявляння різних типів фігур, що найкраще відповідають вхідному набору записів з різними вимірностями та різними геометричними визначеннями (наприклад, одночасне виявляння площин і сфер, які найкраще відповідають набору точок, прямих та кіл).
Для складніших фігур на площині (тобто таких, які неможливо подати аналітично в якомусь двовимірному просторі), використовують узагальнене перетворення Гафа,[13] яке дозволяє ознаці голосувати за певне положення, спрямування та/або масштабування фігури за допомогою попередньо визначеної таблиці пошуку. Це перетворення Гафа накопичує внески від усіх пікселів виявленого контуру.
Детальніші відомості з цієї теми ви можете знайти в статті Перетворення Гафа для кіл[en].
Змінити цей алгоритм для виявляння колових фігур замість прямих ліній відносно просто.
- Спершу ми створюємо накопичувальний простір, який складається з комірки для кожного пікселя. Спочатку кожна комірка має значення 0.
- Для кожної контурної точки (i, j) на зображенні збільшити всі комірки, які відповідно до рівняння кола можуть бути центрами кола. Ці комірки подаються у рівнянні літерою .
- Для кожного можливого значення , знайденого на попередньому кроці, знайти всі можливі значення , що задовольняють рівняння.
- Знайти локальні максимуми у накопичувальному просторі. Ці комірки подають кола, які було виявлено алгоритмом.
Якщо ми не знаємо заздалегідь радіус кола, яке ми намагаємося знайти, ми можемо використовувати тривимірний накопичувальний простір для пошуку кіл довільного радіусу. Природно, це витратніше з погляду обчислень.
Цей метод також може виявляти кола, які частково знаходяться за межами накопичувального простору, якщо в ньому залишається достатня частина кола.
Перетворення Гафа також можливо використовувати для виявляння тривимірних об'єктів у дальнісних даних та тривимірних хмарах точок. Розширення класичного перетворення Гафа для виявляння площин доволі просте. Площину подають її явним рівнянням , для якого ми можемо використовувати тривимірний простір Гафа, що відповідає , та . Це розширення страждає від тих же проблем, що й його двовимірний аналог, тобто, приблизно горизонтальні площини можливо виявляти надійно, тоді як продуктивність падає, коли напрямок площини стає вертикальним (великі значення та посилюють шум у даних). Цю формулу площини використовували для виявляння площин у хмарах точок, отриманих лазерним скануванням з повітря[14], вона працює дуже добре, оскільки в цій області всі площини майже горизонтальні.
Для узагальненого виявляння площин перетворенням Гафа площину можливо параметрувати вектором нормалі (з використанням сферичних координат) та її віддалі від початку координат , в результаті чого утворюється тривимірний простір Гафа. Це призводить до того, що кожна точка вхідних даних голосує за синусоїдну поверхню в просторі Гафа. Перетин цих синусоїдних поверхонь вказує на наявність площини.[15] Загальніший підхід для понад 3 вимірів вимагає, щоб евристика пошуку лишалася здійсненною.[16]
Перетворення Гафа також використовували для пошуку циліндричних об'єктів у хмарах точок за допомогою двоетапного підходу. Перший крок визначає спрямування циліндра, а другий знаходить положення та радіус.[17]
Одна з поширених деталей варіацій: пошук засіків із найбільшою кількістю на одному етапі можливо використовувати для обмеження діапазону значень, шуканих на наступному.
Простір параметрів високої вимірності для перетворення Гафа не лише повільний, але й, при втіленні без попереднього обдумування, може легко переповнювати доступну пам'ять. Навіть якщо середовище програмування дозволяє виділяння масивів, більших за доступний простір пам'яті, через віртуальну пам'ять, то необхідна для цього кількість змін сторінок буде дуже вимогливою, оскільки накопичувальний масив використовується в режимі довільного доступу, нечасто затримуючись на безперервній пам'яті при переходах від індексу до індексу.
Розгляньмо задачу пошуку еліпсів на зображенні 800×600. Якщо припустити, що радіуси еліпсів спрямовано вздовж головних осей, то простір параметрів чотиривимірний. (x, y) визначають центр еліпса, а a та b позначують два радіуси. Дозвіл центрові бути будь-де в зображенні додає обмеження 0<x<800 та 0<y<600. Якщо радіусам надати як обмеження ті самі значення, то залишиться розріджено заповнений накопичувальний масив із понад 230 мільярдами значень.
Навряд чи програмі, задуманій таким чином, буде дозволено виділити достатню кількість пам'яті. Це означає не неможливість розв'язання цієї задачі, а лише необхідність знайти нові способи обмеження розміру накопичувального масиву, що зробить це здійсненним. Наприклад:
- Якщо розумно припустити, що кожен з еліпсів повністю міститься в зображенні, діапазон радіусів можливо зменшити. Радіуси можуть бути найбільшими, якщо центр еліпса перебуває в центрі зображення, що дозволяє контуру еліпса розтягуватися до країв. У цьому крайньому випадку кожен з радіусів може становити лише половину величини розміру зображення того ж напрямку. Зменшення діапазону a та b таким чином зменшує накопичувальний масив до 57 мільярдів значень.
- Точність торгу для простору в оцінюванні центру: якщо центр передбачувати з відхиленням на 3 як по осі x, так і по осі y, це зменшує розмір накопичувального масиву приблизно до 6 мільярдів значень.
- Точність торгу для простору в оцінюванні радіусів: якщо радіуси оцінювати так, щоби кожен був відхилений на 5, відбувається подальше зменшення розміру накопичувального масиву приблизно на 256 мільйонів значень.
- Обрізування зображення до цікавих областей. Це залежить від зображення, а отже, воно непередбачуване, але уявіть випадок, коли всі цікаві контури в зображення знаходяться у верхньому лівому квадранті цього зображення. У цьому випадку накопичувальний масив можливо зменшити ще далі, обмеживши всі 4 параметри коефіцієнтом 2, що дасть загальний коефіцієнт зменшення 16.
При застосуванні до наведеного прикладу лише перших трьох із цих обмежень розмір накопичувального масиву зменшується майже в 1000 разів, доходячи до розміру, який з більшою ймовірністю вміститься в пам'яті сучасного комп'ютера.
Йонхон Сє та Цян Цзі пропонують ефективний спосіб втілення перетворення Гафа для виявлення еліпсів шляхом подолання проблем із пам'яттю.[18] Як зазначено в алгоритмі (на сторінці 2 статті), щоби виявляти еліпси на зображенні, цей підхід використовує лише одновимірний накопичувач (для малої осі). Складність становить O(N3) відносно кількості ненульових точок на зображенні.
Перетворення Гафа є дієвим, лише якщо велика кількість голосів потрапляє до правильного засіку, так що цей засік можливо легко виявити серед шуму тла. Це означає, що засік мусить не бути занадто малим, бо інакше частина голосів потраплятиме до сусідніх засіків, зменшуючи таким чином видимість основного засіку.[19]
Крім того, коли число параметрів велике (тобто, коли ми використовуємо перетворення Гафа із зазвичай понад трьома параметрами), середня кількість голосів, відданих одному засікові, дуже низька, й ті засіки, що відповідають реальній фігурі на зображенні, не обов'язково матимуть набагато більше число голосів, аніж їхні сусіди. Складність зростає зі швидкістю з кожним додатковим параметром, де — розмір простору зображення, а — число параметрів. (Шапіро та Стокман, 310) Тож перетворення Гафа слід використовувати дуже обережно, щоби виявляти щось крім прямих або кіл.
Нарешті, більша частина ефективності перетворення Гафа залежить від якості вхідних даних: щоби перетворення Гафа було ефективним, контури повинно бути виявлено добре. Використання перетворення Гафа на зашумлених зображеннях є дуже делікатною справою, і, як правило, перед ним необхідно використовувати етап знешумлювання. У випадку, коли зображення спотворено поцяткованістю, як у випадку з радіолокаційними зображеннями, перетворення Радона іноді є кращим для виявлення прямих, оскільки воно послаблює шум шляхом підсумовування.
- Узагальнене перетворення Гафа
- Рандомізоване перетворення Гафа
- Перетворення Радона
- Перетворення Фур'є
- ↑ Shapiro, Linda[en] and Stockman, George. "Computer Vision", Prentice-Hall, Inc. 2001 (англ.)
- ↑ Duda, R. O. and P. E. Hart, "Use of the Hough Transformation to Detect Lines and Curves in Pictures," Comm. ACM, Vol. 15, pp. 11–15 (January, 1972) (англ.)
- ↑ Hough, P.V.C. Method and means for recognizing complex patterns, U.S. Patent 3,069,654, Dec. 18, 1962 (англ.)
- ↑ P.V.C. Hough, Machine Analysis of Bubble Chamber Pictures, Proc. Int. Conf. High Energy Accelerators and Instrumentation, 1959 (англ.)
- ↑ Richard O. Duda[en] and Peter E. Hart[en] (April 1971). Use of the Hough Transformation to Detect Lines and Curves in Pictures (PDF). Artificial Intelligence Center[en]. (англ.)
- ↑ A short introduction to the Radon and Hough transforms and how they relate to each other. CiteSeerX. (англ.)
- ↑ Hough Transform. (англ.)
- ↑ Stephens, R. S. (1990). A probabilistic approach to the Hough Transform. Procedings of the British Machine Vision Conference 1990. British Machine Vision Association: 12.1—12.6. doi:10.5244/c.4.12. (англ.)
- ↑ Jensen, Jeppe. Hough Transform for Straight Lines (PDF). Архів оригіналу (PDF) за 26 квітня 2012. Процитовано 16 грудня 2011. (англ.)
- ↑ Fernandes, L.A.F.; Oliveira, M.M. (2008). Real-time line detection through an improved Hough transform voting scheme. Pattern Recognition. 41 (1): 299—314. Bibcode:2008PatRe..41..299F. doi:10.1016/j.patcog.2007.04.003. (англ.)
- ↑ Limberger, F. A.; Oliveira, M. M. (2015). Real-Time Detection of Planar Regions in Unorganized Point Clouds (PDF). Pattern Recognition. 48 (6): 2043—2053. Bibcode:2015PatRe..48.2043L. doi:10.1016/j.patcog.2014.12.020. hdl:10183/97001. (англ.)
- ↑ Fernandes, L.A.F.; Oliveira, M.M. (2012). A general framework for subspace detection in unordered multidimensional data. Pattern Recognition. 45 (9): 3566—3579. Bibcode:2012PatRe..45.3566F. doi:10.1016/j.patcog.2012.02.033. (англ.)
- ↑ Ballard, D.H. (1981). Generalizing the Houghtransform to detectarbitraryshapes. Pattern Recognition. 13 (2): 111—122. Bibcode:1981PatRe..13..111B. doi:10.1016/0031-3203(81)90009-1. hdl:1802/13802. (англ.)
- ↑ Vosselman, G., Dijkman, S: "3D Building Model Reconstruction from Point Clouds and Ground Plans", International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, vol 34, part 3/W4, October 22–24, 2001, Annapolis, MA, USA, pp. 37–44. (англ.)
- ↑ Tahir Rabbani: "Automatic reconstruction of industrial installations – Using point clouds and images" [Архівовано 2008-12-01 у Wayback Machine.], pages 43–44, Publications on Geodesy 62, Delft, 2006. ISBN 978-90-6132-297-9. (англ.)
- ↑ Achtert, Elke; Böhm, Christian; David, Jörn; Kröger, Peer; Zimek, Arthur (2008). Global Correlation Clustering Based on the Hough Transform. Statistical Analysis and Data Mining. 1 (3): 111—127. doi:10.1002/sam.10012. S2CID 5111283. (англ.)
- ↑ Tahir Rabbani and Frank van den Heuvel, "Efficient hough transform for automatic detection of cylinders in point clouds" in Proceedings of the 11th Annual Conference of the Advanced School for Computing and Imaging (ASCI '05), The Netherlands, June 2005. (англ.)
- ↑ Yonghong Xie; Qiang Ji (2002). A new efficient ellipse detection method. Object recognition supported by user interaction for service robots. Т. 2. с. 957—960. CiteSeerX 10.1.1.1.8792. doi:10.1109/ICPR.2002.1048464. ISBN 978-0-7695-1695-0. S2CID 9276255. (англ.)
- ↑ Image Transforms - Hough Transform. Homepages.inf.ed.ac.uk. Процитовано 17 серпня 2009. (англ.)
- hough_transform.cpp — код C++ — приклад бібліотеки CImg (бібліотека з відкритим кодом, первинний код C++, зображення у відтінках сірого)
- Інтерактивна демонстрація основ перетворення Гафа (англ.)
- https://web.archive.org/web/20070827233423/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/Hough.html — Java-аплет + первинник для вивчення перетворення Гафа у формі нахилу-відтину
- https://web.archive.org/web/20070827191440/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/HNF.html — Java-аплет + первинник для вивчення перетворення Гафа в нормальній формі
- http://www.sydlogan.com/deskew.html — Вирівнювання скосу зображень за допомогою перетворення Гафа (зображення у відтінках сірого, первинний код C++)
- https://web.archive.org/web/20070922090216/http://imaging.gmse.net/articledeskew.html — Вирівнювання скосу зображень за допомогою перетворення Гафа (первинний код Visual Basic)
- http://www.mitov.com/products/visionlab — Безкоштовна для освітніх цілей бібліотека Delphi, C++ та .NET, що містить складові перетворень Гафа для прямих, кіл та відрізків.
- Tarsha-Kurdi, F., Landes, T., Grussenmeyer, P., 2007a. Перетворення Хафа та розширені алгоритми RANSAC для автоматичного виявлення тривимірних площин даху будівлі з даних Лідара. ISPRS Proceedings. Семінар Лазерне сканування. Еспоо, Фінляндія, 12–14 вересня 2007 р.
- Into містить втілення перетворення Гафа з відкритим кодом C++ для прямих та кіл
- http://www.vision.ime.usp.br/~edelgado/defesa/code/hough.html Перетворення Гафа для виявляння еліпсів, втілене мовою C.
- scikit-image Перетворення Гафа для прямих, кіл та еліпсів, втілене мовою Python.
- Перетворення Гафа на основі вейвлетного фільтрування для виявляння кіл певного радіуса. (Код Matlab.)
- Перетворення Гафа для прямих із використанням MATLAB
- Перетворення Гафа для кіл у MATLAB
- KHT — первинний код C++.
- 3DKHT — первинний код C++ та набори даних.


 French
French Deutsch
Deutsch
































