Силогізм — Вікіпедія
Силогі́зм (грец. συλλογισμός — міркування) — міркування, що складається з трьох простих атрибутивних висловлювань: двох засновків і одного висновку. Засновок силогізму поділяють на більший (який містить предикат висновку) і менший (який містить суб'єкт висновку). За положенням середнього терміна силогізми поділяють на фігури, а останні за логічною формою засновків і висновку — на модуси.
Приклад силогізму:
- Усі люди смертні (більший засновок)
- Аристотель — людина (менший засновок)
- ------------
- Аристотель — смертний (висновок)
У силогізм входить рівно три терміни:
- S — менший термін: суб'єкт висновку (входить також у менший засновок);
- P — більший термін: предикат висновку (входить також у більший засновок);
- M — середній термін: входить в обидва засновки, але не входить у висновок.
Підмет S (суб'єкт) — те, щодо чого ми висловлюємось (ділиться на два види):
- Певний:
- Одиничне судження — в яких підмет є індивідуальним поняттям, на зразок «Ньютон відкрив закон тяжіння».
- Приватне судження — в якому підметом судження є поняття, взяте в частині свого обсягу, на зразок «Деякі S є P».
- Множинне судження — це ті, в яких є кілька підметів класових понять, на зразок «Комахи, павуки, раки — членистоногі».
- Непевний, на кшталт «світає», «боляче» тощо.
Присудок P (предикат) — те, що ми висловлюємо (2 види суджень):
- Розповідний — це судження щодо подій, станів, процесів або діяльності скороминущі, на зразок «Троянда в саду квітне».
- Описовий — коли одному або багатьом предметам приписується яка-небудь властивість. Суб'єктом завжди є певна річ, на зразок «Вогонь гарячий», «Сніг білий».
Відношення між підметом і присудком:
- Судження тотожності — поняття суб'єкта та предиката мають той самий обсяг, на зразок «Усякий рівносторонній трикутник є рівнокутним трикутником».
- Судження підпорядкування — поняття з менш широким обсягом підпорядковується поняттю з ширшим обсягом, на зразок «Собака — домашня тварина».
- Судження відношення — саме простору, часу, відносин, на зразок «Будинок знаходиться на вулиці».
При визначені відношення між підметом і присудком важливою є чітка формалізація термінів, оскільки бездомний собака хоч і не домашній з точки зору проживання в будинку, однаково належить до класу домашніх тварин з погляду належності за соціально-біологічною ознакою. Тобто слід розуміти, що «домашня тварина» із соціально-біологічної класифікації в окремих випадках може бути «недомашньою твариною» з погляду місця проживання, тобто із соціально-побутового погляду.
За якістю та кількістю розрізняють чотири види простих атрибутивних висловлювань:
- A — від лат. affirmo — загальноствердні («Всі люди смертні»)
- I — від лат. affirmo — частковоствердні («Деякі люди — студенти»)
- E — від лат. nego — загальнозаперечні («Жоден з китів не риба»)
- O — від лат. nego— частковозаперечні («Деякі люди не є студентами»)
Одиничні висловлювання (такі, в яких суб'єкт є одиничним терміном) дорівнюють загальним.
Суб'єкт завжди розподілений у загальному висловлюванні і ніколи не розподілений у частковому висловлюванні.
Предикат завжди розподілений у негативних думках, у ствердних він розподілений тоді, коли за обсягом Р≤S.
Як предикат, подекуди, може виступати суб'єкт.
- Середній термін має бути розподілений хоча би в одному із засновків.
- Термін, нерозподілений у засновку, не має бути розподіленим у висновку.
- Кількість негативних засновків має дорівнювати кількості негативних висновків.
- У кожному силогізмі має бути тільки три терміни.
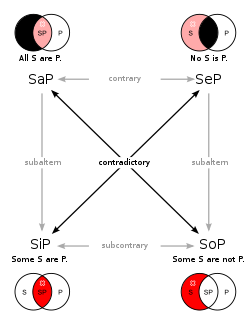
(Темні зони — порожні,
червоні — не порожні.)
Фігурами силогізму називають форми силогізму, які відрізняються позицією середнього терміна в засновках:
| Фігура 1 | Фігура 2 | Фігура 3 | Фігура 4 | |||||
| Більший засновок: | M—P | P—M | M—P | P—M | ||||
| Менший засновок: | S—M | S—M | M—S | M—S | ||||
| Висновок: | S—P | S—P | S—P | S—P |
Кожній фігурі відповідають модуси — форми силогізму, які відрізняються кількістю та якістю засновків і висновків. Модуси вивчали ще середньовічні школи, і для правильних модусів кожній фігурі було вигадано мнемонічні імена (Наведіть курсор, щоб побачити приклади): Переважна більшість із 256 можливих форм силогізму є недійсними (висновок не випливає логічно із засновків). Наведена нижче таблиця показує допустимі форми, та навіть деякі з цих іноді вважаються такими, що призводять до екзистенційної помилки, тобто вони є недійсними, якщо вони згадують порожні категорії. Ці спірні моделі виділено курсивом.
| Фігура 1 | Фігура 2 | Фігура 3 | Фігура 4 |
| Barbara | Cesare | Datisi | Calemes |
| Celarent | Camestres | Disamis | Dimatis |
| Darii | Festino | Ferison | Fresison |
| Ferio | Baroco | Bocardo | Calemos |
| Barbari | Cesaro | Felapton | Fesapo |
| Celaront | Camestros | Darapti | Bamalip |
 Barbara |  Celarent |  Darii |  Ferio |  Barbari |  Celaront |
 Cesare |  Camestres |  Festino |  Baroco |  Cesaro |  Camestros |
 Datisi |  Disamis |  Ferison |  Bocardo |  Felapton |  Darapti |
 Calemes |  Dimatis |  Fresison |  Calemos |  Fesapo |  Bamalip |
Відповідно до правил, форми можна перетворити на інші форми, та всі форми можна перетворити на одну з форм першої фігури.
Учення про силогізм уперше виклав Аристотель у його «Першій аналітиці». Він говорить лише про три фігури категоричного силогізму, не згадуючи про можливу четверту. Особливо докладно він розглядає роль модальності суджень у процесі умовиводу. Наступник Арістотеля, засновник ботаніки Теофраст, за словами Олександра Афродізійського (у його коментарі до першої «Аналітика» Аристотеля), додав ще п'ять модусів (modi) до першої фігури силогізму; ці п'ять модусів згодом були виділені Клавдієм Галеном (жив у II-му ст. н. е.) в особливу четверту фігуру. Крім того, Теофраст і його учень Евдем зайнялися аналізом умовного і роздільного силогізмів. Вони допустили п'ять видів умовиводів: два з них відповідають умовному С., а три — роздільному, який вони розглядали як видозміну умовного С. Цим і закінчується розвиток вчення про С. в давнину, якщо не рахувати того додатку, що зробили стоїки у вченні про умовний С. За словами Секста Емпірика, стоїки визнавали деякі види умовного і роздільного силогізму (грец. αναπόδεικτοι), тобто що не потребують доказів, і розглядали їх як прототипи С. (як, наприклад, нині дивиться на С. Зігварт). Стоїки визнавали п'ять видів подібних С., що збігаються з Феофрастовими. Секст Емпірика наводить такі приклади для цих п'яти видів.
- Якщо настав день, то є світло, але тепер день, а отже є світло.
- Якщо настав день, то є світло, але світла немає, а отже немає й дня.
- Не може бути (одночасно) дня і ночі, але день настав, отже, немає ночі.
- Може бути або день, чи ніч, але тепер день, отже, немає ночі.
- Може бути або день, чи ніч, але ночі нема, отже, тепер день .
У Секста Емпірика і скептиків взагалі ми зустрічаємося і з критикою С., але мета критики — доказ неможливості доказу взагалі, у тому числі і силогістичного. Схоластична логіка нічого суттєвого не додала до навчання про силогізм; вона лише порвала той зв'язок з теорією пізнання, яка існувала в Аристотеля і тим перетворила логіку в чисто формальне вчення. Зразковим керівництвом логіки в середні віки був твір Марціана Капели, зразковим коментарем — твори Боеція. Деякі з коментарів Боеція займаються спеціально вченням про С., напр. «Introductio ad categoricos syllogismes», «De syllogisme categorico» і «De syllogismo hypothetico». Твори Боеція мають деяке історичне значення; вони сприяли також встановленню логічної термінології. Але в той же самий час саме Боецій надав навчанням логічним характер чисто формальний.
З епохи схоластичної філософії по відношенню до вчення про С. уваги заслуговує Фома Аквінський (1274), особливо його докладний аналіз помилкових висновків («De fallaciis»). Твори з логіки, мали деяке історичне значення, належить візантійцеві Михайлу Пселу. Він запропонував так званий «логічний квадрат», в якому наочно виражається ставлення різних видів суджень. Йому належать назви різних modi (грец. τρόποι) фігур. Ці назви, латинізовані, перейшли до західної логічної літератури.
Михайло Псел, слідуючи Феофрасу, п'ять modi четвертої фігури відносив до першого. Назва видів у нього мала на увазі мнемонічну мету. Йому ж належить і загальновживане позначення літерами кількості та якості суджень (а, е, i, о). Логічні вчення у Псела мають формальний характер. Твір Псела було переведено Вільгельмом Ширвудом, він набув поширення завдяки переробці Петра Іспанського (папи Івана XXI). У Петра Іспанського в його підручнику помітно те ж прагнення до мнемотехнічних правил. Латинські назви видів фігур, які приводяться в формальній логіці, взяті у Петра Іспанського. Петро Іспанський і Михайло Псьол являють собою розквіт формальної логіки в середньовічній філософії. З епохи Відродження починається критика формальної логіки і силогістичного формалізму.
Першим серйозним критиком Аристотелівської логіки був П'єр Рамі, який загинув під час Варфоломеєвської ночі. У другій частині його «Діалектики» йдеться про С.; його вчення про С., проте, істотних відступів від Арістотеля не представляє. Починаючи з Бекона і Декарта філософія йде за новими шляхами і відстоює методи дослідження: непридатність силогістичного методу в сенсі методу дослідження, знаходження істини, стає все більш і очевиднішим.
«…Винахід силогістичної форми є одним з найпрекрасніших і навіть найважливіших відкриттів людського духу, — говорить Г. В. Лейбніц. Це — свого роду універсальна математика, все значення якої ще недостатньо зрозуміле».
Силогізм переважав у логіці до XIX століття і мав обмежене застосування, зокрема через прив'язку до категоричного силогізму. Заміною силогізму служить простіша та потужна логіка першого порядку, а також теорія кванторів.
Аксіома силогізму — положення, яке обґрунтовує правомірність висновку із засновків. Все, що стверджується про клас можна стверджувати про кожен предмет класу. Тобто, ознака ознаки речі є ознакою самої речі.
- Яценко С. С. Софістика / Київ. : ТОВ «Сік Груп Україна», 2016, 208 с. ISBN 978-617-7092-95-6
- Філософський словник / за ред. В. І. Шинкарука. — 2-ге вид., перероб. і доп. — К. : Головна ред. УРЕ, 1986.
- Модуси силогізму // Філософський енциклопедичний словник / В. І. Шинкарук (гол. редкол.) та ін ; Інститут філософії імені Григорія Сковороди НАН України. — Київ : Абрис, 2002. — С. 393. — 742 с. — 1000 екз. — ББК 87я2. — ISBN 966-531-128-X.
- І.Алексюк. Силогізм // ФЕС, с.578
- Категоричне судження // Літературознавча енциклопедія : у 2 т. / авт.-уклад. Ю. І. Ковалів. — Київ : ВЦ «Академія», 2007. — Т. 1 : А — Л. — С. 467.
- 388; 419/mode/1up?view=theater Правила простого категоричного силогізму; Силогізм; Сорит // Літературознавча енциклопедія : у 2 т. / авт.-уклад. Ю. І. Ковалів. — Київ : ВЦ «Академія», 2007. — Т. 2 : М — Я. — С. 262; 388; 419.


 French
French Deutsch
Deutsch