Тригонометричні функції — Вікіпедія

Тригонометричні функції
Досліджується в	тригонометрія
Апроксимаційний алгоритм	CORDIC
Підтримується Вікіпроєктом	Вікіпедія:Проєкт:Математика
Обернений елемент	обернені тригонометричні функції
Тригонометричні функції у Вікісховищі

Тригонометрія
Обрис[en] Історія Застосування[en] Функції (обернені) Полігонометрія
Посилання
Тотожності Точні сталі Таблиці[en] Одиничне коло
Закони і теореми
Синуси Косинуси Тангенси Котангенси Теорема Піфагора
Обчислення
Тригонометричні підстановки[en] Інтеграли (обернені функції) Похідні
п о р

Тригонометри́чні фу́нкції — функції кута. Вони можуть бути визначені як відношення двох сторін та кута трикутника або як відношення координат точок кола. Відіграють важливу роль при дослідженні періодичних функцій та багатьох об'єктів. Наприклад, при дослідженні рядів, диференціальних рівнянь.

Наведемо шість базових тригонометричних функцій. Останні чотири визначаються через перші дві. Іншими словами, вони є означеннями, а не самостійними сутностями.

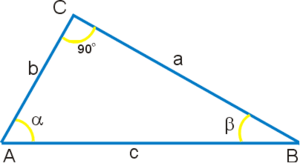
• синус (${\displaystyle \sin \alpha }$);
• косинус (${\displaystyle \cos \alpha }$);
• тангенс (${\displaystyle \operatorname {tg} \alpha ={\tfrac {\sin \alpha }{\cos \alpha }}}$);
• котангенс (${\displaystyle \operatorname {ctg} \alpha ={\tfrac {\cos \alpha }{\sin \alpha }}}$);
• секанс (${\displaystyle \sec \alpha ={\tfrac {1}{\cos \alpha }}}$);
• косеканс (${\displaystyle \operatorname {cosec} \alpha ={\tfrac {1}{\sin \alpha }}}$);

Тригонометричні функції можна визначити розглянувши прямокутний трикутник.
Косинусом кута називається відношення довжини прилеглого катета до довжини гіпотенузи:

${\displaystyle \cos \alpha ={\frac {AC}{AB}}={\frac {b}{c}},~~~\cos \beta ={\frac {BC}{AB}}={\frac {a}{c}}~.}$

Синусом кута називається відношення довжини протилежного катета до довжини гіпотенузи:

${\displaystyle \sin \alpha ={\frac {BC}{AB}}={\frac {a}{c}},~~~\sin \beta ={\frac {AC}{AB}}={\frac {b}{c}}~.}$

Тангенсом кута називається відношення довжини протилежного катета до довжини прилеглого катета:

${\displaystyle \operatorname {tg} \alpha ={\frac {BC}{AC}}={\frac {a}{b}},~~~\operatorname {tg} \beta ={\frac {AC}{BC}}={\frac {b}{a}}~.}$

Котангенсом кута називається відношення довжини прилеглого катета до довжини протилежного катета:

${\displaystyle \operatorname {ctg} \alpha ={\frac {AC}{BC}}={\frac {b}{a}},~~~\operatorname {ctg} \beta ={\frac {BC}{AC}}={\frac {a}{b}}~.}$

Аналогічним чином можна визначити тригонометричні функції на колі з одиничним радіусом.

${\displaystyle \sin x}$ та ${\displaystyle \cos x}$ — це періодичні функції із періодом ${\displaystyle \ 2\pi }$,
${\displaystyle \operatorname {tg} x}$ та ${\displaystyle \operatorname {ctg} x}$ мають період ${\displaystyle \ \pi .}$

Співвідношення, наведені нижче, дозволяють виразити значення тригонометричних функцій від довільного дійсного арґументу через значення функцій для аргументу з інтервалу ${\displaystyle \left[0,{\pi \over 2}\right]}$

${\displaystyle \sin x=\cos \left({\pi \over 2}-x\right)}$

${\displaystyle \cos x=\sin \left({\pi \over 2}-x\right)}$

${\displaystyle \operatorname {tg} x=\operatorname {ctg} \left({\pi \over 2}-x\right)}$

${\displaystyle \operatorname {ctg} x=\operatorname {tg} \left({\pi \over 2}-x\right)}$

Наступне співвідношення випливає із теореми Піфагора:

${\displaystyle ~\sin ^{2}x+\cos ^{2}x=1}$

З основного співвідношення

${\displaystyle \sin {\left(\alpha +\beta \right)}=\sin \alpha \cos \beta +\cos \alpha \sin \beta }$

отримуємо

${\displaystyle \sin {\left(\alpha \pm \beta \right)}=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta ,}$

${\displaystyle \cos {\left(\alpha \pm \beta \right)}=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta ,}$

${\displaystyle \operatorname {tg} {\left(\alpha \pm \beta \right)}={{\operatorname {tg} \alpha \pm \operatorname {tg} \beta } \over {1\mp \operatorname {tg} \alpha \operatorname {tg} \beta }},~~~\operatorname {ctg} {\left(\alpha \pm \beta \right)}={{\operatorname {ctg} \alpha \operatorname {ctg} \beta \mp 1} \over {\operatorname {ctg} \beta \pm \operatorname {ctg} \alpha }}}$

${\displaystyle \sin {2\alpha }=2\sin \alpha \cos \alpha }$

${\displaystyle \cos {2\alpha }=\cos ^{2}\alpha -\sin ^{2}\alpha =2\cos ^{2}\alpha -1=1-2\sin ^{2}\alpha }$

${\displaystyle \operatorname {tg} {2\alpha }={{2\operatorname {tg} \alpha } \over {1-\operatorname {tg} ^{2}\alpha }}~,~~~\operatorname {ctg} {2\alpha }={{\operatorname {ctg} ^{2}\alpha -1} \over {2\operatorname {ctg} \alpha }}={1 \over 2}{\left(\operatorname {ctg} \alpha -\operatorname {tg} \alpha \right)}}$

${\displaystyle \sin {3\alpha }=3\sin \alpha -4\sin ^{3}\alpha ~,~~~\cos {3\alpha }=4\cos ^{3}\alpha -3\cos \alpha }$

${\displaystyle \sin {\alpha \over 2}={\sqrt {{1-\cos \alpha } \over 2}}~,~~~\cos {\alpha \over 2}={\sqrt {{1+\cos \alpha } \over 2}}}$

${\displaystyle \operatorname {tg} {\alpha \over 2}={\sin \alpha \over {1+\cos \alpha }}={{1-\cos \alpha } \over \sin \alpha }~,~~~\operatorname {ctg} {\alpha \over 2}={\sin \alpha \over {1-\cos \alpha }}={{1+\cos \alpha } \over \sin \alpha }}$

${\displaystyle a\sin A+b\cos A=r\sin {\left(A+B\right)}=r\cos \left({\pi \over 2}-A-B\right)={\sqrt {a^{2}+b^{2}}}\sin {\left(A+\operatorname {arctg} {b \over a}\right)},~{r={\sqrt {a^{2}+b^{2}}}},~{tgB={b \over a}}}$

${\displaystyle \sin A\pm \sin B=2\sin {{A\pm B} \over 2}\cos {{A\mp B} \over 2}}$

${\displaystyle \cos A+\cos B=2\cos {{A+B} \over 2}\cos {{A-B} \over 2}}$

${\displaystyle \cos A-\cos B=-2\sin {{A+B} \over 2}\sin {{A-B} \over 2}}$

${\displaystyle \operatorname {tg} A\pm \operatorname {tg} B={\sin {A\pm B} \over {\cos A\cos B}}~,~~\operatorname {ctg} A\pm \operatorname {ctg} B={\sin {B\pm A} \over {\sin A\sin B}}}$

Формула для суми будь-якої кількості синусів кутів із їх зсувом і отримання однієї функції кута:

${\displaystyle A\sin(x+\alpha )+B\sin(x+\beta )+C\sin(x+\gamma )+...=Y\sin x+Z\cos x={\sqrt {Y^{2}+Z^{2}}}\sin(x+\operatorname {arctg} {Z \over Y}),~{Y=A\cos(\alpha )+B\cos(\beta )+C\cos(\gamma )+...},~{Z=A\sin(\alpha )+B\sin(\beta )+C\sin(\gamma )+...}}$

Якщо ${\displaystyle n}$ є цілим додатним числом, то

${\displaystyle \sin {nA}={n \choose 1}\cos ^{n-1}A\sin A-{n \choose 3}\cos ^{n-3}A\sin ^{3}A+{n \choose 5}\cos ^{n-5}A\sin ^{5}A\mp \cdots }$

${\displaystyle \cos {nA}=\cos ^{n}A-{n \choose 2}\cos ^{n-2}A\sin ^{2}A+{n \choose 4}\cos ^{n-4}A\sin ^{4}A\mp \cdots }$

Якщо n є цілим непарним числом, то

${\displaystyle \sin ^{n}x={{(-1)^{{n-1} \over 2}} \over {2^{n-1}}}\left[\sin {nx}-{n \choose 1}\sin {(n-2)x}+{n \choose 2}\sin {(n-4)x}-{n \choose 3}\sin {(n-6)x}+\cdots +(-1)^{{n-1} \over 2}{n \choose {{n-1} \over 2}}\sin x\right]}$

${\displaystyle \cos ^{n}x={\left({1 \over 2}\right)}^{n-1}\left[\cos {nx}+{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}+{n \choose 3}\cos {(n-6)x}+\cdots +{n \choose {{n-1} \over 2}}\cos x\right]}$

Якщо n є цілим парним числом, то

${\displaystyle \sin ^{n}x={{{\left(-1\right)}^{n \over 2}} \over {2^{n-1}}}\left[\cos {nx}-{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}-{n \choose 3}\cos {(n-6)x}+\cdots +{\left(-1\right)}^{{n-2} \over 2}{n \choose {{n-2} \over 2}}\cos {2x}\right]+{1 \over 2^{n}}{n \choose {n \over 2}}}$

${\displaystyle \cos ^{n}x={\left({1 \over 2}\right)}^{n-1}\left[\cos {nx}+{n \choose 1}\cos {(n-2)x}+{n \choose 2}\cos {(n-4)x}+{n \choose 3}\cos {(n-6)x}+\cdots +{n \choose {{n-2} \over 2}}\cos {2x}\right]+{1 \over 2^{n}}{n \choose {n \over 2}}}$

Існують такі розклади в ряд Тейлора тригонометричних функцій:

${\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}}}$

${\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}}$

${\displaystyle {\begin{aligned}\operatorname {tg} x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n+1}x^{2n+1}}{(2n+1)!}}\\&{}=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+{\frac {17x^{7}}{315}}+{\frac {62x^{9}}{2835}}+\cdots ,\qquad {\text{при }}|x|<{\frac {\pi }{2}}\end{aligned}}}$

де

${\displaystyle U_{n}}$ — n-те перетворення Бустрофедона,

${\displaystyle B_{n}}$ — числа Бернуллі, та

${\displaystyle E_{n}}$ — числа Ейлера.

${\displaystyle {\begin{aligned}\operatorname {cosec} x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}2(2^{2n-1}-1)B_{2n}x^{2n-1}}{(2n)!}}\\&{}={\frac {1}{x}}+{\frac {x}{6}}+{\frac {7x^{3}}{360}}+{\frac {31x^{5}}{15120}}+\cdots ,\qquad {\text{при }}0<|x|<\pi \end{aligned}}}$

${\displaystyle {\begin{aligned}\sec x&{}=\sum _{n=0}^{\infty }{\frac {U_{2n}x^{2n}}{(2n)!}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}x^{2n}}{(2n)!}}\\&{}=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+{\frac {61x^{6}}{720}}+\cdots ,\qquad {\text{при }}|x|<{\frac {\pi }{2}}\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {ctg} x&{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}2^{2n}B_{2n}x^{2n-1}}{(2n)!}}\\&{}={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-\cdots ,\qquad {\text{при }}0<|x|<\pi \end{aligned}}}$

Використовуючи вищенаведені розклади в ряди Тейлора можна показати, що функції ${\displaystyle \sin }$ та ${\displaystyle \cos }$ є уявною та дійсною частинами експоненти чисто уявного числа:

${\displaystyle e^{i\theta }=\cos \theta +i\sin \theta .\,}$

Це співвідношення називається формулою Ейлера.

Можна визначити тригонометричні функції комплексної змінної z:

${\displaystyle \sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}\,=\,{e^{iz}-e^{-iz} \over 2i}=-i\operatorname {sh} \left(iz\right),}$

${\displaystyle \cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}\,=\,{e^{iz}+e^{-iz} \over 2}=\operatorname {ch} \left(iz\right)}$

де ${\displaystyle i^{2}=-1}$, а ${\displaystyle \operatorname {sh} x}$ та ${\displaystyle \operatorname {ch} x}$ — відповідно гіперболічні синус та косинус. Для дійсного ${\displaystyle x}$ мають місце співвідношення

${\displaystyle \cos x=\operatorname {Re} (e^{ix})~,~~~~\sin x=\operatorname {Im} (e^{ix})}$

${\displaystyle \ \ \ \ f(x)}$	${\displaystyle {\frac {d}{dx}}f(x)}$	${\displaystyle \int f(x)\,dx}$
${\displaystyle \,\ \sin x}$	${\displaystyle \,\ \cos x}$	${\displaystyle \,\ -\cos x+C}$
${\displaystyle \,\ \cos x}$	${\displaystyle \,\ -\sin x}$	${\displaystyle \,\ \sin x+C}$
${\displaystyle \,\ \operatorname {tg} x}$	${\displaystyle \,\ \sec ^{2}x}$	${\displaystyle -\ln \left|\cos x\right|+C}$
${\displaystyle \,\ \operatorname {ctg} x}$	${\displaystyle \,\ -\operatorname {cosec} ^{2}x}$	${\displaystyle \ln \left|\sin x\right|+C}$
${\displaystyle \,\ \sec x}$	${\displaystyle \,\ \sec {x}\operatorname {tg} {x}}$	${\displaystyle \ln \left|\sec x+\operatorname {tg} x\right|+C}$
${\displaystyle \,\ \operatorname {cosec} x}$	${\displaystyle \,\ -\operatorname {cosec} {x}\operatorname {ctg} {x}}$	${\displaystyle -\ln \left|\operatorname {cosec} x+\operatorname {ctg} x\right|+C}$

Функції ${\displaystyle \sin \,x}$ та ${\displaystyle \cos \,x}$ є розв'язками диференціального рівняння гармонічних коливань

${\displaystyle {d^{2}y \over d{x^{2}}}+y=0}$

Теорема синусів стверджує, що для довільного трикутника зі сторонами ${\displaystyle a}$, ${\displaystyle b}$, і ${\displaystyle c}$ та кутами, що протилежні тим сторонам ${\displaystyle A}$, ${\displaystyle B}$ і ${\displaystyle C}$:

${\displaystyle {\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}}={\frac {2\Delta }{abc}},}$

де ${\displaystyle \Delta }$ — це площа трикутника, або, еквівалентно,

${\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R,}$

де ${\displaystyle R}$ — це радіус кола, що описує трикутник.

Це можна довести розділивши трикутник на два прямокутних трикутники, і використовуючи визначення синуса. Теорема синусів корисна для розрахунку довжин невідомих сторін трикутника, при відомих двох кутах і довжині однієї з його сторін. Ця ситуація є типовою для задачі триангуляції, техніки визначення невідомих відстаней шляхом вимірювання двох кутів із двох точок на доступній відомій відстані.

Теорема косинусів є узагальненням теореми Піфагора:

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C,\,}$

або еквівалентно,

${\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}.}$

В цій формулі кут ${\displaystyle C}$ є протилежним до сторони ${\displaystyle c}$. Цю теорему можна довести розділивши трикутник на два прямокутних трикутники та застосувавши теорему Піфагора.

Теорему косинусів можна застосувати для визначення сторони трикутника, якщо відомі довжини двох сторін і кут між ними. Також її можна застосувати для визначення косинуса кута (і відповідно значення самого кута) якщо відомі довжини всіх сторін трикутника.

Всі наступні вирази формулюють теорему тангенсів^[1]

${\displaystyle {\frac {\operatorname {tg} {\dfrac {A-B}{2}}}{\operatorname {tg} {\dfrac {A+B}{2}}}}={\frac {a-b}{a+b}}\,;\qquad {\frac {\operatorname {tg} {\dfrac {A-C}{2}}}{\operatorname {tg} {\dfrac {A+C}{2}}}}={\frac {a-c}{a+c}}\,;\qquad {\frac {\operatorname {tg} {\dfrac {B-C}{2}}}{\operatorname {tg} {\dfrac {B+C}{2}}}}={\frac {b-c}{b+c}}}$

Пояснення цих формул на словах було б громіздким, але закономірності сум і різниць для довжин сторін і відповідних протилежних кутів видно із теореми.

Якщо

${\displaystyle \zeta ={\sqrt {{\frac {1}{s}}(s-a)(s-b)(s-c)}}\ }$ (радіус вписаного кола в трикутник)

і

${\displaystyle s={\frac {a+b+c}{2}}\ }$ (напівпериметр трикутника),

тоді всі наступні формули описують теорему котангенсів^[1]

${\displaystyle \operatorname {ctg} {\frac {A}{2}}={\frac {s-a}{\zeta }}\,;\qquad \operatorname {ctg} {\frac {B}{2}}={\frac {s-b}{\zeta }}\,;\qquad \operatorname {ctg} {\frac {C}{2}}={\frac {s-c}{\zeta }}}$

Звідси випливає, що

${\displaystyle {\frac {\operatorname {ctg} {\dfrac {A}{2}}}{s-a}}={\frac {\operatorname {ctg} {\dfrac {B}{2}}}{s-b}}={\frac {\operatorname {ctg} {\dfrac {C}{2}}}{s-c}}.}$

На словах теорема полягає в тому, що котангенс половинного кута дорівнює відношенню напівпериметра від якого віднято сторону протилежну заданому куту, до радіуса вписаного кола.

Тригонометричні функції також мають важливе застосування у фізиці. Функції синуса і косинуса, наприклад, використовують для описання гармонічних коливань, які моделюють багато природних явищ, такі як рух маси закріпленої на пружині, і для малих кутів, рух маятника для маси що висить на нитці. Функції синуса і косинуса є одновимірними проєкціями рівномірного кругового руху.

Тригонометричні функції також довели свою користь при вивченні загальних періодичних функцій. Характерна хвильова структура періодичних функцій корисна для моделювання явищ, таких як звукові або світлові хвилі.^[2]

В загальних умовах, періодичну функцію ${\displaystyle f(x)}$ можна виразити у вигляді суми синусних або косинусних хвиль за допомогою Ряду Фур'є.^[3] Позначивши синусні або косинусні базисні функції як ${\displaystyle \varphi _{k}}$, розкладання періодичної функції ${\displaystyle f(x)}$ буде мати наступну форму:

${\displaystyle f(t)=\sum _{k=1}^{\infty }c_{k}\varphi _{k}(t).}$

Наприклад, квадратну хвилю (меандр) можна записати у вигляді ряду Фур'є

${\displaystyle f_{\text{square}}(t)={\frac {4}{\pi }}\sum _{k=1}^{\infty }{\sin {\big (}(2k-1)t{\big )} \over 2k-1}.}$

В анімації квадратної хвилі праворуч можна побачити, що лише декілька термів вже досить аби створити добру апроксимацію квадратної форми хвилі. Суперпозицію декількох термів в розкладанні пилоподібної хвилі можна побачити знизу під тим малюнком.

• Обернені тригонометричні функції
• Екзотичні тригонометричні функції
• Список тригонометричних тотожностей
• Таблиця інтегралів тригонометричних функцій
• Інтегральні тригонометричні функції
• Тригонометрія
• Координатний транспортир
• Тригонометричне рівняння

• Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973, — 832 с.
• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2024. — 2403 с.(укр.)

• Тангенс // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
• Тригонометричні функції // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 180. — 594 с.
• FIZMA.neT - Математика онлайн [Архівовано 1 квітня 2022 у Wayback Machine.]
• Тригонометричні формули. OnlineMSchool. Архів оригіналу за 3 березня 2021. Процитовано 13 лютого 2021.