Сортування гребінцем — Вікіпедія

Ця стаття містить правописні, лексичні, граматичні, стилістичні або інші мовні помилки, які треба виправити. Ви можете допомогти вдосконалити цю статтю, погодивши її із чинними мовними стандартами. (липень 2020)

Сортування гребінцем

Клас	Алгоритм сортування
Структура даних	масив
Найгірша швидкодія	${\displaystyle \Omega (n^{2})}$[1]
Найкраща швидкодія	${\displaystyle O(n)}$
Середня швидкодія	${\displaystyle \Omega (nlogn)}$
Просторова складність у найгіршому випадку	О(n) загальний, O(1) допоміжний
Оптимальний	Так

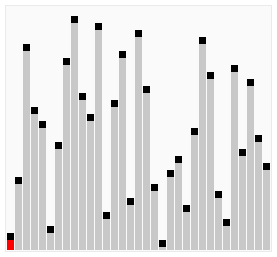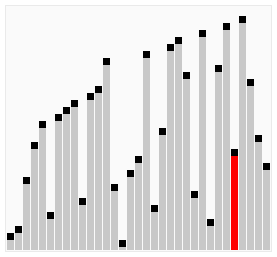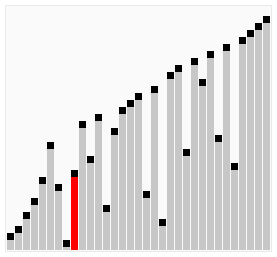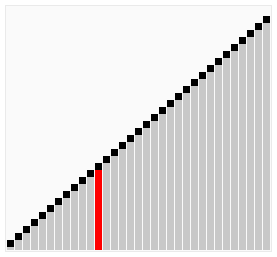
Сортування гребінцем (англ. Comb sort) — спрощений алгоритм сортування, розроблений Влодеком Добошєвічем (Wlodek Dobosiewicz) у 1980 році, і пізніше заново дослідженим та популяризованим Стефаном Лакеєм (Stephen Lacey) та Річардом Боксом (Richard Box), котрі написали про нього в журналі Byte Magazine у квітні 1991 р. Сортування гребінцем є поліпшенням алгоритму сортування бульбашкою, і конкурує у швидкодії з алгоритмом Швидке сортування. Основна його ідея полягає в тому, щоб усунути так званих «черепах», або малих значень ближче до кінця списку, оскільки у сортування бульбашкою вони сильно уповільнюють процес сортування. (Кролики та великі сортування на початку списку у сортуванні бульбашкою не являють собою проблеми).

У сортуванні бульбашкою, коли два елементи порівнюються, вони завжди мають розрив (відстань один від одного) рівну 1. Основна ідея сортування гребінцем полягає у тому, що цей розрив може бути більший одиниці. (Алгоритм Сортування Шелла також базується на даній ідеї, однак, він є модифікацією алгоритму сортування включенням, а не сортування бульбашкою).

Розрив починається зі значення, що рівне довжині списку, поділеного на фактор зменшення (зазвичай, 1.3; див. нижче), і список сортується з урахуванням цього значення (при необхідності воно заокруглюється до цілого). Потім розрив знову ділиться на фактор розриву, і список продовжує сортуватись з новим значенням, процес продовжується доти, доки розрив рівний 1. Далі список сортується з розривом рівним 1 доти, доки не буде повністю відсортований. Таким чином, фінальний етап сортування аналогічний такому ж у сортуванні бульбашкою, однак, до цього «черепахи» усуваються.

Фактор зменшення справляє великий ефект на швидкість алгоритму сортування гребінцем. В оригінальній статті, автор пропонує значення 1.3 після багатьох експериментів з іншими значеннями.

Текст описує процес вдосконалення алгоритму використовуючи значення ${\displaystyle 1/\left(1-{\frac {1}{e^{\varphi }}}\right)\approx 1.247330950103979}$ як фактор зменшення. Вона також мість приклад використання алгоритму на псевдокоді.

function combsort11(array input)     gap := input.size 

    loop until gap > 1 and swaps = 1         if gap > 1             gap := gap / 1.3         end if         
         i := 0         swaps := 0         
         loop until i + gap <= input.size             if input[i] > input[i+gap]                 swap(input[i], input[i+gap])                 swaps := 1             end if             i := i + 1         end loop        
     end loop end function 

int newGap(int gap) {     gap /= 1.3;     if (gap < 1)         return 1;      return gap; }  void combSort(int* a, int len) {     int gap = len;     bool swapped = true;      while (gap > 1 || swapped)     {         swapped = false;         gap = newGap(gap);          for (int i = 0; i < len - gap; ++i)         {             if (a[i] > a[i + gap])             {                 swap(a[i], a[i + gap]);                 swapped = true;             }         }     } } 

private static int newGap(int gap) {         gap = gap * 10 / 13;         if(gap < 1)                 return 1;          return gap; }  private static void sort(int a[]) {       int gap = a.length;         boolean swapped;          do {                 swapped = false;                 gap = newGap(gap);  		for(int i = 0; i < (a.length - gap); i++) { 			if(a[i] > a[i + gap]){ 		        	swapped = true;                                 int temp = a[i];                                 a[i] = a[i + gap];                                 a[i + gap] = temp;                         }                 }         } while(gap > 1 || swapped); } 

def update_gap(gap):     gap = (gap * 10) / 13     if gap == 9 or gap == 10:         gap = 11     return max(1, gap)  def combsort(x):     gap = len(x)     swapped = True     if gap < 2:         return     while gap > 1 or swapped:         gap = update_gap(gap)         swapped = False         for i in range(0, len(x) - gap, gap):             if x[i] > x[i + gap]:                 x[i], x[i + gap] = x[i + gap], x[i]                 swapped = True 

• Сортування бульбашкою
• Сортування змішуванням