Коренуване – Уикипедия
Корен -ти от числото в математиката се нарича такова число че . [1] Символът се нарича радикал. Числото се нарича коренен показател (показател на корена), индекс или степен на корена. Той е естествено число, по-голямо или равно на 2, защото случаят е тривиален и не представлява интерес. Числото най-често е реално или комплексно число, но има и обобщения за други математически обекти, например остатъци, матрици и оператори. Изчисляването на корен от число се нарича коренуване.
В математическия анализ корените се считат за специален случай на степенуване, където степента е дроб: .
Общоприето е корен 2-ри да се нарича квадратен корен, а корен 3-ти – кубичен корен. Обикновено показателят на квадратния корен не се записва и ако не е отбелязан, се подразбира . Например:
- Квадратен корен от 9 са 3 и −3, защото 32 = 9 и (−3)2 = 9, или .
- защото
При всеки четен коренен показател се получават 2 корена, които са еднакви числа с обратни знаци, както се вижда от първия пример. За еднозначно определяне е въведено понятието аритметичен корен, чиято стойност винаги е неотрицателна, в първия пример това е числото 3.
Всяко реално или комплексно число има на брой комплексни корени. Корените от 0 са винаги 0.
Няма реални корени с четна степен от отрицателни числа. Винаги е възможно да се извлече корен с произволна степен от комплексно число, но резултатът не е еднозначно определен – комплексен -ти корен от число, различно от нула има различни стойности.
Корените са особено важни в теорията на безкрайните редове. -тите корени могат да бъдат дефинирани в областта на комплексните числа, а комплексните корени от 1 играят важна роля във висшата математика.

История
[редактиране | редактиране на кода]
(около 1800 – 1600 г. пр. н.е.) с изчисления
Първите задачи, свързани с извличането на квадратния корен, са намерени в трудовете на вавилонските математици. Сред тези задачи са:[2]
- Приложението на теоремата на Питагор за намирането на страните на правоъгълен триъгълник по вече известни други две страни.
- Намирането на страните на квадрат с известна площ.
- Решаването на квадратни уравнения.
Вавилонските математици разработват специален числен метод за извличането на квадратен корен. Първоначалното приближение за се изчислява, изхождайки от най-близкото до корена (от по-малката страна) естествено число . Представяйки подкоренния израз във вида , се получава , след което се използва повтарящ се процес за прецизност, съответстващ на метода на Нютон:[3]
Итерациите в този метод имат много бърза сходимост. За , например, се получава последователно приближение:
Всичките цифри, освен последната, са верни.
Аналогични задачи и методи се срещат в древнокитайската „Математика в девет книги“.[4] Древните гърци правят важното откритие, че е ирационално число. Детайлно изследване, водено от Таетет Афински (IV век пр. н.е.), показва, че ако коренът на естествено число не е цяло число, то той ирационален.[5]
Гърците формулират проблема за удвояването на куба, който се свежда до построяването на кубичен корен с помощта на линийка и пергел. Проблемът се оказва неразрешим. Алгоритмите за намирането на кубичния корен публикуват Херон (I век) и индийският математик Ариабхата (V в.).
Алгоритмите за извличане на корен от коя да е степен от цяло число, разработени от индийски и ислямски математици, са усъвършенствани в средновековна Европа. Епископът Николай Орем (род. 1330 год. Фльори Сюр Орн, кралство Франция - поч. 1382 год. Лизио, кралство Франция) първи изтълкува корена от -та степен като повдигане на степен .[6]
След появяването на формулата на Кардано (XVI век) започва използването на имагинерни числа в математиката, считани за квадратните корени на отрицателните числа.[7] Основите на техниката за работа с комплексни числа са разработени в началото на XIX век от Рафаел Бомбели, който предлага първоначалния метод за изчисляване с корени (с помощта на верижни дроби). Откриването на формулата на Моавър (1707 г.) показва, че намирането на корен от коя да е степен от комплексно число винаги е възможно и не води до нов тип числа.[8]
Комплексните корени от произволна степен са дълбоко изследвани от Гаус в началото на XIX век, въпреки че първите резултати принадлежат на Ойлер.[9]

Определение и свързани понятия
[редактиране | редактиране на кода]Освен приведеното по-горе, може да се дадат две равносилни определения на корена:[10]
- Корен -ти от число е решението на уравнението (имайки предвид, че решенията могат да са няколко или николко)
- Корен -ти от число е коренът на многочлена , тоест стойността , при която даденият многочлен е равен на нула.
Операцията по изчисляването на се нарича извличане на корен -ти от число . Това е една от двете операции, обратни на степенуването,[11] а именно – намирането на основата на степента по даден показател и резултата от степенуването . Втората операция, логаритмуването, намира показателя на степента по известна основа и резултат.
Корени от реални числа
[редактиране | редактиране на кода]Корен -ти от реално число , в зависимост от четността и знака на , може да има от 0 до 2 реални стойности.
Общи свойства
[редактиране | редактиране на кода]- Нечетен корен от положително число – положително число, еднозначно определено.
| , където – нечетно |
- Например,
- Нечетен корен от отрицателно число – отрицателно число, еднозначно определено.
| , където – нечетно |
- Например,
- Четен корен от положително число има две стойности с противоположни знаци, но равни по модул.
| , където – четно |
- Например,
- Четен корен от отрицателно число не съществува в областта на реалните числа, тъй като при повдигането на кое да е реално число на степен с четен показател, резултатът ще бъде неотрицателно число. По-долу е показано как се намират такива корени от по-широката област на комплексните числа.
| не съществува, ако – четно |
- Какъвто и да е корен от нула е равен на нула.
| където |
Алгебрични свойства
[редактиране | редактиране на кода]- Взаимно съкращаване на корен и степен – за нечетни : , за четни :
- Ако , то и
Корен от произведение е равен на произведението на корените от множителите му:
Аналогично за деление:
Следващото равенство определя повдигането в дробна степен:
Стойността на корена не се изменя, ако показателят му и степента на коренувания израз се разделят на едно и също число:
- Пример:
За нечетните корени може да се изведе допълнително свойство:
Опростен вид на коренния израз
[редактиране | редактиране на кода]Коренният израз е в опростен вид, ако:[12]
- Няма множител пред подкоренния израз, който може да бъде записан като степен, по-голяма или равна на показателя на корена.
- Няма дроби под знака на корена.
- Няма корен в знаменател.
Например, за да се запише коренният израз в опростен вид, могат да се следват няколко стъпки. Първо се гледа под радикала за множител, който е идеален квадрат и се коренува:
След това трябва да се премахне дробта под радикала, който се заменя с дроб от радикали:
Накрая се премахва радикала от знаменателя, като се рационализира знаменателя:
Когато има корен в знаменател, винаги е възможно да се намери множител, с който да се умножат числителя и знаменателя, за да се опрости израза.[13][14] Например при факторизацията на сумата на два кубични корена:
Опростяването на коренни изрази, включващи вложени радикали може да бъде много трудно. Например, не е очевидно, че
Горното равенство може да бъде изведено така:
Функция на корена
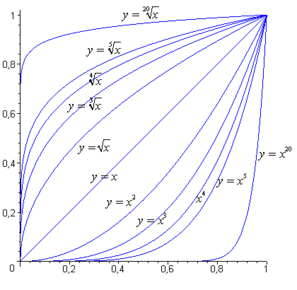
[редактиране | редактиране на кода]- Графики на функции на корена
- Функции на корена и обратните им степенни функции в интервала
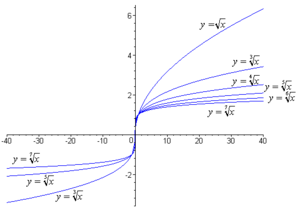
- Функции на корена:
— четни индекси 2, 4, 6
— нечетни индекси 3, 5, 7
Функцията на корена се отнася към алгебричните функции. Графиката на всяка функция на корена преминава през началото на координатната система и точката .
| Тип на функцията на корена | Област на определение |
|---|---|
| Четен индекс | |
| Нечетен индекс |
За всеки индекс коренната функция е строго нарастваща и непрекъсната навсякъде в областта си на определение. Тя е неограничено диференцируема навсякъде, освен в началните си координати, където производната се превръща в безкрайност.[15] Производната се определя по формулата:[16]
- . В частност, .
Функцията е неограничено интегрируема навсякъде в областта си на определение. Неопределеният интеграл се намира по формулата:
- . В частност, , където е произволна константа.
Съотношения на границите
[редактиране | редактиране на кода]Някои полезни съотношения на граници, съдържащи корени:[17]
Корени от комплексни числа
[редактиране | редактиране на кода]Пораждането на комплексните числа исторически е свързано с желанието за намирането на решение на квадратен корен от отрицателно число. Постепенно се изяснява, че комплексните числа притежават богати алгебрични и аналитични свойства – в частност, извличането на корен от тях винаги е възможно, макар и нееднозначно.
Способи за намиране
[редактиране | редактиране на кода]
Нека запишем комплексното число в тригонометричен вид:
- .
Тогава корен -ти от се определя от формулата на Моавър (в тригонометричен вид):[18]
или в експоненциална форма:
Корен -ти от ненулево комплексно число има решения, като всичките са различни.
Тъй като за всички решения на корена стойността на модула е еднаква, а се променя само неговият аргумент, всички решения на корена са разположени в комплексната равнина на окръжност с радиус с център в началото на координатната система. Корените разделят тази окръжност на равни части.
Примери
[редактиране | редактиране на кода]Да се намери . Тъй като по формулата се получава:
При се получава първия корен , а при се получава втория корен
Друг пример: да се намери . Подкоренният израз се представя в тригонометричен вид:
По формулата на Моавър се получава:
В резултат имемаме четири решения на корена:[19]
Може да се запише общ отговор във вида:
Комплексна функция на корена и Риманова повърхнина
[редактиране | редактиране на кода]Нека разгледаме комплексната функция на корен -ти: Според написаното по-горе, тази функция е многозначна (по-точно -значна) и това създава неудобства при изследването и приложението ѝ. В комплексния анализ вместо да се разглеждат многозначни функции в комплексна равнина, е взето друго решение – функцията да се разглежда като еднозначна, но определена не в равнината, а в по-сложно многообразие, наречено Риманова повърхнина.[20]


корен 4-ти
Римановата повърхнина на комплексната функция на корен -ти се състои от листа, свързани винтообразно, като последният лист е свързан с първия. Тази повърхност е непрекъсната и цялостна. Един от листовете съдържа главните решения на корена, получени като аналитично продължение на реалния корен от положителния лъч на реалната ос.
Единствената нула при функцията (от първи ред) се получава при . Особените точки са: и .
Източници
[редактиране | редактиране на кода]- ↑ Корень // Математическая энциклопедия (в 5 томах). Т. 3. Москва, Советская Энциклопедия, 1982.
- ↑ История математики, в трёх томах. Т. I. Москва, Наука. с. 42 – 46.
- ↑ История математики, в трёх томах. Т. I. Москва, Наука. с. 47.
- ↑ История математики, в трёх томах. Т. I. Москва, Наука. с. 169 – 171.
- ↑ Башмакова И. Г. Становление алгебры (из истории математических идей). Москва, Знание, 1979. с. 23.
- ↑ История математики, в трёх томах. Т. I. Москва, Наука. с. 275 – 276.
- ↑ История математики, в трёх томах. Т. I. Москва, Наука. с. 296 – 298.
- ↑ История математики, в трёх томах. Т. III. Москва, Наука. с. 56 – 59.
- ↑ История математики, в трёх томах. Т. III. Москва, Наука. с. 62.
- ↑ М. И. Сканави М. И. Элементарная математика. П. 1.11. С. 49.
- ↑ М. Я. Выгодский. Справочник по элементарной математике. 25. Москва, Наука, 1978. ISBN 5-17-009554-6.
- ↑ McKeague, Charles P. Elementary algebra. 2011. с. 470.
- ↑ B.F. Caviness, R.J. Fateman, „Simplification of Radical Expressions“, Proceedings of the 1976 ACM Symposium on Symbolic and Algebraic Computation, p. 329.
- ↑ Richard Zippel, „Simplification of Expressions Involving Radicals“, Journal of Symbolic Computation 1:189 – 210 (1985) DOI:10.1016/S0747-7171(85)80014-6
- ↑ Г. М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Т. I. 1966. с. 194 – 198.
- ↑ Г. М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Т. I. 1966. с. 215.
- ↑ Г. М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Т. I. 1966. с. 67, 131 – 132, 164, 166 – 167.
- ↑ Г. Корн, Т. Корн. Справочник по математике. 1973. с. 36 – 37.
- ↑ В. В. Зайцев, В. В. Рыжков, М. И. Сканави. Элементарная математика. Повторительный курс. 3. Москва, Наука, 1976. с. 68.
- ↑ А. Г. Свешников, А. Н. Тихонов. Теория функций комплексной переменной. 1967. с. 96 – 99, 28 – 29.
| Тази страница частично или изцяло представлява превод на страницата „Корень (математика)“ и страницата nth root в Уикипедия на руски и английски език. Оригиналните текстове, както и този превод, са защитени от Лиценза „Криейтив Комънс – Признание – Споделяне на споделеното“, а за творби, създадени преди юни 2009 година – от Лиценза за свободна документация на ГНУ. Прегледайте историята на редакциите на оригиналните страници тук и тук, за да видите списъка на техните съавтори. ВАЖНО: Този шаблон се отнася единствено до авторските права върху съдържанието на статията. Добавянето му не отменя изискването да се посочват конкретни източници на твърденията, които да бъдат благонадеждни. |


 French
French Deutsch
Deutsch

![{\displaystyle b={\sqrt[{n}]{a}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faa9d021810625038d355d8d04e49225a5f25121)

![{\displaystyle {\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7873203eb76042fcd24056c553de8c86054a2df)

![{\displaystyle \,{\sqrt[{n}]{x}}\,=\,x^{\frac {1}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ff3bb3595e08a8902ac2b0474837a531bd6c3b9)


![{\displaystyle {\sqrt[{3}]{\frac {8}{27}}}={\frac {2}{3}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6bdc22590a600d2eedc6841477696f1ae07ed9a)


















![{\displaystyle {\sqrt[{n}]{a}}=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a689688935f6bb305cb30a3f4d178cc01d49bb9)

![{\displaystyle {\sqrt[{3}]{125}}=5,\ {\sqrt[{5}]{32}}=2,\ {\sqrt[{15}]{1}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f472c8c6ad0d90dd45000ab47233f55ef5cbe42d)

![{\displaystyle {\sqrt[{3}]{-8}}=-2,\ {\sqrt[{5}]{-243}}=-3,\ {\sqrt[{7}]{-1}}=-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e37b2821a200bbf758c4661d5b13ee407a3d2f9)
![{\displaystyle {\sqrt[{n}]{a}}=\pm b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf21563d513e7b8292a2e4eea8618aa3bbfcfbc9)
![{\displaystyle {\sqrt {4}}=\pm 2,\ \ {\sqrt[{4}]{81}}=\pm 3,\ \ {\sqrt[{10}]{1024}}=\pm 2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d8feb54f099cefffd682affe2e09ff8fb84460)

![{\displaystyle {\sqrt[{n}]{0}}=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c650afa98b96756d746750fcaac8f71275a749a5)

![{\displaystyle {\sqrt[{n}]{a^{n}}}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bac4d6692e40c78859274a2b5c34e8cc8f5d3bc6)
![{\displaystyle {\sqrt[{n}]{a^{n}}}=|a|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8559b1369438746a6e523d299298caec78d606f9)

![{\displaystyle {\sqrt[{n}]{a}}<{\sqrt[{n}]{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34a6d3e9927917b69f4cc7627f60486addc2752c)
![{\displaystyle {\sqrt[{n}]{a}}b={\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/860cc0186083448f478e80763dceb36af0c42632)
![{\displaystyle {\sqrt[{n}]{\frac {a}{b}}}={\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}},\;b\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1adb683347197429f9209d6892c1e73de28eb6d4)
![{\displaystyle a^{m/n}={\sqrt[{n}]{a^{m}}}=\left({\sqrt[{n}]{a}}\right)^{m}=\left(a^{1/n}\right)^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c04c38a39ba30bd6185b8e80149e193635571fb3)
![{\displaystyle {\sqrt[{nk}]{a^{mk}}}={\sqrt[{n}]{a^{m}}},\;n,k\in \mathbb {N} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0903d86fa92aaf80561aaf7c181771501fd1d01)
![{\displaystyle {\sqrt[{6}]{64}}={\sqrt[{2\cdot 3}]{4^{3}}}={\sqrt {4}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9235ffd7400fbf03984e054403df9514d791bce)
![{\displaystyle {\sqrt[{n}]{\sqrt[{k}]{a}}}={\sqrt[{nk}]{a}},\;n,k\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4924a8105fb375c51d6ea91de74d04c6b759147c)
![{\displaystyle {\sqrt[{n}]{-a}}=-{\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f844766ed3a3b580508668e627e0bccb28f3faa)




![{\displaystyle {\frac {1}{{\sqrt[{3}]{a}}+{\sqrt[{3}]{b}}}}={\frac {{\sqrt[{3}]{a^{2}}}-{\sqrt[{3}]{ab}}+{\sqrt[{3}]{b^{2}}}}{\left({\sqrt[{3}]{a}}+{\sqrt[{3}]{b}}\right)\left({\sqrt[{3}]{a^{2}}}-{\sqrt[{3}]{ab}}+{\sqrt[{3}]{b^{2}}}\right)}}={\frac {{\sqrt[{3}]{a^{2}}}-{\sqrt[{3}]{ab}}+{\sqrt[{3}]{b^{2}}}}{a+b}}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc0dac1635353e53de31e40f49dd470d1deb220a)


![{\displaystyle [0;\ 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bd9d07c3fa150a68ff70c59f5360476fd970cdc)



![{\displaystyle {\frac {d}{dx}}{\sqrt[{n}]{x}}={\frac {1}{n{\sqrt[{n}]{x^{n-1}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cc55cd5fb693a81abf8db7397751adb98e61ada)

![{\displaystyle \int {\sqrt[{n}]{x}}\;dx={\frac {\sqrt[{n}]{x^{n+1}}}{1+{\frac {1}{n}}}}+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7660278dbc7fb62945550218b8c93f2c9beca94)


![{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{n}}=\lim _{n\to \infty }{\sqrt[{n}]{\ln n}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f0e1e5e54014face5332313d4e1aefc3e6860fb)
![{\displaystyle \lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)=\ln x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83d95e2439ebe22e00bd6addcf35e3377c462c23)
![{\displaystyle \lim _{x\to 0}{\frac {{\sqrt[{n}]{(x+1)^{m}}}-1}{x}}={\frac {m}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d69c07700c69c3c6ea11288bea5bc3b878ae7fc)
![{\displaystyle \lim _{n\to \infty }\left({\frac {{\sqrt[{n}]{a}}+{\sqrt[{n}]{b}}}{2}}\right)^{n}={\sqrt {ab}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59682d9b7c62b477d266fd422777cc3a7235143f)


![{\displaystyle {\sqrt[{n}]{z}}={\sqrt[{n}]{r}}\left(\cos {\frac {\varphi +2\pi k}{n}}+i\sin {\frac {\varphi +2\pi k}{n}}\right),\;k=0,1,\dots ,n-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb9a693c2750920814b93e1b7b66e2335b4248b5)

![{\displaystyle {\sqrt[{n}]{z}}={\sqrt[{n}]{r}}e^{\left(i{\frac {\varphi +2\pi k}{n}}\right)},\;k=0,1,\dots ,n-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e60f19c733e97d8043e87f9f2c81f523d513824)
![{\displaystyle {\sqrt[{n}]{r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10eb7386bd8efe4c5b5beafe05848fbd923e1413)







![{\displaystyle {\sqrt[{4}]{-16}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b16dc4a185ac1049e43e6ad7372e8f9686312dc)

![{\displaystyle z_{k}={\sqrt[{4}]{-16}}={\sqrt[{4}]{16}}\left(\cos {\frac {\pi +2k\pi }{4}}+i\sin {\frac {\pi +2k\pi }{4}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b48ba51e9b2752410472bc400a9513268ba46aaf)




![{\displaystyle {\sqrt[{4}]{-16}}={\sqrt {2}}\ (\pm 1\pm i)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18ed9f08bb488165796d6d70fed26860f8d0b7b9)
![{\displaystyle w={\sqrt[{n}]{z}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe2a25829482fe1c9b8dd10f629067ba547992af)

