Poliedro romo , la enciclopedia libre

En geometría, un poliedro romo (traducción libre del término inglés snub, con el significado de "chato") es un poliedro obtenido al realizar una operación de achatado, que equivale a la alternación de un poliedro previamente omnitruncado o truncado, según la definición.^[1]​ Algunos autores, pero no todos, incluyen los antiprismas como poliedros romos, ya que se obtienen mediante esta construcción a partir de un poliedro degenerado con solo dos caras (un diedro).

Los poliedros romos quirales no siempre tienen simetría especular y, por lo tanto, a veces tienen dos formas enantiomorfas (levógiras y dextrógiras) que son especulares entre sí. Sus grupos de simetría son todos los grupos de puntos del espacio tridimensional.

Los poliedros romos tienen símbolo de Wythoff | p q r y por extensión, configuración de vértices 3.p.3.q.3.r. Los poliedros retrorromos (un subconjunto de los poliedros romos, que contiene al gran icosaedro, al pequeño icosicosidodecaedro retrorromo y al gran icosidodecaedro retrorromo) todavía tienen esta forma de símbolo de Wythoff, pero sus configuraciones de vértice son:^[1]​

${\displaystyle {\frac {(3.-p.3.-q.3.-r)}{2}}}$

Hay 12 poliedros romos uniformes, sin incluir los antiprismas, el icosaedro como un tetraedro romo, el gran icosaedro como un tetraedro retrorromo y el gran dirrombidodecaedro birromo, también conocido como figura de Skilling.

Cuando el triángulo de Schwarz del poliedro romo es isósceles, el poliedro romo no es quiral. Este es el caso de los antiprismas, el icosaedro, el gran icosaedro, el pequeño icosicosidodecaedro romo y el pequeño icosicosidodecaedro retrorromo.

En las siguientes imágenes de la generación de las figuras achatadas (que muestran un poliedro romo distorsionado, topológicamente idéntico a la versión uniforme, obtenido alternando geométricamente el poliedro omnitruncado uniforme principal), cuando el color verde no está presente, las caras generadas mediante la alternación están coloreadas de rojo y amarillo, mientras que los triángulos romos son azules. Cuando está presente el verde (solo para los casos del icosidodecadodecaedro romo y del gran dodecicosidodecaedro romo), las caras derivadas de la alternancia son rojas, amarillas y azules, mientras que los triángulos romos son verdes.

Poliedro romo	Imagen	Poliedro omnitruncado original	Imagen	Generación del achatado	Grupo de simetría	Símbolo de Wythoff Descripción de vértices
Icosaedro (tetraedro romo)		Octaedro truncado		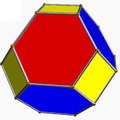	Ih (Th)	| 3 3 2 3.3.3.3.3
Gran icosaedro (tetraedro retrorromo)		Octaedro truncado			Ih (Th)	| 2 3/2 3/2 (3.3.3.3.3)/2
Cubo romo o cuboctaedro romo		Cuboctaedro truncado			O	| 4 3 2 3.3.3.3.4
Dodecaedro romo o icosidodecaedro romo		Icosidodecaedro truncado			I	| 5 3 2 3.3.3.3.5
Pequeño icosicosidodecaedro romo		Icosaedro truncado doblemente recubierto			Ih	| 3 3 5/2 3.3.3.3.3.5/2
Dodecadodecaedro romo		Pequeño rombidodecaedro con 12 caras extra ({10/2})		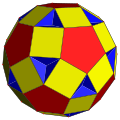	I	| 5 5/2 2 3.3.5/2.3.5
Icosidodecadodecaedro romo		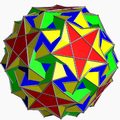Dodecadodecaedro icositruncado			I	| 5 3 5/3 3.5/3.3.3.3.5
Gran icosidodecaedro romo		Rombicosaedro con 12 caras extra ({10/2})			I	| 3 5/2 2 3.3.5/2.3.3
Dodecadodecaedro romo invertido		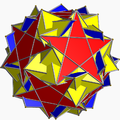Dodecadodecaedro truncado			I	| 5 2 5/3 3.5/3.3.3.3.5
Gran dodecicosidodecaedro romo		Gran dodecicosaedro con 12 caras extra ({10/2})		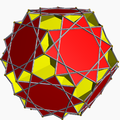—	I	| 3 5/2 5/3 3.5/3.3.5/2.3.3
Gran icosidodecaedro romo invertido		Gran icosidodecaedro truncado		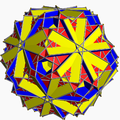	I	| 3 2 5/3 3.5/3.3.3.3
Pequeño icosicosidodecaedro retrorromo		Icosaedro truncado doblemente recubierto		—	Ih	| 5/2 3/2 3/2 (3.3.3.3.3.5/2)/2
Gran icosidodecaedro retrorromo		Gran rombidodecaedro con 20 caras extra ({6/2})		—	I	| 2 5/3 3/2 (3.3.3.5/2.3)/2
Gran dirrombicosidodecaedro		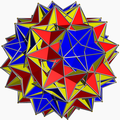—	—	—	Ih	| 3/2 5/3 3 5/2 (4.3/2.4.5/3.4.3.4.5/2)/2
Gran dirrombidodecaedro birromo		—	—	—	Ih	| (3/2) 5/3 (3) 5/2 (3/2.3/2.3/2.4.5/3.4.3.3.3.4.5/2.4)/2

Notas:

• Icosaedro, cubo romo y dodecaedro romo son los tres únicos poliedros romos convexos. Se obtienen mediante el achatado del octaedro truncado, del cuboctaedro truncado y del icosidodecaedro truncado; tres poliedros cuasirregulares truncados convexos.
• El único poliedro romo con el grupo de simetrías octaédrico quiral es el cubo romo.
• Solo el icosaedro y el gran icosaedro son también poliedros regulares. También son deltaedros.
• Solo el icosaedro, el gran icosaedro, el pequeño icosicosidodecaedro romo, el pequeño icosicosidodecaedro retrorromo, el gran dirrombicosidodecaedro y el gran dirrombidodecaedro birromo también poseen simetrías de reflexión.

También existe el conjunto infinito de antiprismas. Se forman a partir de prismas, que se truncan como hosoedros, poliedros regulares degenerados. A continuación se enumeran todos los tipos hasta la forma hexagonal. En las imágenes que muestran la generación del achatado, las caras derivadas de la alternancia (de las bases del prisma) están coloreadas en rojo y los triángulos romos están coloreados en amarillo. La excepción es el tetraedro, para el que todas las caras se generan como triángulos procedentes del achatado rojos, ya que alternar las bases cuadradas del cubo da como resultado dígonos degenerados como caras.

Poliedro romo	Imagen	Poliedro omnitruncado original	Imagen	Generación del achatado	Grupo de simetría	Símbolo de Wythoff Descripción de vértices
Tetraedro		Cubo			Td (D2d)	| 2 2 2 3.3.3
Octaedro		Prisma hexagonal			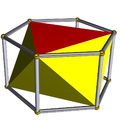Oh (D3d)	| 3 2 2 3.3.3.3
Antiprisma cuadrado		Prisma octogonal			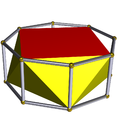D4d	| 4 2 2 3.4.3.3
Antiprisma pentagonal		Prisma decagonal			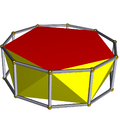D5d	| 5 2 2 3.5.3.3
Antiprisma pentagrámico		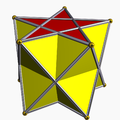Prisma pentagonal doblemente recubierto			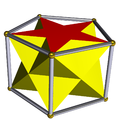D5h	| 5/2 2 2 3.5/2.3.3
Antiprisma cruzado pentagrámico		Prisma decagrámico			D5d	| 2 2 5/3 3.5/3.3.3
Antiprisma hexagonal		Prisma dodecagonal			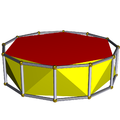D6d	| 6 2 2 3.6.3.3

Notas:

• Dos de estos poliedros pueden construirse a partir de los dos primeros poliedros romos de la lista que comienza con el icosaedro: el antiprisma pentagonal es un icosaedro parabidisminuido y el antiprisma cruzado pentagrámico es un gran icosaedro parabidisminuido, también conocido como gran icosaedro parabireplenado.

Dos sólidos de Johnson son poliedros romos: el biesfenoide romo y el antiprisma cuadrado romo. Ninguno de ellos es quiral.

Poliedro romo	Imagen	Poliedro original	Imagen	Grupo de simetría
Biesfenoide romo		Disfenoide		D2d
Antiprisma cuadrado romo		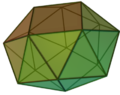Antiprisma cuadrado		D4d

• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), «Uniform polyhedra», Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 246 (916): 401-450, ISSN 0080-4614, JSTOR 91532, MR 0062446, S2CID 202575183, doi:10.1098/rsta.1954.0003 .
• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. 
• Skilling, J. (1975), «The complete set of uniform polyhedra», Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 278 (1278): 111-135, ISSN 0080-4614, JSTOR 74475, MR 0365333, S2CID 122634260, doi:10.1098/rsta.1975.0022 .
• Mäder, R. E. Poliedros uniformes. Mathematica J. 3, 48-57, 1993.

Operadores de poliedros

Semilla	Truncamiento	Rectificación	Bitruncamiento	Dual	Expansión	Omnitruncamiento	Alternaciones
t0{p,q} {p,q}	t01{p,q} t{p,q}	t1{p,q} r{p,q}	t12{p,q} 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q} rr{p,q}	t012{p,q} tr{p,q}	ht0{p,q} h{q,p}	ht12{p,q} s{q,p}	ht012{p,q} sr{p,q}