برآوردگر بیشینه‌گر احتمال پسین - ویکی‌پدیا، دانشنامهٔ آزاد

در آمار، برآوردگر بیشینه‌گر احتمال پسین (به انگلیسی: Maximum a posteriori estimation) یک پارامتر، مد توزیع احتمال پسین آن پارامتر است. به بیان ریاضی، اگر داده ${\displaystyle X}$ بر اساس توزیع ${\displaystyle f(X|\theta )}$ با پارامتر ${\displaystyle \theta }$ توزیع شده‌باشند و ${\displaystyle g(\theta )}$ و ${\displaystyle f(X|\theta )}$ به ترتیب احتمال پیشین پارامتر و درستنمایی داده را نشان دهند، برآوردگر بیشینه‌گر احتمال پسین برابر خواهد بود با:

${\displaystyle {\hat {\theta }}_{\mathrm {MAP} }(x)={\underset {\theta }{\operatorname {arg\,max} }}\ {\frac {f(x|\theta )\,g(\theta )}{\displaystyle \int _{\vartheta }f(x|\vartheta )\,g(\vartheta )\,d\vartheta }}={\underset {\theta }{\operatorname {arg\,max} }}\ f(x|\theta )\,g(\theta ).\!}$

برآوردگر بیشینه‌گر احتمال پسین ارتباط نزدیکی با برآورد درستنمایی بیشینه دارد، با این تفاوت که برای پارامتر مورد تخمین احتمال پیشین را هم در نظر می‌گیرد. در نتیجه، می‌توان برآوردگر بیشینه‌گر احتمال پسین را همان برآورد درست‌نمایی بیشینه دانست به همراه یک تنظیم‌گر.

فرض کنید میخواهیم پارامتر جمعیت مشاهده نشده‌ی ${\displaystyle \theta }$ را بر اساس مشاهدات ${\displaystyle x}$ تخمین بزنیم. فرض کنید ${\displaystyle f}$ توزیع نمونه گیری ${\displaystyle x}$ باشد، پس احتمال ${\displaystyle x}$ وقتی که پارامتر جمعیت ${\displaystyle \theta }$ باشد، ${\displaystyle f(x|\theta )}$ است. تابع زیر به تابع درست‌نمایی معروف است:

${\displaystyle \theta \mapsto f(x|\theta )}$

و تخمین زیر، برآورد حداکثر درست نمایی است:

${\displaystyle {\hat {\theta }}_{\mathrm {MLE} }(x)={\underset {\theta }{\operatorname {arg\,max} }}\ f(x\mid \theta )}$

حال فرض کنید توزیع پیشین ${\displaystyle g}$ روی ${\displaystyle \theta }$ وجود داشته باشد. این کار به ما اجازه می دهد تا با ${\displaystyle \theta }$ به عنوان یک متغیر تصادفی رفتار کنیم. محاسبه‌ی توزیع پسین ${\displaystyle \theta }$ با استفاده از قانون بیز به صورت زیر است:

${\displaystyle \theta \mapsto f(\theta \mid x)={\frac {f(x\mid \theta )\,g(\theta )}{\displaystyle \int _{\Theta }f(x\mid \vartheta )\,g(\vartheta )\,d\vartheta }}}$

${\displaystyle g}$ تابع چگالی ${\displaystyle \theta }$ و ${\displaystyle \Theta }$ دامنه‌ی ${\displaystyle g}$ است.

روش برآوردگر بیشینه‌گر احتمال پسین به صورت زیر است:

${\displaystyle {\hat {\theta }}_{\mathrm {MAP} }(x)={\underset {\theta }{\operatorname {arg\,max} }}\ f(\theta \mid x)={\underset {\theta }{\operatorname {arg\,max} }}\ {\frac {f(x\mid \theta )\,g(\theta )}{\displaystyle \int _{\Theta }f(x\mid \vartheta )\,g(\vartheta )\,d\vartheta }}={\underset {\theta }{\operatorname {arg\,max} }}\ f(x\mid \theta )\,g(\theta ).}$

مخرج کسر بالا همواره مثبت است و نیز وابسته به ${\displaystyle \theta }$ نیست، در نتیجه نقشی در بهینه سازی تابع ندارد. وقتی ${\displaystyle g}$ تابعی ثابت باشد آن گاه برآوردگر بیشینه‌گر احتمال پسین همانند برآوردگر بیشینه درست نمایی عمل میکند.

هر وقت تابع هزینه به شکل زیر باشد:

${\displaystyle L(\theta ,a)={\begin{cases}0,&{\text{if }}|a-\theta |<c,\\1,&{\text{otherwise}},\\\end{cases}}}$

و ${\displaystyle c}$ به عدد 0 نزدیک شود، برآوردگر بیزی به برآوردگر بیشینه‌گر احتمال پسین نزدیکتر میشود(با فرض اینکه توزیع ${\displaystyle \theta }$ شبه مقعر باشد). ولی به صورت کلی برآوردگر بیشینه‌گر احتمال پسین یک برآوردگر بیزی نیست مگر آنکه ${\displaystyle \theta }$ گسسته باشد.

محاسبه:

برآوردگر بیشینه‌گر احتمال پسین به چندین روش می‌تواند محاسبه شود:

1. تحلیلی، زمانی که مد(های) توزیع پسین به شکل عبارت فرم بسته باشد. این مورد زمانی است که توزیع مزدوج پیشین استفاده میشود.
2. به وسیله‌ی بهینه سازی عددی، مانند روش گرادیان مزدوج یا روش نیوتون. این روش معمولا نیازمند مشتقات اول و دوم است.
3. به وسیله تغییر دادن الگوریتم امید ریاضی بیشینه کردن. در این روش نیازی به محاسبه مشتقات چگالی پسین نیست.
4. به روش مونت‌کارلو و با استفاده از الگوریتم تبرید شبیه‌سازی‌شده.

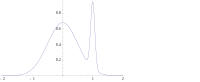
در حالی که فقط شرایط خفیف برای برآوردگر بیشینه‌گر احتمال پسین نیاز است تا نمونه‌ی حدی یک تخمین‌گر بیزی باشد(تحت تابع هزینه‌ی 1-0)، ولی عموما نمایانگر روش‌های بیزی نیست. آن به این دلیل است که برآوردگرهای بیشینه‌گر احتمال پسین، تخمین‌گر نقطه هستند در حالی که روش‌های بیزی از توزیع‌ها برای خلاصه‌سازی داده و نتیجه‌گیری استفاده می‌کنند. از این رو روش‌های بیزی برای گزارش پسین میانگین یا میانه(در کنار بازه‌های مورد قبول) معتبر هستند، زیرا این تخمین‌گرها به‌ترتیب تحت خطای مربعات و خطای خطی بهینه هستند و همچنین توزیع پسین ممکن است توزیع آنالیزی ساده‌ای نداشته باشد(در چنین شرایطی توزیع با استفاده از زنجیره مارکوف مونت‌کارلو می‌تواند شبیه‌سازی شود در حالی که بهینه‌سازی برای پیدا کردن مدهایش ممکن است سخت یا ناممکن باشد).

در بسیاری از انواع مدل‌ها همانند مدل‌های مخلوط، پسین ممکن است چند-مُدال باشد. در این شرایط توصیه آن است که بیشترین مد انتخاب شود که همواره امکان پذیر نیست و گاهی احتمال دارد ناممکن باشد. علاوه‌بر این‌ها بیشترین مد ممکن است بیانگر ویژگی‌های اغلب پسین‌ها نباشد.

برخلاف برآوردگرهای درست‌نمایی بیشینه، برآوردگرهای بیشینه‌گر احتمال پسین هنگام دوباره‌سازی پارامترها ثابت نیستند. زیرا تغییر از یکی به دیگری ژاکوبین جدیدی را ایجاد می‌کند که روی مکان بیشینه اثر می‌گذارد.

فرض کنید می‌خواهیم ورودی‌های ${\displaystyle x}$را مثبت یا منفی طبقه‌بندی کنیم. سه فرضیه ممکن ${\displaystyle h_{1}}$،${\displaystyle h_{2}}$و ${\displaystyle h_{3}}$ درباره‌ی روش صحیح دسته‌بندی به ترتیب با پسین‌های 0.4، 0.3 و 0.3 وجود دارد. فرض کنید برای نمونه‌ی جدید ${\displaystyle x}$، سه دسته‌بندی کننده‌ی ذکر شده به‌ترتیب ${\displaystyle x}$را مثبت، منفی و منفی دسته‌بندی می‌کند. ${\displaystyle x}$ با استفاده از برآوردگر بیشینه‌گر احتمال پسین برای دسته‌بندی کننده‌ی ${\displaystyle h_{1}}$ مثبت و با استفاده از تخمین‌گر بیزی روی همه‌ی فرضیه‌ها، منفی دسته‌بندی می‌شود.

فرض کنید ${\displaystyle (x_{1},x_{2},...,x_{n})}$ دنباله ای از متغیرهای تصادفی مستقل با توزیع یکسان ${\displaystyle N(\mu ,\sigma _{v}^{2})}$ و ${\displaystyle N(\mu _{0},\sigma _{m}^{2})}$ توزیع پسین ${\displaystyle \mu }$ باشد. میخواهیم برآوردگر بیشینه‌گر احتمال پسین ${\displaystyle \mu }$ را پیدا کنیم.

تابعی که میخواهیم بیشینه کنیم به صورت زیر است:

${\displaystyle f(\mu )f(x\mid \mu )=\pi (\mu )L(\mu )={\frac {1}{{\sqrt {2\pi }}\sigma _{m}}}\exp \left(-{\frac {1}{2}}\left({\frac {\mu -\mu _{0}}{\sigma _{m}}}\right)^{2}\right)\prod _{j=1}^{n}{\frac {1}{{\sqrt {2\pi }}\sigma _{v}}}\exp \left(-{\frac {1}{2}}\left({\frac {x_{j}-\mu }{\sigma _{v}}}\right)^{2}\right)}$

که هم ارز است با کمینه کردن تابع زیر از ${\displaystyle \mu }$:

${\displaystyle \sum _{j=1}^{n}\left({\frac {x_{j}-\mu }{\sigma _{v}}}\right)^{2}+\left({\frac {\mu -\mu _{0}}{\sigma _{m}}}\right)^{2}.}$

در نهایت برآوردگر بیشینه‌گر احتمال پسین برای ${\displaystyle \mu }$ به شکل زیر در می‌آید:

${\displaystyle {\hat {\mu }}_{\mathrm {MAP} }={\frac {\sigma _{m}^{2}\,n}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}\left({\frac {1}{n}}\sum _{j=1}^{n}x_{j}\right)+{\frac {\sigma _{v}^{2}}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}\,\mu _{0}={\frac {\sigma _{m}^{2}\left(\sum _{j=1}^{n}x_{j}\right)+\sigma _{v}^{2}\,\mu _{0}}{\sigma _{m}^{2}\,n+\sigma _{v}^{2}}}}$

که یک رابطه‌ی خطی وزن دار بین میانگین پیشین و میانگین نمونه است.

وقتی ${\displaystyle \sigma _{m}}$ به بینهایت میل کند اصطلاحا به این، پیشین غیر آموزنده گفته میشود. در این حالت ${\displaystyle {\hat {\mu }}_{\mathrm {MAP} }\to {\hat {\mu }}_{\mathrm {ML} }}$.