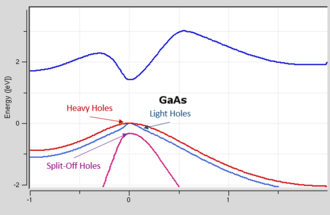
ساختار نواری GaitAs در مدل تنگبست، که حفرههای سنگین، سوراخهای سبک و سوراخهای تقسیمشده را نشان میدهد. در فیزیک حالت جامد ، مدل تنگبست (یا تقریب بستگی قوی ) رویکردی برای محاسبه ساختار نواری با استفاده از تقریب برهمنهی توابع موج اتمهای منزوی در ساختار بلوری است. این مدل مشابه روش ترکیب خطی اوربیتالهای اتمی است که در شیمی کاربرد دارد. مدل تنگبست برای طیف گستردهای از جامدات استفاده می شود. این مدل در بسیاری از موارد نتایج کیفی خوبی به همراه دارد و میتواند با مدلهای دیگری ترکیب شود. اگرچه مدل تنگبست یک مدل تکالکترونی است، اما این مدل همچنین مبنایی برای محاسبات پیشرفتهتر مانند محاسبه حالتهای سطح و انواع مختلفی از سیستم چندپیکره و محاسبات شبه ذرات را فراهم میکند.[ ۱] [ ۲]
نام «تنگبست» در این نظریه نواری نشان دهنده بستگی قوی بین الکترونهای این مدل مکانیک کوانتومی در جامدات است. الکترونها در این مدل بسیار مقید به اتمی که به آن تعلق دارند میباشند و برهمکنش محدودی با حالتها و پتانسیلهای اتمهای جامد دارند. در نتیجه، تابع موج الکترون تقریباً شبیه اوربیتال اتمی اتم آزادی خواهد بود که به آن تعلق دارد. انرژی الکترون نیز بسیار نزدیک به انرژی یونش الکترون در اتم یا یون آزاد خواهد بود زیرا برهمکنش با پتانسیل اتمهای مجاور محدود است.
اگرچه فرمول ریاضی هامیلتونین مدل تنگبست[ ۳] شیمیدانها به سادگی انرژی پیوند نامیده می شود.
اوربیتالهای اتمی با φ m ( r ) {\displaystyle \varphi _{m}(\mathbf {r} )} توابع ویژه هامیلتونی H a t {\displaystyle H_{\rm {at}}} بلور قرار می گیرد، این تابع موج اتمی با اتمهای مجاور همپوشانی دارد، و بنابراین، توابع ویژه هامیلتونی بلور واقعی نیستند. زمانی که الکترونها به هم متصل میشوند، همپوشانی کمتر میشود، که نشان دهندهی «پیوند قوی» است. هرگونه اصلاح در پتانسیل اتمی Δ U {\displaystyle \Delta U} H {\displaystyle H}
H ( r ) = H a t ( r ) + ∑ R n ≠ 0 V ( r − R n ) = H a t ( r ) + Δ U ( r ) {\displaystyle H(\mathbf {r} )=H_{\mathrm {at} }(\mathbf {r} )+\sum _{\mathbf {R} _{n}\neq \mathbf {0} }V(\mathbf {r} -\mathbf {R} _{n})=H_{\mathrm {at} }(\mathbf {r} )+\Delta U(\mathbf {r} )\!} V ( r − R n ) {\displaystyle V(\mathbf {r} -\mathbf {R} _{n})} R n {\displaystyle \mathbf {R} _{n}} شبکه کریستالی است. ψ m {\displaystyle \psi _{m}} معادله شرودینگر تک الکترونی مستقل از زمان است که به صورت ترکیب خطی از اوربیتالهای اتمی تقریب زده میشود:
ψ m ( r ) = ∑ R n b m ( R n ) φ m ( r − R n ) {\displaystyle \psi _{m}(\mathbf {r} )=\sum _{\mathbf {R} _{n}}b_{m}(\mathbf {R} _{n})\ \varphi _{m}(\mathbf {r} -\mathbf {R} _{n})} که m {\displaystyle m}
[ ویرایش ] قضیه بلوخ بیان میکند که تابع موج در یک کریستال میتواند تحت انتقال تنها با یک عامل فاز تغییر کند:
ψ ( r + R ℓ ) = e i k ⋅ R ℓ ψ ( r ) {\displaystyle \psi (\mathbf {r+R_{\ell }} )=e^{i\mathbf {k\cdot R_{\ell }} }\psi (\mathbf {r} )\,}
که k {\displaystyle \mathbf {k} } بردار موج تابع موج است. در نتیجه،
∑ R n b m ( R n ) φ m ( r − R n + R ℓ ) = e i k ⋅ R ℓ ∑ R n b m ( R n ) φ m ( r − R n ) {\displaystyle \sum _{\mathbf {R} _{n}}b_{m}(\mathbf {R} _{n})\ \varphi _{m}(\mathbf {r} -\mathbf {R} _{n}+\mathbf {R} _{\ell })=e^{i\mathbf {k} \cdot \mathbf {R} _{\ell }}\sum _{\mathbf {R} _{n}}b_{m}(\mathbf {R} _{n})\ \varphi _{m}(\mathbf {r} -\mathbf {R} _{n})\ } با تعویض R p = R n − R ℓ {\displaystyle \mathbf {R} _{p}=\mathbf {R} _{n}-\mathbf {R_{\ell }} }
b m ( R p + R ℓ ) = e i k ⋅ R ℓ b m ( R p ) {\displaystyle b_{m}(\mathbf {R} _{p}+\mathbf {R} _{\ell })=e^{i\mathbf {k\cdot R_{\ell }} }b_{m}(\mathbf {R} _{p})\,}
یا
b m ( R ℓ ) = e i k ⋅ R ℓ b m ( 0 ) . {\displaystyle b_{m}(\mathbf {R} _{\ell })=e^{i\mathbf {k} \cdot \mathbf {R} _{\ell }}b_{m}(\mathbf {0} )\ .}
نرمالسازی تابع موج به واحد:
∫ d 3 r ψ m ∗ ( r ) ψ m ( r ) = 1 {\displaystyle \int d^{3}r\ \psi _{m}^{*}(\mathbf {r} )\psi _{m}(\mathbf {r} )=1} = ∑ R n b m ∗ ( R n ) ∑ R ℓ b m ( R ℓ ) ∫ d 3 r φ m ∗ ( r − R n ) φ m ( r − R ℓ ) {\displaystyle =\sum _{\mathbf {R} _{n}}b_{m}^{*}(\mathbf {R} _{n})\sum _{\mathbf {R_{\ell }} }b_{m}(\mathbf {R_{\ell }} )\int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} -\mathbf {R} _{n})\varphi _{m}(\mathbf {r} -\mathbf {R} _{\ell })} = b m ∗ ( 0 ) b m ( 0 ) ∑ R n e − i k ⋅ R n ∑ R ℓ e i k ⋅ R ℓ ∫ d 3 r φ m ∗ ( r − R n ) φ m ( r − R ℓ ) {\displaystyle =b_{m}^{*}(0)b_{m}(0)\sum _{\mathbf {R} _{n}}e^{-i\mathbf {k\cdot R_{n}} }\sum _{\mathbf {R_{\ell }} }e^{i\mathbf {k\cdot R_{\ell }} }\ \int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} -\mathbf {R} _{n})\varphi _{m}(\mathbf {r} -\mathbf {R} _{\ell })} = N b m ∗ ( 0 ) b m ( 0 ) ∑ R p e − i k ⋅ R p ∫ d 3 r φ m ∗ ( r − R p ) φ m ( r ) {\displaystyle =Nb_{m}^{*}(0)b_{m}(0)\sum _{\mathbf {R} _{p}}e^{-i\mathbf {k} \cdot \mathbf {R} _{p}}\ \int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} -\mathbf {R} _{p})\varphi _{m}(\mathbf {r} )\ } = N b m ∗ ( 0 ) b m ( 0 ) ∑ R p e i k ⋅ R p ∫ d 3 r φ m ∗ ( r ) φ m ( r − R p ) , {\displaystyle =Nb_{m}^{*}(0)b_{m}(0)\sum _{\mathbf {R} _{p}}e^{i\mathbf {k} \cdot \mathbf {R} _{p}}\ \int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} )\varphi _{m}(\mathbf {r} -\mathbf {R} _{p})\ ,} بنابراین نرمالسازی نتیجه میدهد:
b m ∗ ( 0 ) b m ( 0 ) = 1 N ⋅ 1 1 + ∑ R p ≠ 0 e i k ⋅ R p α m ( R p ) {\displaystyle b_{m}^{*}(0)b_{m}(0)={\frac {1}{N}}\ \cdot \ {\frac {1}{1+\sum _{\mathbf {R} _{p}\neq 0}e^{i\mathbf {k} \cdot \mathbf {R} _{p}}\alpha _{m}(\mathbf {R} _{p})}}\,} که α m ( R p ) {\textstyle \alpha _{m}(\mathbf {R} _{p})}
b m ( 0 ) ≈ 1 N {\displaystyle b_{m}(0)\approx {\frac {1}{\sqrt {N}}}\,} و
ψ m ( r ) ≈ 1 N ∑ R n e i k ⋅ R n φ m ( r − R n ) . {\displaystyle \psi _{m}(\mathbf {r} )\approx {\frac {1}{\sqrt {N}}}\sum _{\mathbf {R} _{n}}e^{i\mathbf {k} \cdot \mathbf {R} _{n}}\ \varphi _{m}(\mathbf {r} -\mathbf {R} _{n})\ .}
با استفاده از شکل همبستگی قوی برای توابع موج، و با فرض اینکه فقط سطح انرژی اتم m در نوار انرژی mام مهم است، انرژی بلوخ ε m {\displaystyle \varepsilon _{m}}
ε m = ∫ d 3 r ψ m ∗ ( r ) H ( r ) ψ m ( r ) {\displaystyle \varepsilon _{m}=\int d^{3}r\ \psi _{m}^{*}(\mathbf {r} )H(\mathbf {r} )\psi _{m}(\mathbf {r} )} = ∑ R n b m ∗ ( R n ) ∫ d 3 r φ m ∗ ( r − R n ) H ( r ) ψ m ( r ) {\displaystyle =\sum _{\mathbf {R} _{n}}b_{m}^{*}(\mathbf {R} _{n})\ \int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} -\mathbf {R} _{n})H(\mathbf {r} )\psi _{m}(\mathbf {r} )} = ∑ R n b m ∗ ( R n ) ∫ d 3 r φ m ∗ ( r − R n ) H a t ( r ) ψ m ( r ) + ∑ R n b m ∗ ( R n ) ∫ d 3 r φ m ∗ ( r − R n ) Δ U ( r ) ψ m ( r ) {\displaystyle =\sum _{\mathbf {R} _{n}}b_{m}^{*}(\mathbf {R} _{n})\ \int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} -\mathbf {R} _{n})H_{\mathrm {at} }(\mathbf {r} )\psi _{m}(\mathbf {r} )+\sum _{\mathbf {R} _{n}}b_{m}^{*}(\mathbf {R} _{n})\ \int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} -\mathbf {R} _{n})\Delta U(\mathbf {r} )\psi _{m}(\mathbf {r} )} = ∑ R n , R l b m ∗ ( R n ) b m ( R l ) ∫ d 3 r φ m ∗ ( r − R n ) H a t ( r ) φ m ( r − R l ) + b m ∗ ( 0 ) ∑ R n e − i k ⋅ R n ∫ d 3 r φ m ∗ ( r − R n ) Δ U ( r ) ψ m ( r ) {\displaystyle =\sum _{\mathbf {R} _{n},\mathbf {R} _{l}}b_{m}^{*}(\mathbf {R} _{n})b_{m}(\mathbf {R} _{l})\ \int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} -\mathbf {R} _{n})H_{\mathrm {at} }(\mathbf {r} )\varphi _{m}(\mathbf {r} -\mathbf {R} _{l})+b_{m}^{*}(0)\sum _{\mathbf {R} _{n}}e^{-i\mathbf {k} \cdot \mathbf {R} _{n}}\ \int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} -\mathbf {R} _{n})\Delta U(\mathbf {r} )\psi _{m}(\mathbf {r} )} = b m ∗ ( 0 ) b m ( 0 ) N ∫ d 3 r φ m ∗ ( r ) H a t ( r ) φ m ( r ) + b m ∗ ( 0 ) ∑ R n e − i k ⋅ R n ∫ d 3 r φ m ∗ ( r − R n ) Δ U ( r ) ψ m ( r ) {\displaystyle =b_{m}^{*}(\mathbf {0} )b_{m}(\mathbf {0} )\ N\int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} )H_{\mathrm {at} }(\mathbf {r} )\varphi _{m}(\mathbf {r} )+b_{m}^{*}(0)\sum _{\mathbf {R} _{n}}e^{-i\mathbf {k} \cdot \mathbf {R} _{n}}\ \int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} -\mathbf {R} _{n})\Delta U(\mathbf {r} )\psi _{m}(\mathbf {r} )} ≈ E m + b m ∗ ( 0 ) ∑ R n e − i k ⋅ R n ∫ d 3 r φ m ∗ ( r − R n ) Δ U ( r ) ψ m ( r ) . {\displaystyle \approx E_{m}+b_{m}^{*}(0)\sum _{\mathbf {R} _{n}}e^{-i\mathbf {k} \cdot \mathbf {R} _{n}}\ \int d^{3}r\ \varphi _{m}^{*}(\mathbf {r} -\mathbf {R} _{n})\Delta U(\mathbf {r} )\psi _{m}(\mathbf {r} )\ .} در آخرین مرحله انتگرال همپوشانی صفر فرض شده و بنابراین b m ∗ ( 0 ) b m ( 0 ) = 1 N {\displaystyle b_{m}^{*}(\mathbf {0} )b_{m}(\mathbf {0} )={\frac {1}{N}}}
ε m ( k ) = E m − N | b m ( 0 ) | 2 ( β m + ∑ R n ≠ 0 ∑ l γ m , l ( R n ) e i k ⋅ R n ) , {\displaystyle \varepsilon _{m}(\mathbf {k} )=E_{m}-N\ |b_{m}(0)|^{2}\left(\beta _{m}+\sum _{\mathbf {R} _{n}\neq 0}\sum _{l}\gamma _{m,l}(\mathbf {R} _{n})e^{i\mathbf {k} \cdot \mathbf {R} _{n}}\right)\ ,} = E m − β m + ∑ R n ≠ 0 ∑ l e i k ⋅ R n γ m , l ( R n ) 1 + ∑ R n ≠ 0 ∑ l e i k ⋅ R n α m , l ( R n ) {\displaystyle =E_{m}-\ {\frac {\beta _{m}+\sum _{\mathbf {R} _{n}\neq 0}\sum _{l}e^{i\mathbf {k} \cdot \mathbf {R} _{n}}\gamma _{m,l}(\mathbf {R} _{n})}{\ \ 1+\sum _{\mathbf {R} _{n}\neq 0}\sum _{l}e^{i\mathbf {k} \cdot \mathbf {R} _{n}}\alpha _{m,l}(\mathbf {R} _{n})}}\,} که در آن E m {\textstyle E_{m}} m {\displaystyle m} α m , l {\displaystyle \alpha _{m,l}} β m {\displaystyle \beta _{m}} γ m , l {\displaystyle \gamma _{m,l}}
↑ کیتل، چارلز. Introduction to Solid State Physics [آشنایی با فیزیک حالت جامد ]. مرکز نشر دانشگاهی. ↑ "Tight binding" . Wikipedia (به انگلیسی). 2024-02-06.↑ Slater, J. C.; Koster, G. F. (1954-06-15). "Simplified LCAO Method for the Periodic Potential Problem" . Physical Review . 94 (6): 1498–1524. doi :10.1103/PhysRev.94.1498 .


 French
French Deutsch
Deutsch





































