چارچوب مرجع - ویکی‌پدیا، دانشنامهٔ آزاد

مکانیک کلاسیک
${\displaystyle {\vec {F}}=m{\vec {a}}}$ قوانین حرکت نیوتن
تاریخچه گاه‌شمار
بخش‌ها کاربردی سماوی محیط‌های پیوسته تحلیلی سینماتیک سینتیک استاتیک آماری
مفاهیم پایه شتاب تکانه زاویه‌ای کوپل اصل دالامبر انرژی انرژی جنبشی انرژی پتانسیل نیرو چارچوب مرجع ضربه لختی / گشتاور لختی جرم (فیزیک) توان کار گشتاور تکانه فضا سرعت زمان گشتاور نیرو سرعت برداری کار مجازی
فرمول‌سازی‌ها قوانین حرکت نیوتن مکانیک تحلیلی مکانیک لاگرانژی مکانیک هامیلتونی Routhian mechanics معادله هامیلتون-ژاکوبی Appell's equation of motion Udwadia–Kalaba equation Koopman–von Neumann mechanics
موضوعات اصلی نوسانگر هماهنگ (نسبت میرایی) بردار جابجایی معادله حرکت قانون حرکت اویلر شبه‌نیرو اصطکاک نوسانگر هماهنگ دستگاه مرجع لخت / دستگاه مرجع غیر لخت حرکت صفحه‌ای ذره حرکت (حرکت خطی) قانون جهانی گرانش نیوتن قوانین حرکت نیوتن سرعت نسبی جسم صلب دینامیک اجسام صلب معادلات اویلر نوسانگر هماهنگ ساده ارتعاش
چرخش به دور محور ثابت حرکت دایره‌ای دستگاه مرجع چرخان نیروی مرکزگرا نیروی گریز از مرکز عکس العمل اثر کوریولیس آونگ سرعت سرعت دورانی شتاب زاویه‌ای / جابه‌جایی زاویه‌ای / بسامد زاویه‌ای / سرعت زاویه‌ای
دانشمندان گالیله نیوتن کپلر جرمایا هاروکس هالی اویلر دالامبر کلرو لاگرانژ لاپلاس همیلتون پواسون دانیل برنولی یوهان برنولی کوشی
ن ب و

در فیزیک و اخترشناسی، چارچوب مرجع به مجموعه‌ای از مختصات و یک مجموعه ساعت‌ها (یا معادل آن) گفته می‌شود که برای اندازه‌گیری مکان، جهت‌گیری و سایر ویژگی‌های فیزیکی اجسام استفاده می‌شود. این مفهوم در بسیاری از زمینه‌های فیزیک، از مکانیک کلاسیک گرفته تا نسبیت خاص و عام، اهمیت دارد.

چارچوب‌های مرجع می‌توانند لَخت (غیر شتاب‌دار) یا غیر لَخت (شتاب‌دار) باشند. در یک چارچوب مرجع لَخت، قوانین حرکت نیوتن صادق هستند و اجسام بدون هیچ نیروی خارجی با سرعت ثابت حرکت می‌کنند. در یک چارچوب مرجع غیر لَخت، نیروهای مجازی مانند نیروی گریز از مرکز و نیروی کوریولیس ظاهر می‌شوند که می‌توانند حرکت اجسام را تحت تأثیر قرار دهند.

انتخاب چارچوب مرجع می‌تواند بر نحوه مشاهده و توصیف پدیده‌های فیزیکی تأثیر بگذارد. برای نمونه، در نسبیت خاص، چارچوب‌های مرجع مختلف می‌توانند منجر به اندازه‌گیری‌های متفاوتی از زمان و طول شوند. این به دلیل پدیده‌های اتساع زمان و انقباض طول است که در سرعت‌های نزدیک به سرعت نور رخ می‌دهند.

در فیزیک، برای سنجیدن مکان، سمت، زمان و دیگر ویژگی‌های یک پدیده، چارچوب مرجع به شکل مجموعه‌ای از محورها استفاده می‌شود. در بررسی حرکت هر ذره نیز باید یک چارچوب مرجع تعیین شود که این چارچوب در فیزیک به عنوان ناظر تعبیر می‌شود. در مورد هر حرکت، چارچوب ویژه‌ای متناسب با نوع حرکت باید بکار رود. این مسئله نه تنها در مورد حرکت بلکه در مورد تمام رویدادها و پدیده‌های فیزیکی مطرح است.^[۱]

برای نمونه برای اینکه بتوان در الکترومغناطیس مقدار نیروی وارد بر یک جسم باردار را محاسبه کرد، ابتدا باید یک چارچوب متناسب با دستگاه تعریف کرده، سپس پدیده را بررسی نمود. اگر این چارچوب مرجع تغییر بکند و به عنوان مثال منتقل شود این مسئله به‌وسیله قواعد تبدیل بیان می‌شود.^[۱]

در فیزیک و اخترشناسی، چارچوب مرجع یک دستگاه مختصات انتزاعی است که مبدأ، گرایش، و تجانس آن توسط مجموعه‌ای از نقاط مرجع مشخص می‌شود - نقظه‌ای که بردار مکان آن هم از نظر ریاضی (با مقادیر مختصات عددی) و هم از نظر فیزیکی (با نشانگرهای مرسوم) مشخص می‌شود.^[۲]

برای n بُعد، n + 1 نقطه مرجع برای تعریف کامل یک چارچوب مرجع کافی است. با استفاده از دستگاه مختصات دکارتی، یک چارچوب مرجع ممکن است با یک نقطه مرجع در مبدأ و یک نقطه مرجع در فاصله یک واحد در امتداد هر یک از n مختصات دستگاه مختصات دکارتی تعریف شود.

در نظریه نسبیت، از چارچوب‌های مرجع برای تعیین رابطه بین یک مشاهده‌گر در حال حرکت و پدیده تحت مشاهده استفاده می‌شود. در این زمینه، این اصطلاح اغلب به چارچوب مرجع مشاهده‌ای (یا قاب مرجع مشاهده‌ای) تبدیل می‌شود، که دلالت بر این دارد که ناظر در چارچوب در حالت سکون است، اگرچه لزوماً در مبدأ آن قرار ندارد. یک چارچوب مرجع نسبیتی شامل (یا دلالت بر) زمان مختصات است، که با چارچوب‌های مرجع مختلف بردار مکان با یکدیگر برابر نیست؛ بنابراین وضعیت با ناوردایی گالیله‌ای متفاوت است، که در آن همه زمان‌های مختصات ممکن اساساً معادل هستند.

نیاز به تمایز بین معانی مختلف «چارچوب مرجع» منجر به اصطلاحات مختلفی شده است. به عنوان مثال، گاهی اوقات نوع دستگاه مختصات به عنوان اصلاح‌کننده اضافه می‌شود، مانند چارچوب مرجع دکارتی. گاهی بر حالت حرکت تأکید می‌شود، مانند در دستگاه مرجع چرخان. گاهی اوقات بر نحوه تبدیل آن به چارچوب‌های که مرتبط تلقی می‌شوند، مانند دستگاه مرجع لخت تأکید می‌شود. گاهی اوقات چارچوب‌ها با مقیاس مشاهداتشان متمایز می‌شوند، مانند چارچوب‌های مرجع ماکروسکوپی و میکروسکوپی.^[۳]

در این مقاله، اصطلاح چارچوب مرجع مشاهده‌ای زمانی استفاده می‌شود که تأکید بر حالت حرکت باشد تا بر انتخاب مختصات یا ویژگی مشاهدات یا دستگاه مشاهده. به این معنا، یک چارچوب مرجع مشاهده‌ای امکان مطالعه تأثیر حرکت بر کل خانواده دستگاه‌های مختصاتی را که می‌توانند به این چارچوب متصل شوند، فراهم می‌کند. از سوی دیگر، یک دستگاه مختصات ممکن است برای بسیاری از اهدافی که وضعیت حرکت دغدغه اصلی نیست، استفاده شود. به عنوان مثال، یک دستگاه مختصات ممکن است برای بهره‌برداری از تقارن یک دستگاه اتخاذ شود. در یک دیدگاه وسیع‌تر، فرمول‌بندی بسیاری از مسائل در فیزیک از مختصات تعمیم‌یافته، مد نرمال یا مقدارویژه و بردارویژه استفاده می‌کند که تنها به‌طور غیرمستقیم با فضا و زمان مرتبط هستند. به نظر می‌رسد که جدا کردن جنبه‌های مختلف یک چارچوب مرجع برای بحث زیر مفید است؛ بنابراین، ما چارچوب‌های مرجع مشاهده‌ای، دستگاه‌های مختصات، و تجهیزات مشاهده‌ای را به عنوان مفاهیم مستقل، جدا می‌کنیم، همان‌طور که در زیر آمده است:

• یک چارچوب مشاهده‌ای (مانند یک دستگاه مرجع لخت یا دستگاه مرجع غیرلخت) یک مفهوم فیزیکی مربوط به حالت حرکت است.
• یک دستگاه مختصات یک مفهوم ریاضی است که به معنای انتخاب زبانی است که برای توصیف مشاهدات استفاده می‌شود.^[۴] در نتیجه، یک ناظر در یک چارچوب مرجع مشاهده‌ای می‌تواند از هر دستگاه مختصاتی (دکارتی، قطبی، منحنی‌الخط، تعمیم‌یافته،...) برای توصیف مشاهدات انجام شده از آن چارچوب مرجع استفاده کند. تغییر در انتخاب این دستگاه مختصات، وضعیت حرکت ناظر را تغییر نمی‌دهد و بنابراین مستلزم تغییر در چارچوب مرجع مشاهده‌ای ناظر نیست. این دیدگاه را می‌توان در جاهای دیگر نیز یافت.^[۵] این موضوع به این معنا نیست که برخی از دستگاه‌های مختصات ممکن است انتخاب بهتری برای برخی مشاهدات نسبت به سایرین باشند.

انتخاب اینکه چه چیزی را اندازه‌گیری کنیم و با چه دستگاه مشاهده‌ای، موضوعی جدا از وضعیت حرکت ناظر و انتخاب دستگاه مختصات است. {{Efn|در اینجا نقل قولی در مورد چارچوب‌های مشاهده‌ای متحرک ${\displaystyle {\mathfrak {R}}}$ و دستگاه‌های مختصات فضای سه بعدی اقلیدسی مرتبط با آن [R, R′, etc.] وجود دارد.^[۶]

«

ما ابتدا مفهوم چارچوب مرجع را معرفی می‌کنیم که خود با ایده ناظر مرتبط است: چارچوب مرجع، به تعبیری، «فضای اقلیدسی حمل شده توسط ناظر» است. اجازه دهید یک تعریف ریاضی‌تر ارائه دهیم:… چارچوب مرجع… مجموعه‌ای از تمام نقاط در فضای اقلیدسی با حرکت جسم صلب ناظر است. گفته می‌شود که چارچوب، مشخص شده با ${\displaystyle {\mathfrak {R}}}$، با ناظر حرکت می‌کند. … موقعیت‌های مکانی ذرات نسبت به یک چارچوب ${\displaystyle {\mathfrak {R}}}$ با ایجاد یک دستگاه مختصات R با مبدأ O برچسب‌گذاری می‌شوند. مجموعه محورهای متناظر که حرکت جسم صلب چارچوب ${\displaystyle {\mathfrak {R}}}$ را به اشتراک می‌گذارند، می‌توانند تحقق فیزیکی ${\displaystyle {\mathfrak {R}}}$ را در نظر بگیرند. در یک چارچوب ${\displaystyle {\mathfrak {R}}}$، مختصات از R به R′ با انجام، در هر لحظه از زمان، همان تبدیل مختصات روی اجزای ذاتی (بردارها و تانسورها) معرفی شده برای نشان دادن کمیت‌های فیزیکی در این چارچوب تغییر می‌کند.

»

و این در مورد سودمندی جداسازی مفاهیم ${\displaystyle {\mathfrak {R}}}$ و [R, R′, etc.]:^[۷]

و این، همچنین در مورد تمایز بین ${\displaystyle {\mathfrak {R}}}$ و [R, R′, etc.]:^[۸]

و از J. D. Norton:^[۹]

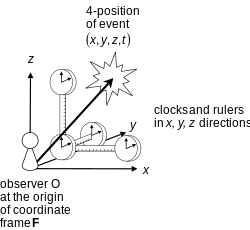
اگرچه اصطلاح «دستگاه مختصات» اغلب (به ویژه توسط فیزیکدانان) به معنای غیر فنی استفاده می‌شود، اما اصطلاح «دستگاه مختصات» در ریاضیات معنای دقیقی دارد و گاهی اوقات منظور فیزیکدان نیز همین است.

یک دستگاه مختصات در ریاضیات وجهی از هندسه یا جبر است،^[۱۰][۱۱] به ویژه، ویژگی منیفلدها (برای مثال، در فیزیک، فضاهای پیکربندی یا فضای فازها).^[۱۲][۱۳] دستگاه مختصات دکارتی یک نقطه r در یک فضای n بعدی به سادگی یک مجموعه مرتب از n عدد است:^[۱۴][۱۵]

${\displaystyle \mathbf {r} =[x^{1},\ x^{2},\ \dots ,\ x^{n}].}$

در یک فضای باناخ کلی، این اعداد می‌توانند (برای مثال) ضرایب در یک بسط تابعی مانند یک سری فوریه باشند. در یک مسئله فیزیکی، آن‌ها می‌توانند مختصات فضازمان یا دامنه‌های مد نرمال باشند. در رباتیک، این اعداد می‌توانند زوایای چرخش‌های نسبی، جابجایی‌های خطی یا تغییر شکل‌های رابط مکانیکی باشند.^[۱۶] در اینجا فرض می‌کنیم که این مختصات را می‌توان با مجموعه‌ای از توابع به یک دستگاه دستگاه مختصات دکارتی مرتبط کرد:

${\displaystyle x^{j}=x^{j}(x,\ y,\ z,\ \dots ),\quad j=1,\ \dots ,\ n,}$

که در آن x, y، z و… n مختصات دکارتی نقطه هستند. با توجه به این توابع، سطوح مختصات توسط روابط زیر تعریف می‌شوند:

${\displaystyle x^{j}(x,y,z,\dots )=\mathrm {constant} ,\quad j=1,\ \dots ,\ n.}$

اشتراک این سطوح خطوط مختصات را تعریف می‌کند. در هر نقطه انتخابی، مماس‌های خطوط مختصات متقاطع در آن نقطه، مجموعه‌ای از بردارهای پایه {e1، e2، ...، en} را در آن نقطه تعریف می‌کنند. به این معنا که:^[۱۷]

${\displaystyle \mathbf {e} _{i}(\mathbf {r} )=\lim _{\epsilon \rightarrow 0}{\frac {\mathbf {r} \left(x^{1},\ \dots ,\ x^{i}+\epsilon ,\ \dots ,\ x^{n}\right)-\mathbf {r} \left(x^{1},\ \dots ,\ x^{i},\ \dots ,\ x^{n}\right)}{\epsilon }},\quad i=1,\ \dots ,\ n,}$

که می‌توان آن را برای داشتن طول واحد نرمال‌سازی کرد. برای جزئیات بیشتر به مختصات خمیده‌خطی مراجعه کنید.

سطوح مختصات، خطوط مختصات و پایه اجزای یک دستگاه مختصات هستند.^[۱۸] اگر بردارهای پایه در هر نقطه متعامد باشند، دستگاه مختصات یک دستگاه مختصات متعامد است.

یک جنبه مهم یک دستگاه مختصات تانسور متریک آن gik است که طول قوس ds را در دستگاه مختصات برحسب مختصات آن تعیین می‌کند:^[۱۹]

${\displaystyle (ds)^{2}=g_{ik}\ dx^{i}\ dx^{k},}$

که در آن شاخص‌های تکرار شده روی آنها جمع می‌شوند.

همان‌طور که از این اظهارات پیداست، یک دستگاه مختصات یک نظریه مدل، بخشی از یک دستگاه اصل موضوعی است. هیچ ارتباط ضروری بین دستگاه‌های مختصات و حرکت فیزیکی (یا هر جنبه دیگری از واقعیت) وجود ندارد. با این حال، دستگاه‌های مختصات می‌توانند زمان را به عنوان یک مختصات شامل شوند و می‌توانند برای توصیف حرکت استفاده شوند؛ بنابراین، تبدیل لورنتسها و تبدیلات گالیله را می‌توان به عنوان دستگاه مختصات مشاهده کرد.

چارچوب مرجع مشاهده‌ای که اغلب به عنوان چارچوب مرجع فیزیکی، چارچوب مرجع یا به سادگی چارچوب نامیده می‌شود، یک مفهوم فیزیکی مربوط به یک ناظر و وضعیت حرکت ناظر است. در اینجا ما دیدگاه بیان شده توسط کومار و بارو را اتخاذ می‌کنیم: یک چارچوب مرجع مشاهده‌ای فقط با وضعیت حرکت آن مشخص می‌شود.^[۲۰] با این حال، در این مورد اتفاق نظر وجود ندارد. در نسبیت خاص، گاهی اوقات بین یک ناظر و یک چارچوب تمایز قائل می‌شوند. بر اساس این دیدگاه، یک چارچوب یک ناظر به اضافه یک شبکه مختصات است که به عنوان مجموعه‌ای از بردارهای فضایی متعامد راست دست عمود بر یک بردار زمان‌مانند ساخته شده است. نگاه کنید به Doran.^[۲۱] این دیدگاه محدود در اینجا استفاده نشده است و حتی در بحث‌های نسبیت نیز به‌طور جهانی پذیرفته نشده است.^[۲۲][۲۳] در [[نسبیت عام] استفاده از دستگاه‌های مختصات عمومی رایج است (برای نمونه، به کارل شوارتزشیلد راه حل میدان گرانشی خارج از یک کره منزوی مراجعه کنید^[۲۴]).

دو نوع چارچوب مرجع مشاهده‌ای وجود دارد: دستگاه مرجع لخت و دستگاه مرجع غیرلخت. یک چارچوب مرجع لَخت به چارچوبی تعریف می‌شود که در آن همه قوانین فیزیک ساده‌ترین شکل خود را دارند. در نسبیت خاص این چارچوب‌ها توسط تبدیل لورنتس مرتبط هستند که توسط سرعت پارامتری می‌شوند. در مکانیک نیوتنی، یک تعریف محدودتر تنها مستلزم آن است که قوانین حرکت نیوتن صادق باشد؛ یعنی یک چارچوب لَخت نیوتنی، چارچوبی است که در آن یک ذره آزاد در یک خط با سرعت ثابت حرکت می‌کند یا در حالت سکون است. این چارچوب‌ها توسط تبدیلات گالیله مرتبط هستند. این تبدیل‌های نسبیتی و نیوتنی در فضاهای با بُعد کلی بر حسب نظریه نمایش گروه‌های Poincaré و Galilean بیان می‌شوند.

چارچوب مرجع لخت به چارچوبی گفته می‌شود که در آن قانون لختی (ماند) حاکم باشد. چارچوب مرجع لخت یکی از نخستین و مهم‌ترین انتزاع‌ها در فیزیک است. چارچوب مرجع واقعی یک چارچوب لخت نیست و می‌توان گفت چارچوبی است که گاهی بیشتر و گاهی کمتر با چارچوب مرجع لخت سازگاری دارد.

برای نمونه چارچوب مرجع وابسته به گرانیگاه زمین نسبت به چارچوب مرجع وابسته به گرانیگاه خورشید کمتر لخت است در حالی که چارچوب مرجع وابسته به هسته کهکشان ما بیشتر از چارچوب مرجع وابسته به خورشید لخت است. بنا به تجربه چارچوب وابسته به ستارگان ثابت بیش از هر چارچوب دیگری لخت است.

بنا بر مکانیک کلاسیک نیوتونی یک چارچوب مرجع لخت اصلی وجود دارد که آن را چارچوب مرجع مطلق می‌نامند که دارای ویژگی‌های اساسی زیر است:

1. چارچوب مرجع مطلق نه به جسم واقعی بلکه به فضای کیهانی وابسته است.
2. چارچوب مرجع مطلق بنا به شرط ساکن است.
3. فضای چارچوب مرجع مطلق فضایی سه بعدی- پیوسته-همگن-همسانگرد و اقلیدسی است.
4. در چارچوب مرجع لخت قوانین نیوتون صدق می‌کند.

هر چارچوب مرجعی که نسبت به چارچوب مرجع مطلق به‌طور یکنواخت و روی خط راست حرکت کند یا ساکن باشد باز هم یک چارچوب مرجع لخت است و از نظر مکانیکی به‌طور کامل با اولی هم ارز است. چارچوب مرجعی که نسبت به چارچوب مرجع مطلق شتاب داشته باشد یک چارچوب مرجع نالخت است.

در مقابل چارچوب لَخت، یک چارچوب مرجع غیرلخت، چارچوبی است که در آن باید شبه‌نیروها برای توضیح مشاهدات فراخوانده شوند. یک مثال، یک چارچوب مرجع مشاهده‌ای است که در نقطه‌ای روی سطح زمین متمرکز شده است. این چارچوب مرجع به دور مرکز زمین می‌چرخد که نیروهای مجازی را معرفی می‌کند که به عنوان اثر کوریولیس، نیروی گریز از مرکز و گرانش شناخته می‌شوند. (همه این نیروها از جمله گرانش در یک چارچوب مرجع واقعاً لَخت که یکی از سقوط آزاد است ناپدید می‌شوند)

جنبه دیگر یک چارچوب مرجع، نقش مترولوژی (به عنوان مثال، ساعت‌ها و میله‌ها) متصل به چارچوب است (به نقل قول نورتون در بالا مراجعه کنید). این سؤال در این مقاله مورد بررسی قرار نگرفته است و مورد توجه خاص در اندازه‌گیری در مکانیک کوانتومی است، جایی که رابطه بین ناظر و اندازه‌گیری هنوز در دست بحث است (به مسئله اندازه‌گیری مراجعه کنید).

در آزمایش‌های فیزیک، چارچوب مرجعی که دستگاه‌های اندازه‌گیری آزمایشگاهی در آن در حالت سکون هستند، معمولاً به عنوان چارچوب آزمایشگاهی نامیده می‌شود. یک مثال می‌تواند چارچوبی باشد که در آن آشکارسازهای یک شتاب‌دهنده ذرات در حالت سکون هستند. چارچوب آزمایشگاهی در برخی آزمایش‌ها یک چارچوب لَخت است، اما لازم نیست که چنین باشد (برای مثال، آزمایشگاه روی سطح زمین در بسیاری از آزمایش‌های فیزیک لَخت نیست). در آزمایش‌های فیزیک ذرات، اغلب مفید است که انرژی‌ها و تکانه‌های ذرات را از چارچوب آزمایشگاهی که در آن اندازه‌گیری می‌شوند، به چارچوب مرکز تکانه "COM frame" که در آن محاسبات گاهی ساده می‌شوند، تبدیل کنیم، زیرا به‌طور بالقوه تمام انرژی جنبشی هنوز در چارچوب COM وجود دارد که ممکن است برای ساخت ذرات جدید استفاده شود.

در این ارتباط ممکن است توجه شود که ساعت‌ها و میله‌هایی که اغلب برای توصیف تجهیزات اندازه‌گیری ناظران در فکر استفاده می‌شود، در عمل با یک مترولوژی بسیار پیچیده‌تر و غیرمستقیم که با ماهیت خلأ مرتبط است، جایگزین می‌شود و از ساعت اتمی استفاده می‌کند که طبق مدل استاندارد کار می‌کنند و باید برای اتساع زمان گرانشی اصلاح شوند.^[۲۵] (به ثانیه، متر و کیلوگرم مراجعه کنید).

در واقع، انیشتین احساس می‌کرد که ساعت‌ها و میله‌ها صرفاً دستگاه‌های اندازه‌گیری مناسبی هستند و باید با موجودیت‌های بنیادی‌تری که بر اساس اتم‌ها و مولکول‌ها هستند، جایگزین شوند.^[۲۶]

بحث فراتر از دستگاه‌های مختصات ساده فضا-زمان توسط Brading و Castellani انجام شده است.^[۲۷] بسط به دستگاه‌های مختصات با استفاده از مختصات تعمیم‌یافته، زیربنای اصل همیلتون و مکانیک لاگرانژی^[۲۸] فرمول‌بندی‌های نظریه میدان‌های کوانتومی، مکانیک کلاسیک و گرانش کوانتومی است.^{[۲۹][۳۰][۳۱][۳۲][۳۳]}

• فیزیک مقدماتی، آی.پی. گورسکی، محمدرضا خوش‌بین، تهران، مبتکران، ج. اول، ۱۳۷۹.
• مدل‌ها و حقایق فیزیک، روبرتو چریانی، مریم ثابت‌قدم، تهران، کانون فرهنگی آموزش، ج اول، ۱۳۸۵.