Morphologie mathématique — Wikipédia

La morphologie mathématique est une théorie et technique mathématique et informatique d'analyse de structures qui est liée avec l'algèbre, la théorie des treillis, la topologie et les probabilités.

Le développement de la morphologie mathématique est inspiré des problèmes de traitement d'images, domaine qui constitue son principal champ d'application. Elle fournit en particulier des outils de filtrage, segmentation, quantification et modélisation d'images. Elle est également utilisable en traitement du signal, par exemple pour filtrer les variations d'une mesure (physique, biologique) au cours du temps.

Une des idées de base de la morphologie mathématique est d'étudier ou de traiter un ensemble à l'aide d'un autre ensemble, appelé élément structurant, qui sert de sonde. À chaque position de l'élément structurant, on regarde s'il touche ou s'il est inclus dans l'ensemble initial. En fonction de la réponse, on construit un ensemble de sortie. On obtient ainsi des opérateurs de base qui sont relativement intuitifs.

Des propriétés que l'on retrouve souvent dans les opérateurs morphologiques sont :

• la non-linéarité ;
• la non-inversibilité ;
• l'idempotence.

Ceci implique en particulier une perte d'information ; bien utilisés, ces opérateurs permettent d'éliminer des structures ne respectant pas certains critères, comme de largeur ou de volume.

La morphologie mathématique s'intéresse aussi aux ensembles et aux fonctions aléatoires.

Le principal domaine d'application de la morphologie mathématique est le traitement d'images. Elle fournit, en particulier, des outils de filtrage, de segmentation et de quantification. Depuis son apparition, en 1964, elle connaît un succès grandissant et désormais contribue à garnir la boite à outils de tout traiteur d'images.

La morphologie mathématique a été inventée en 1964 par Georges Matheron et Jean Serra dans les laboratoires de l'école des Mines de Paris. Son développement a toujours été fortement motivé par des applications industrielles. Dans un premier temps, il s'est agi de répondre à des problèmes dans le domaine de l'exploitation minière, mais très vite ses champs d'applications se sont diversifiés : biologie, imagerie médicale, sciences des matériaux, vision industrielle, multimédia, télédétection et géophysique constituent quelques exemples de domaines dans lesquels la morphologie mathématique a apporté une contribution importante.

La morphologie mathématique reste un domaine actif de recherche. En témoignent les nombreuses publications scientifiques sur le sujet, ainsi que les symposiums internationaux sur la morphologie mathématique qui ont lieu tous les deux ou trois ans.

Quelques exemples de thèmes de recherche actuels :

• ligne de partage des eaux : parallélisation, approche topologique, hiérarchisation ;
• extension à des espaces non-euclidiens, à des fonctions vectorielles (images en couleurs, images multi-spectrales, etc.) et à des images non conventionnelles;
• liens avec l'apprentissage profond (réseaux morphologiques; pré-traitement et post-traitement);
• approches stochastiques pour la segmentation et le filtrage;
• architectures électroniques efficaces pour l'implantation d'opérateurs morphologiques;
• développement d'algorithmes rapides;
• traitement de nuages de points;
• modélisation de structures physiques, en particulier dans le domaine des sciences des matériaux.

La morphologie mathématique peut être développée dans le cadre abstrait de la théorie des treillis. Cependant, une présentation plus pratique, visant un utilisateur potentiel d'outils de traitement d'images, plutôt qu'un mathématicien, est ici adoptée.

Plaçons-nous dans ${\displaystyle E=\mathbb {Z} ^{2}}$, souvent utilisé comme modélisation du support des images binaires à deux dimensions, même si tout ce qui est présenté dans cette section reste valable dans ${\displaystyle \mathbb {R} ^{d}}$, où ${\displaystyle d}$ est un entier strictement positif. Soit ${\displaystyle B}$ un sous-ensemble de ${\displaystyle E}$, appelé élément structurant. Si ${\displaystyle x}$ est un élément de ${\displaystyle E}$, alors nous noterons ${\displaystyle B_{x}}$ l'ensemble ${\displaystyle B}$ translaté de ${\displaystyle x}$ : ${\displaystyle B_{x}=\{b+x\mid b\in B\}}$

L'élément structurant joue en quelque sorte le rôle de modèle local, ou de sonde. Il est promené partout sur l'image à traiter, et à chaque position on étudie sa relation avec l'image binaire, considérée comme un ensemble. Ces relations peuvent être du type « est inclus dans l'ensemble », ou « touche l'ensemble », par exemple.

En pavage carré, les éléments structurants les plus classiquement utilisés sont la croix, constituée de l'origine et des quatre points les plus proches, et le carré, constitué de l'origine et des huit points les plus proches. Ces deux éléments structurants correspondent respectivement à deux définitions possibles du voisinage d'un pixel ou du type de connexité de l'image. En pavage hexagonal, l'élément de base est l'hexagone centré.

On introduit aussi le symétrique d'un ensemble, noté ${\displaystyle {\breve {B}}}$ : ${\displaystyle {\breve {B}}=\{-b\mid b\in B\}}$

Si ${\displaystyle B}$ est symétrique, on a ${\displaystyle {\breve {B}}=B}$.

Soit ${\displaystyle X}$ un sous-ensemble de ${\displaystyle E}$. La dilatation morphologique avec l'élément structurant ${\displaystyle B}$ est définie comme la somme de Minkowski^[1]: ${\displaystyle \delta _{B}(X)=X\oplus B=\{x+b\mid b\in B,x\in X\}=\cup _{x\in X}B_{x}}$

Une autre formulation plus intuitive est : ${\displaystyle \delta _{B}(X)=\{x\mid {\breve {B}}_{x}\cap {X}\neq \emptyset \}}$

La dilatation morphologique n'est, en général, pas inversible. L'opération qui en quelque sorte tente de produire l'inverse de la dilatation est l'érosion morphologique: ${\displaystyle \epsilon _{B}(X)=X\ominus B=\{x\mid B_{x}\subset X\}}$

La dilatation et l'érosion sont les opérateurs de base de la morphologie mathématique. Pratiquement tous les autres peuvent être définis à l'aide de ceux-ci, en utilisant des compositions de fonctions et des opérations ensemblistes.

• 
  Image originale (en noir : l'objet ; en blanc : le fond).
• 
  Dilatation par un carré 3x3 : les pixels noirs et gris font partie de l'ensemble résultant.
• 
  Érosion par un carré 3x3 : seuls les pixels noirs font partie de l'ensemble résultant.

La dilatation est une transformation extensive si B contient l’origine : ${\displaystyle X\subseteq \delta _{B}(X)}$L’érosion est anti-extensive si B contient l'origine : ${\displaystyle \epsilon _{B}(X)\subseteq X}$La dilatation et l’érosion sont des transformations croissantes (comme l’union et l’intersection) : ${\displaystyle X\subseteq Y\Rightarrow \delta _{B}(X)\subseteq \delta _{B}(Y)}$${\displaystyle X\subseteq Y\Rightarrow \epsilon _{B}(X)\subseteq \epsilon _{B}(Y)}$La dilatation et l’érosion ne sont pas des transformations idempotentes : ${\displaystyle \delta _{B}(\delta _{B}(X))\neq \delta _{B}(X)}$${\displaystyle \epsilon _{B}(\epsilon _{B}(X))\neq \epsilon _{B}(X)}$Par contre la dilatation et l’érosion vérifient la propriété d’itérativité qui permet de construire des dilatations ou des érosions avec des éléments structurants homothétiques : ${\displaystyle \delta _{3B}(X)=\delta _{1B}(\delta _{1B}(\delta _{1B}(X)))}$${\displaystyle \epsilon _{3B}(X)=\epsilon _{1B}(\epsilon _{1B}(\epsilon _{1B}(X)))}$La dilatation est une transformation continue et l’érosion est une transformation semi-continue supérieure. Cette propriété découle directement de la propriété de l’intersection dans la soustraction de Minkowski.

La dilatation est distributive par rapport à l’union et l’érosion par rapport à l’intersection : ${\displaystyle \delta _{B\cup B'}(X)=\delta _{B}(X)\cup \delta _{B'}(X)}$${\displaystyle \epsilon _{B\cap B'}(X)=\epsilon _{B}(X)\cap \delta _{B'}(X)}$Soit une famille d’éléments structurants homothétiques et une homothétie de rapport ${\displaystyle \lambda }$. La compatibilité de la dilatation et de l’érosion avec les homothéties s’écrivent : ${\displaystyle \delta _{1B}(X)={\frac {1}{\lambda }}\delta _{\lambda B}(\lambda X)}$${\displaystyle \epsilon _{1B}(X)={\frac {1}{\lambda }}\epsilon _{\lambda B}(\lambda X)}$

La dilatation, comme l’union, préserve la connexité. La dilatation n’est pas une transformation qui préserve l’homotopie. En effet, elle connecte des éléments disjoints et bouche des trous. L’érosion n’est pas une transformation qui préserve l’homotopie. En effet, elle sépare les parties connexes et supprime des éléments lorsqu’ils sont petits. L’érosion, comme l’intersection, ne préserve pas la connexité.

La composition d'une dilatation morphologique avec l'érosion par le même élément structurant ne produit pas, en général, l'identité, mais deux autres opérateurs morphologiques, l'ouverture morphologique : ${\displaystyle \gamma _{B}(X)=X\circ B=\delta _{B}(\epsilon _{B}(X))}$ et la fermeture morphologique : ${\displaystyle \phi _{B}(X)=X\bullet B=\epsilon _{B}(\delta _{B}(X))}$L'ouverture peut être caractérisée géométriquement: elle donne l'union de tous les ${\displaystyle B_{x}}$ inclus dans ${\displaystyle X}$. Ainsi, la forme de l'élément structurant permet de choisir les structures qui peuvent le contenir.

La fermeture est le dual de l'ouverture : la fermeture du complémentaire d'un ensemble est égale au complémentaire de l'ouverture de cet ensemble.

On notera que si l'élément structurant ${\displaystyle B}$ n'est pas symétrique, on devra utiliser l'élément symétrique ${\displaystyle {\breve {B}}}$ pour le second opérateur (dilatation dans le cas de l'ouverture et érosion dans le cas de la fermeture).

• La fermeture et l'ouverture sont des opérations croissantes et idempotentes, deux propriétés qui définissent les filtres morphologiques.
• La fermeture est extensive (${\displaystyle X\subset \phi (X)}$), et l'ouverture est anti-extensive (${\displaystyle \gamma (X)\subset X}$).
• L’ouverture et la fermeture sont des opérateurs semi-continu supérieur. C’est l’érosion qui impose cette propriété, la dilatation étant continue.
• Du point de vue topologique, l’ouverture ne préserve pas la connexité alors que la fermeture la préserve. L’ouverture et la fermeture ne sont pas des transformations homotopiques.

• 
  Image originale
• 
  Fermeture par un carré 3×3 : les pixels noirs et gris font partie de l'ensemble résultant
• 
  Ouverture par un carré 3×3 : seuls les pixels noirs font partie de l'ensemble résultant

On peut aussi prendre deux éléments structurants ${\displaystyle A}$ et ${\displaystyle B}$ pour définir des transformations. Si on demande en chaque point ${\displaystyle x}$ à ${\displaystyle A}$ d'être à l'extérieur de l'ensemble et à ${\displaystyle B}$ à l'intérieur on obtient la transformation en tout ou rien (hit or miss transform en anglais) : ${\displaystyle \eta (X)=\{x\mid A_{x}\subset X^{c};B_{x}\subset X\}}$ où ${\displaystyle X^{c}}$ désigne le complémentaire de l'ensemble ${\displaystyle X}$. Cette transformation permet de détecter certaines configurations précises de pixels. Parmi  les configurations les plus utilisées on aura :

• Les points extrêmes et les points triples du squelette obtenu par amincissement.
• Les configurations correspondant aux différents nombres de connexités.

En ajoutant le résultat de la transformation à l'ensemble initial on obtient un épaississement : ${\displaystyle \operatorname {ep} (X)=X\cup \eta (X)}$en enlevant le résultat de l'ensemble initial on obtient un amincissement : ${\displaystyle \operatorname {aminc} (X)=X-\eta (X)}$

• En prenant des suites d'amincissements, on peut réduire progressivement l'ensemble initial (comme si on l'épluchait). De cette façon on peut calculer différents types de squelettes, dont des squelettes homotopiques.
• Des épaississements homotopiques permettent aussi de construire des Skiz (squelettes par zone d’influence).
• Avec une autre configuration on pourra obtenir par épaississement les enveloppes convexes.

Une image à niveaux de gris peut être modélisée comme une fonction de ${\displaystyle \mathbb {Z} ^{2}}$ dans ${\displaystyle \mathbb {Z} }$. Soit ${\displaystyle f}$ une fonction appartenant à cet ensemble. On a alors :

${\displaystyle \delta _{B}(f)=\sup\{f_{b}\mid b\in B\}}$

${\displaystyle \epsilon _{B}(f)=\inf\{f_{b}\mid b\in B\}}$

L'ouverture et la fermeture de fonctions s'obtiennent comme dans le cas ensembliste :

${\displaystyle \gamma _{B}(f)=\delta _{B}\,\epsilon _{B}(f)}$

${\displaystyle \phi _{B}(f)=\epsilon _{B}\,\delta _{B}(f)}$

L'ouverture et la fermeture morphologiques constituent déjà des outils intéressants de filtrage d'images. Cependant, ils peuvent modifier le contour des objets, propriété qui peut être malvenue. Les opérateurs par reconstruction et plus généralement les nivellements, introduits plus loin, permettent de pallier cet inconvénient.

Épaississements et amincissements ne sont pas, en général, des opérateurs croissants. Par conséquent, leur application aux fonctions (en pratique, aux images à niveaux de gris) n'est pas triviale. Plusieurs extensions ont été proposées dans la littérature.

La détection de contours représente une tâche importante en traitement d'images. La morphologie mathématique propose des outils non-linéaires de détection de contours, comme le gradient et le laplacien morphologiques.

Le gradient morphologique, aussi appelé gradient de Beucher du nom de son inventeur, est défini par :

${\displaystyle \operatorname {grad} _{B}(X)=\delta _{B}(X)-\epsilon _{B}(X)}$

Il correspond, en quelque sorte, à la version morphologique du module du gradient euclidien.

Le laplacien morphologique est construit de façon analogue :

${\displaystyle \operatorname {lap} _{B}(X)=\delta _{B}(X)+\epsilon _{B}(X)-2\operatorname {id} (X)}$

où ${\displaystyle \operatorname {id} }$ correspond à l'opérateur identité.

Tous les opérateurs définis dans les sections précédentes l’ont été dans un cadre euclidien à savoir que l’espace de définition de l’image sert de référence pour les opérateurs. Dans cette section, on va reprendre les deux opérateurs de base que sont l’érosion et la dilatation mais en restant dans un sous espace ${\displaystyle X}$ de ${\displaystyle \mathbb {E} }$, nommé espace de référence. Les transformations euclidiennes deviendront ainsi des transformations géodésiques (appelées aussi transformations conditionnelles).

La géodésie est la science de la mesure de la forme et des dimensions de la terre. Ainsi une distance géodésique correspond au chemin le plus court pour aller d’un point à un autre en restant à la surface du globe. La longueur de ce chemin, à la différence de la distance euclidienne, ne correspond pas à un segment droit mais à celle d’un arc géodésique. La définition d’arc géodésique implique la notion de connexité par arc. Un espace topologique ${\displaystyle \mathbb {E} }$ est dit connexe par arcs si tout couple de points de ${\displaystyle \mathbb {E} }$ est relié par un chemin dont le support est inclus dans ${\displaystyle \mathbb {E} }$.

La distance géodésique utilise les mêmes axiomes que la distance euclidienne, seul, le chemin est différent.

Soit quatre points ${\displaystyle \left\{x_{1},x_{2},x_{3},x_{4}\right\}\in X}$.

Sur la partie gauche de l’image, on a représenté les segments de droite associés aux différentes distances euclidiennes. Sur la partie droite, on a représenté les trois arcs géodésiques reliant ${\displaystyle x_{1},x_{2}}$ et ${\displaystyle x_{3}}$. On remarque que le point ${\displaystyle x_{4}}$ ne possède aucun chemin géodésique car il appartient à une composante disjointe de celle contenant les trois autres points.

La distance géodésique vérifie bien les axiomes d’une distance. On a, en effet : ${\displaystyle d_{X}(x_{1},x_{2})=d_{X}(x_{2},x_{1})}$${\displaystyle x_{1}=x_{2}\Rightarrow d_{X}(x_{1},x_{2})=0}$${\displaystyle d_{X}(x_{1},x_{3})\leq d_{X}(x_{1},x_{2})+d_{X}(x_{2},x_{3})}$

À ces axiomes, il faut ajouter un quatrième. Lorsqu'il n’y a aucun chemin géodésique, on a :${\displaystyle d_{X}(x_{1},x_{4})=\infty }$Pour les mêmes points, il est possible de comparer les distances géodésiques par rapport à ${\displaystyle X}$ et les distances euclidiennes. On aura toujours une distance géodésique plus grande ou égale à la distance euclidienne avec la possibilité d’avoir une distance euclidienne finie et une distance géodésique infinie :${\displaystyle d_{X}(x_{1},x_{2})\geq d(x_{1},x_{2})}$On notera au passage que, pour relier deux points, il peut y avoir plusieurs arcs géodésiques équivalents, alors que le chemin euclidien est unique.

Dans ${\displaystyle \mathbb {R} ^{2}}$ l’élément structurant isotrope centré en ${\displaystyle x}$ et de taille ${\displaystyle \lambda }$ est le disque fermé ${\displaystyle \lambda B}$, défini par :${\displaystyle \lambda B_{x}=\left\{y:d(x,y)\leq \lambda \right\}}$Le disque géodésique, ${\displaystyle \lambda B_{X}}$ se définit par rapport à l’ensemble de référence ${\displaystyle X}$ en remplaçant la distance euclidienne par la distance géodésique par rapport à ${\displaystyle X}$. On a alors :${\displaystyle (\lambda B_{X})_{x}=\left\{y:d_{X}(x,y)\leq \lambda \right\}}$

La figure ci-contre illustre la différence qui existe entre un élément structurant euclidien et un élément structurant géodésique. Sur cette figure, on a placé le disque ${\displaystyle B}$ sur différentes positions ${\displaystyle x_{1},x_{2},x_{3},x_{4},x_{5}}$. Le disque euclidien reste le même indépendamment de la position x. Par contre, le disque géodésique change de forme ou peut disparaître en fonction de sa position. Du disque initial, il ne reste que ce qui vérifie la distance géodésique. Ainsi les points du disque qui ne sont pas commun avec ${\displaystyle X}$ sont ignorés (positions ${\textstyle x_{3},x_{4}}$). Si le centre du disque n’appartient pas à ${\displaystyle X}$, alors le disque géodésique n’existe pas (${\displaystyle x_{5}}$).

En plus de l’ensemble à transformer que l’on appellera ${\displaystyle M}$ (pour marqueur), il faut introduire l’ensemble de référence géodésique ${\displaystyle X}$.

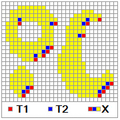
On part de la définition euclidienne de la dilatation en remplaçant la boule euclidienne par la boule géodésique. On peut alors écrire : ${\displaystyle \delta _{X,B}(M)=\left\{z:(B_{X})_{z}\Uparrow M\right\}=\left\{z:(B_{X})_{z}\cap M\neq \emptyset \right\}}$Ensuite, on répète cette opération élémentaire ${\displaystyle \lambda }$ fois : ${\displaystyle \delta _{X,nB}(M)=\delta _{X,1B}(...\delta _{X,1B}(\delta _{X,1B}(M))...)}$ Les figures suivantes illustrent l’effet d’une dilatation géodésique par un hexagone. Une composante connexe de l’ensemble ${\displaystyle M}$ ne peut être dilaté que si elle intersecte ${\displaystyle X}$, sinon elle disparaît. La dilatation s’arrête lorsque les frontières de ${\displaystyle X}$ sont atteintes.

• 
  Ensemble de référence X (jaune et rouge) et marqueur M (rouge et bleu)
• 
  Dilatation géodésique (hexagone taille 15) de M dans X
• 
  Dilatation géodésique (hexagone taille 40) de M dans X

L’ensemble ${\displaystyle X}$ se comporte comme un masque dans lequel on peut modifier ${\displaystyle M}$ et ${\displaystyle M}$ se comporte comme un marqueur permettant d’envahir une composante connexe de ${\displaystyle X}$.

De la même manière, on introduit l’érosion géodésique en remplaçant la boule euclidienne par la boule géodésique dans l’expression définissant l’érosion. On peut donc écrire :${\displaystyle \epsilon _{X,B}(M)=\left\{z:(B_{X})_{z}\subseteq M\right\}}$Comme l’élément structurant utilisé est symétrique, on a dualité entre l’érosion et la dilatation géodésique. Cette dualité s’exprime de manière légèrement différente de celle du cas euclidien car c’est le complémentaire par rapport à ${\displaystyle X}$ qu’il faut prendre en compte. Cette relation de dualité s’écrit alors avec l’opérateur de différence symétrique :${\displaystyle \epsilon _{X,B}(M)=X/\delta _{X,B}(X/M)}$Les figures illustrent l’effet de l’érosion géodésique sur un ensemble ${\displaystyle M}$ par rapport à ${\displaystyle X}$ en utilisant un élément structurant hexagonal.

• 
  Ensemble de référence X (jaune et rouge) et marqueur M (rouge)
• 
  Érosion géodésique (hexagone taille 15) de M dans X

On remarque que les parties de ${\displaystyle M}$, totalement incluses dans ${\displaystyle X}$ et n’ayant pas de frontières communes, s’érodent comme dans le cas euclidien. Lorsqu’il y a des frontières communes, celles-ci ne sont pas affectées par l’érosion.

La reconstruction d’un ensemble à partir d’un autre est une des principales applications de la dilatation géodésique. On part donc de deux ensembles ; le premier est appelé l’ensemble des marqueurs noté ${\displaystyle M}$, le second est l’ensemble de référence ou masque ${\displaystyle X}$. Par définition, la reconstruction est une dilatation géodésique infinie, par rapport à ${\displaystyle X}$, des marqueurs ${\displaystyle M}$. Cela s’écrit :${\displaystyle \gamma ^{Rec}(M:X)=\delta _{X,\infty B}(M)}$Lorsque toutes les composantes connexes contenant des marqueurs seront envahies, on ne pourra plus modifier l’image. Ceci constitue le test d’arrêt de la procédure. Les figures suivantes illustrent la reconstruction de ${\displaystyle X}$ à partir des marqueurs ${\displaystyle M}$.

• 
  Ensemble de référence X (jaune et rouge) et marqueur M (rouge)
• 
  Reconstruction de X à partir des marqueurs M

• La reconstruction est idempotente : la reconstruction s’arrêtant lorsque l’on ne modifie plus rien, elle vérifie cette propriété.

• La reconstruction est anti-extensive par rapport à ${\displaystyle X}$ : ne sont reconstruites que les composantes connexes contenant un marqueur.${\displaystyle \gamma ^{Rec}(M:X)\subseteq X}$
• La reconstruction est croissante :${\displaystyle X_{1}\subset X_{2}\Rightarrow \gamma ^{Rec}(M:X_{1})\subset \gamma ^{Rec}(M:X_{2})}$La reconstruction correspond donc à une ouverture algébrique de l’ensemble de référence.

• La reconstruction est idempotente

• La reconstruction est extensive par rapport à ${\displaystyle M}$ :${\displaystyle \gamma ^{Rec}(M:X)\supseteq M}$
• La reconstruction est croissante :${\displaystyle M_{1}\subset M_{2}\Rightarrow \gamma ^{Rec}(M_{1}:X)\subset \gamma ^{Rec}(M_{2}:X)}$

La reconstruction correspond donc à une fermeture algébrique des marqueurs.

On ne citera ici que les plus importantes.

Dans l’érosion-reconstruction, les marqueurs ${\displaystyle M}$ seront les érodés euclidiens de ${\displaystyle X}$ et la dilatation euclidienne sera remplacée par la dilatation géodésique des marqueurs par rapport à l’ensemble ${\displaystyle X}$. Cela s’écrit :${\displaystyle \gamma _{\lambda B}^{Rec}(X)=\gamma ^{Rec}(\epsilon _{\lambda B}(X):X)}$Cette érosion-reconstruction est illustrée par les figures suivantes et comparée avec l’ouverture géodésique utilisant le même élément structurant.

• 
  Ensemble X1 (jaune et rouge) et érosion hexagonale de taille 11 (M1 = rouge)
• 
  Reconstruction de X1 à partir de M1
• 
  Ouverture géodésique de X1 (rouge : hexagone de taille 11)

Pour certaines applications analytiques, il est nécessaire d’éliminer les composantes connexes de ${\displaystyle X}$ qui coupent le bord du champ d’observation ${\displaystyle Z}$. Pour cela, il faut les isoler en les reconstruisant à partir d’un marqueur constitué de tous les pixels du bord du champ ${\displaystyle Z}$, noté ${\displaystyle M=\partial Z}$ et les soustraire de ${\displaystyle X}$. La procédure va donc être la suivante :${\displaystyle Y=X/\gamma ^{Rec}(\partial Z:X)}$L’ensemble ${\displaystyle Y}$ ne contient que des composantes connexes totalement incluses dans ${\displaystyle Z}$. Ceci est illustré par les figures suivantes.

• 
  Ensemble X2 (jaune) et bord du champ dZ (rouge)
• 
  Composantes connexes de X2 reconstruites, coupant le bord du champ (rouge)
• 
  Composantes connexes de X2 totalement incluses dans le champ Z

La reconstruction est utilisée dans une opération qui sert souvent en traitement d’image : le bouchage de trous. Comme dans l’application précédente, le marqueur est ${\displaystyle M=\partial Z}$. L’algorithme est le suivant :${\displaystyle Y=\left(\gamma ^{Rec}(\partial Z:X^{C})\right)^{C}}$Les figures suivantes illustrent la séquence d’opérations.

• 
  Ensemble X3 (jaune) et bord du champ dZ (rouge)
• 
  Complémentaire de l'ensemble X3 (jaune) et bord du champ dZ (rouge)
• 
  Reconstruction du complémentaire de X3 à partir de dZ
• 
  Bouchage des trous de X3

• Définition

Soit un ensemble ${\displaystyle X}$ présenté sur la figure suivante. Les érodés ultimes apparaissent au cours d’une succession d’érosions de ${\displaystyle X}$ par un élément structurant ${\displaystyle B}$ convexe. Ils sont constitués par l’union des composantes connexes qui disparaissent lors de l’érosion de taille immédiatement supérieure.

Soit ${\displaystyle \epsilon _{1B}}$ une érosion digitale élémentaire, et ${\displaystyle \epsilon _{iB}}$ son itérée d'ordre i. L'érosion ultime dérivée de ${\displaystyle \epsilon }$ et notée ${\displaystyle U_{i}(X)}$ se définit alors comme le ‘’résidu’’ entre ${\displaystyle \epsilon _{iB}}$ et les ouvertures par reconstruction de chaque érosion dans la précédente :${\displaystyle U_{i}(X)=\epsilon _{iB}(X)/\gamma ^{Rec}(\epsilon _{(i+1)B}(X):\epsilon _{iB(X)})}$Les érodés ultimes correspondent à l’union de toutes ces reconstructions en faisant varier de 1 à imax lorsqu’il n’y a plus rien par érosion.${\displaystyle U(X)=\bigcup _{i}(U_{i}(X))}$

• Propriétés des érodés ultimes
  • L’érosion ultime est anti extensive.
  • Les éléments constituants l’ensemble des érodés ultimes sont disjoints.
  • Une érosion unitaire sur les érodés ultime donne un ensemble vide.
  • L’érosion ultime est idempotente.

Ces érodés ultimes peuvent également être obtenus à partir des maxima de la fonction distance en utilisant une méthode géodésique pour les fonctions que l’on voit ci après. En restant dans le domaine ensembliste, les érodés ultimes servent à marquer les parties convexes des objets et peuvent être utilisés pour segmenter des agrégats de particules convexes.

Comme pour le cas ensembliste, on aura une fonction de référence ${\displaystyle f(x)}$ et une fonction qui sera transformée ${\displaystyle m(x)}$. Les deux opérateurs de base sont toujours la dilatation géodésique et l’érosion géodésique.

La dilatation géodésique élémentaire de ${\displaystyle m(x)}$ sous ${\displaystyle f(x)}$ s’exprime de manière analogue à celle utilisée pour les ensembles.

Dans le cas des fonctions, ces éléments seront des éléments plats et convexes isotropes. On a, en effet :${\displaystyle \delta _{f,1B}(m(x))=\delta _{1B}(m(x))\wedge f(x)}$Pour une dilatation géodésique de taille quelconque, on aura également :${\displaystyle \delta _{f,\lambda B}(m(x))=\delta _{f,1B}(...\delta _{f,1B}(m(x))...)}$

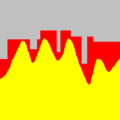
Les images en niveaux de gris sont des fonctions ${\displaystyle f(x)}$ définies dans ${\displaystyle \mathbb {R} ^{2}\times \mathbb {R} }$. Pour faciliter la vision du comportement des opérateurs, on va utiliser une fonction ${\displaystyle f(x)}$ définie dans ${\displaystyle \mathbb {R} ^{1}\times \mathbb {R} }$. Soit également une fonction ${\displaystyle m(x)}$ définie dans le même espace. Pour notre exemple, la seule possibilité est un ‘’élément structurant plat’’ constitué d’un ‘’segment droit’’ de longueur ${\displaystyle \lambda }$ centré.

Les figures suivantes illustrent le cas d’une dilatation géodésique de taille ${\displaystyle \lambda =2n+1}$.

• 
  Fonction f(x) (jaune et rouge) et marqueurs m1(x) (rouge)
• 
  Dilatation de taille 20 des marqueurs m1(x) (rouge) sous la fonction f(x) (jaune et rouge)

On remarque que les marqueurs dilatés restent toujours sous la fonction ${\displaystyle f(x)}$. Avec un élément structurant plat, il reste des parties de ${\displaystyle f(x)}$ qui sont inaccessibles à la dilatation. Ce sont des parties convexes incluant les maxima.

On remarque que les marqueurs sont généralement choisis de telle sorte que l’on ait :${\displaystyle m(x)<f(x)}$

Par définition, l’érosion géodésique élémentaire est donnée par :${\displaystyle \epsilon _{f,1B}(m(x))=\epsilon _{1B}(m(x))\vee f(x)}$Comme pour la dilatation géodésique, on aura par itération :${\displaystyle \epsilon _{f,\lambda B}(m(x))=\epsilon _{f,1B}(...\epsilon _{f,1B}(m(x))...)}$L’érosion géodésique pour les fonctions se déduit également de la dilatation géodésique pour les fonctions par dualité. Appelons ${\displaystyle M}$ ‘’le niveau de gris maximum supporté par l’image’’. On aura alors :

${\displaystyle \epsilon _{f,B}(m(x))=M-\delta _{f,B}(M-m(x))}$

Cette expression est d’ailleurs celle utilisée pour construire n’importe quelle érosion géodésique.

Les figures illustrent le comportement de l’érosion géodésique pour une fonction ${\displaystyle \mathbb {R} ^{1}\times \mathbb {R} }$.

• 
  Fonction f(x) (jaune) et marqueurs m2(x) (jaune et rouge)
• 
  Érosion de taille 15 des marqueurs m2(x) (jaune et rouge) sur la fonction f(x) (jaune)

On remarque que la fonction érodée conserve des résidus dans les parties concaves de la fonction ${\displaystyle f(x)}$. Ce résultat est symétrique de celui obtenu par dilatation géodésique.

Comme nous l’avons fait pour les ensembles, il est possible de reconstruire des fonctions géodésiquement par rapport à une autre fonction. Deux cas sont à envisager.

• La reconstruction de ${\displaystyle m(x)sousf(x)}$ par dilatation géodésique infinie (ouverture)

${\displaystyle \gamma ^{Rec}(m(x):f(x))=\delta _{f,\infty B}(m(x))}$

• La reconstruction de ${\displaystyle m(x)surfx)}$ par érosion géodésique infinie (fermeture)

${\displaystyle \varphi ^{Rec}(m(x):f(x))=\epsilon _{f,\infty B}(m(x))}$

La première figure illustre le résultat obtenu dans le cas de la reconstruction de ${\displaystyle m1}$ sous la fonction ${\displaystyle f}$ et la seconde figure, la reconstruction de ${\displaystyle m2}$ sur la fonction ${\displaystyle f}$.

• 
  Reconstruction des marqueurs m1(x) (rouge) sous la fonction f(x) (jaune et rouge)
• 
  Reconstruction des marqueurs m2(x) (jaune et rouge) sur la fonction f(x) (jaune)

Les maxima régionaux d’une image sont les points de l’image à partir desquels il n’existe que des chemins descendants. Soit ${\displaystyle f(x)}$ une image. À partir de cette image, on va construire une image des marqueurs ${\displaystyle m(x)}$ en soustrayant un niveau de gris à ${\displaystyle f(x)}$. on aura donc :${\displaystyle m(x)=f(x)-1}$Ensuite, on effectue une reconstruction de ${\displaystyle m(x)}$ sous ${\displaystyle f(x)}$ et par différence avec ${\displaystyle f(x)}$, on obtient les maxima régionaux. On a donc :${\displaystyle Max(f(x))=f(x)-\gamma ^{rec}(f(x)-1:f(x))}$

Pour la recherche des minima régionaux d’une fonction, on applique le même principe. Tout d’abord, on forme l’image des marqueurs :${\displaystyle m(x)=f(x)+1}$Ensuite, on effectue une reconstruction de ${\displaystyle m(x)}$ sur ${\displaystyle f(x)}$ et par différence avec ${\displaystyle f(x)}$, on obtient les minima régionaux. On a donc :${\displaystyle Max(f(x))=f(x)-\varphi ^{rec}(f(x)+1:f(x))}$

La recherche des maxima et minima d’une fonction donnent de très bons résultats si l’image n’est pas bruitée. En présence de bruit, la notion de maxima et de minima étendus, appelés aussi Hmax et Hmin, permet de n’extraire d’une image que les extrema significatifs. L’algorithme est semblable à celui des maxima et des minima. Seule, la construction des marqueurs est légèrement différente. En effet, au lieu de translater l’image d’un niveau de gris (en moins ou en plus), on effectue une translation de h niveaux de gris en plus ou en moins. Les Hmax et Hmin s’écrivent alors de la manière suivante.${\displaystyle Hmax(f(x))=f(x)-\gamma ^{rec}(f(x)-h:f(x))}$${\displaystyle Hmin(f(x))=f(x)-\varphi ^{rec}(f(x)+h:f(x))}$

Les figures suivantes illustrent la construction des Hmax dans le cas d’une fonction ${\displaystyle \mathbb {R} ^{1}\times \mathbb {R} }$.

• 
  Fonction f(x) (jaune et rouge) et marqueurs m(-h) (rouge)
• 
  Fonction (fx) (jaune et rouge) et Hmax de f(x) (rouge)

A titre d’exemple, on montre le résultat dans le cas de l’image d’un pavage en niveaux de gris bruité. Les maxima régionaux de ce pavage sont inutilisables à cause du bruit. Par contre, les Hmax permettent de visualiser les plateaux de chaque pavé.

• 
  Image (en niveaux de gris) d'un pavage bruité
• 
  Maxima du pavage bruité
• 
  Hmax (h=30) du pavage bruité
• 
  Filtrage morphologique des Hmax par une ouverture de taille 1 suivie d'une fermeture de taille 10.

La recherche des maxima significatifs peut être améliorée par un filtrage de l’image binaire résultante, comme le montre la figure suivante. Les ‘’Hmin’’ sont obtenus et traités de manière analogue.

Segmenter une image à niveaux de gris consiste à produire une partition du support de l'image, de façon que les régions de la partition correspondent aux objets présents dans l'image.

Les filtres morphologiques constituent une aide précieuse dans un processus de segmentation. En particulier, les nivellements permettent de filtrer les images tout en préservant les contours importants, ce qui simplifie l'opération de segmentation proprement dite. Dans certains cas, un filtrage important peut de lui-même produire une partition pertinente. Mais l'outil morphologique le plus connu en segmentation d'images est la ligne de partage des eaux.

Il existe plusieurs algorithmes de segmentation par ligne de partage des eaux. L'idée de base consiste à simuler une inondation de l'image, vue comme un relief topographique où le niveau de gris correspond à l'altitude. Les frontières entre régions de la partition ont alors tendance à se placer sur les lignes de crête. Typiquement, on applique cet opérateur au gradient de l'image (norme du gradient euclidien, ou gradient morphologique) que l'on cherche à segmenter, et par conséquent les frontières se placent de façon privilégiée sur les lignes de gradient élevé.

Plusieurs algorithmes de calcul de ligne de partage des eaux ont une complexité linéaire en fonction du nombre de pixels de l'image, ce qui les place parmi les méthodes de segmentation les plus rapides.

À l’origine la morphologie mathématique a été conçue pour traiter et analyser des images de matériaux ou images biologiques afin d’en extraire des informations quantifiées sous forme de paramètres ou de fonctions:. Ici, on se limitera aux images 2D définies dans l’espace ${\displaystyle E=\mathbb {Z} ^{2}}$ et aux sous-espaces. Dans ce cas l’espace ${\displaystyle \mathbb {Z} ^{2}}$ est représenté par une grille de points. Deux cas sont envisagés: la grille carrée (pavage carré) et la grille triangulaire (pavage hexagonal). En ce qui concerne les paramètres, on sait qu’ils peuvent être obtenus à partir de la caractéristique d’Euler-Poincaré ou nombre de connexité des différents espaces, notés ${\displaystyle N_{n}(X)}$ pour l’espace ${\displaystyle \mathbb {R} ^{n}}$.

• 
  Pavage carré d'un ensemble X
• 
  Ensemble X et configuration de voisinage pour obtenir N1 (pavage carré)
• 
  Ensemble X et configurations de voisinage pour obtenir N2 (pavage carré)

Cet espace correspond au réseau de points associés aux pixels.Sur l’image binaire, ${\displaystyle N_{0}(X)}$ est égal au nombre de pixel à 1.

Les droites ${\displaystyle \Delta }$ utilisables dans ${\displaystyle \mathbb {Z} ^{2}}$ correspondent à des pixels alignés. Les extrémités de segments de ces droites coupant ${\displaystyle X}$ correspondent (en sortie) à des transitions de pixel de type 1 0. L’image binaire associée ${\displaystyle Y}$ est obtenue par une transformation en tout ou rien. D'un point de vue pratique cela revient à vérifier, pour chaque pixel ${\displaystyle x}$, la configuration de voisinage ${\displaystyle T(x)}$. Les éléments 1 de la configuration sont relatifs à l’ensemble ${\displaystyle X}$ et ceux à 0 au complémentaire. On aura donc :Pour l'ensemble : ${\displaystyle Y=\eta _{T}(X)}$Pour la mesure : ${\displaystyle N_{1}(X)=N_{0}(Y)}$

Les éléments structurants dans les différents pavages sont :

• En pavage hexagonal dans la direction 0 : ${\displaystyle T(x)={\begin{bmatrix}&.&&.&\\.&&1&&0\\&.&&.&\end{bmatrix}}}$.

(Les autres orientations à 60° et 120° sont obtenues par rotation de la configuration.)

• En pavage carré dans la direction 0 : ${\displaystyle T(x)={\begin{bmatrix}.&&.&&.\\.&&1&&0\\.&&.&&.\end{bmatrix}}}$.

(Les autres orientations à 45°, 90°, 135° sont obtenues par rotation de la configuration.)

Rappelons que ${\displaystyle N_{2}(X)}$ correspond au nombre de composantes connexes diminué du nombre de trous qu’elles contiennent.

• Pavage hexagonal

Pour déterminer ce nombre avec le pavage triangulaire, on utilise la relation d’Euler : ${\displaystyle \chi =N_{2}(X)=s-c-f}$En pavage hexagonal s représentant le nombre de sommets (pixels à 1), c le nombre de côtés de type 1-1 (à une rotation près) et f le nombre de triangles ayant les 3 sommets à 1. Un calcul élémentaire sur toutes les combinaisons donne le résultat suivant :Pour les ensembles : ${\displaystyle Y1=\eta _{T1}(X)}$ et ${\displaystyle Y2=\eta _{T2}(X)}$Pour la mesure : ${\displaystyle N_{2}(X)=N_{0}(Y1)-N_{0}(Y2)}$

Les éléments structurants dans les différents pavages sont :

${\displaystyle T1(x)={\begin{bmatrix}&.&&0&\\.&&1&&0\\&.&&.&\end{bmatrix}}}$ et ${\displaystyle T2(x)={\begin{bmatrix}&1&&0&\\.&&1&&.\\&.&&.&\end{bmatrix}}}$.

• En pavage carré (8 connexité) on fait le même raisonnement ce qui donne les éléments structurants :

${\displaystyle T1(x)={\begin{bmatrix}.&&.&&.\\.&&1&&0\\.&&0&&0\end{bmatrix}}}$ et ${\displaystyle T2(x)={\begin{bmatrix}.&&.&&.\\.&&.&&1\\.&&1&&0\end{bmatrix}}}$.

Comme pour les nombres de connexité, les paramètres métriques de base doivent vérifier les conditions de Hugo Hadwiger. L’ensemble ${\displaystyle {X}}$ doit être un ensemble aléatoire stationnaire et constitué d’une union finie de convexes. La mesure ${\displaystyle W}$ doit avoir les propriétés suivantes :

• Invariante par translation de ${\displaystyle {\vec {t}}}$ :${\displaystyle {W(X)=W({X_{\vec {t}})}}}$
• Compatible avec homothéties (agrandissement ${\displaystyle \lambda }$) :${\displaystyle {W(X)={\frac {W({\lambda }X)}{\lambda ^{k}}}}}$
• C-additive :${\displaystyle {W(X)+W(Y)=W(X\cup Y)+W(X\cap Y)}}$
• Continue ou semi continue

Le paramètre métrique est la longueur totale de l’ensemble ${\displaystyle X}$ notée ${\displaystyle L_{1}(X)}$.Elle se calcule à partir de ${\displaystyle N_{0}(X)}$ et la taille du pixel ${\displaystyle \mathrm {d} D}$. On a en effet :${\displaystyle {L_{1}}(X)=N_{0}(X)\times \mathrm {d} D}$

Ces paramètres métriques sont:

• L’aire de l’ensemble ${\displaystyle X}$ notée ${\displaystyle A(X)}$

Elle se calcule à partir de ${\displaystyle N_{0}(X)}$ et l’aire du pixel ${\displaystyle \mathrm {d} A}$. On a en effet : ${\displaystyle {A}(X)=N_{0}(X)\times \mathrm {d} A}$

• Le périmètre de l’ensemble ${\displaystyle X}$ noté ${\displaystyle L_{2}(X)}$

Pour obtenir ce périmètre, on va utiliser la relation de Cauchy (géométrie intégrale) qui relie la variation diamétrale d'un ensemble à son périmètre :${\displaystyle L_{2}(X)=\int _{0}^{\pi }D_{2}(X,\alpha )\times \mathrm {d} \alpha =\pi \times \mathbb {E} [{D(X)}]=\pi \times \mathbb {E} [{N_{1}(X)}]\times \mathrm {d} D}$ avec ${\displaystyle \mathrm {d} D}$ taille du pixel. On notera que l'estimation de ce périmètre à un aspect statistique. Le nombre de connexité ${\displaystyle N_{1}(X,\alpha )}$ doit être estimé dans plusieurs directions.

• 
  Illustration de la relation de Cauchy
• 
  Illustration de la relation de Crofton
• 
  Illustration de la relation de Meunier

La géométrie intégrale permet également d’accéder à des paramètres de ${\displaystyle \mathbb {R} ^{3}}$ en utilisant les nombres de connexité des espaces inférieures.

• Ainsi, la surface de la frontière ${\displaystyle \partial X}$ notée ${\displaystyle S(X)}$ est obtenue à partir du nombre de connexité ${\displaystyle N_{1}(X)}$ par la relation de Crofton :${\displaystyle S(X)={\frac {1}{\pi }}\int _{0}^{4\pi }A(X',\omega )\times \mathrm {d} \omega =4\times \mathbb {E} [A(X')]=4\times \mathbb {E} [{N_{1}(X)}]\times \mathrm {d} A}$${\displaystyle X'}$ est la projection de ${\displaystyle X}$ sur le plan ${\displaystyle \Pi }$ perpendiculaire à la direction ${\displaystyle \omega }$ et ${\displaystyle \mathrm {d} A}$ l'aire associée à la ligne ${\displaystyle \Delta }$.

• L'intégrale de courbure moyenne est estimée à partir de la variation diamétrale dans ${\displaystyle {\mathbb {R} ^{3}}}$ notée ${\displaystyle D_{3}(X,\omega )}$en utilisant la relation de Meusnier:${\displaystyle M(X)=2\pi \times {\mathbb {E} [D_{3}(X,\omega )]}}$Cette variation diamétrale est reliée au nombre de connexité dans ${\displaystyle {\mathbb {R} ^{2}}}$ par la relation :${\displaystyle D_{3}(X,\omega )=N_{2}(X,\omega )\times \mathrm {d} D_{3}}$Ce qui donne finalement :${\displaystyle M(X)=2\pi \times {\mathbb {E} [N_{2}(X,\omega )]\times \mathrm {d} D_{3}}}$${\displaystyle \mathrm {d} D_{3}}$ représente la distance entre 2 plans.

Les images destinées aux études scientifiques sont souvent obtenues à partir d’un microscope dont le champ est plus petit que l’ensemble à analyser. Dans ce cas, on dit que l’analyse est locale par opposition à l’analyse globale où l’ensemble est totalement visible.

Les paramètres globaux précédemment définis doivent être transformés en paramètres locaux ramenés à l’unité d’espace.

• L’unique paramètre est la fraction de points :${\displaystyle {N_{P}(X)={\frac {N_{0}(X\cap Z_{0})}{N_{0}(Z_{0})}}}}$

• Fraction linéique :${\displaystyle {L_{L}(X)={\frac {L_{1}(X\cap Z_{1})}{L(Z_{1})}}}}$Dans ce contexte statistique, on démontre aisément que l'estimation de la fraction linéique est égale à la fraction de points :${\displaystyle {L_{L}(X)=N_{P}(X)}}$

• Nombre de connexité par unité de longueur:${\displaystyle {N_{L}(X)={\frac {N_{1}(X\cap Z_{1})}{L(Z_{1})}}}}$

• Fraction surfacique :${\displaystyle {A_{A}(X)={\frac {A(X\cap Z_{2})}{A(Z_{2})}}}}$On a également :${\displaystyle {A_{A}(X)=N_{P}(X)}}$

• Périmètre spécifique :${\displaystyle {L_{A}(X)={\frac {L_{2}(X\cap Z_{2})}{A(Z_{2})}}}}$En utilisant la relation de Cauchy, on obtient :${\displaystyle {L_{A}(X)=\pi \times N_{L}(X)}}$

• Nombre de connexité par unité de surface :${\displaystyle {N_{A}(X)={\frac {N_{2}(X\cap Z_{2})}{A(Z_{2})}}}}$

• Fraction volumique :${\displaystyle {V_{V}(X)={\frac {V(X\cap Z_{3})}{V(Z_{3})}}}}$Ici encore, on a :${\displaystyle {V_{V}(X)=N_{P}(X)}}$

• Surface spécifique :${\displaystyle {S_{V}(X)={\frac {S(X\cap Z_{3})}{V(Z_{3})}}}}$En utilisant la relation de Crofton, on a :${\displaystyle {S_{V}(X)=4\times N_{L}(X)}}$

• Intégrale de courbure moyenne par unité de volume :${\displaystyle {M_{V}(X)={\frac {M_{3}(X\cap Z_{3})}{V(Z_{3})}}}}$L'intégrale de courbure moyenne peut être estimée à partir du nombre de connexité dans ${\displaystyle {\mathbb {R} ^{2}}}$ selon la relation de Meusnier :${\displaystyle {M_{V}(X)=2\pi \times N_{A}(X)}}$

• Nombre de connexité par unité de volume :${\displaystyle {N_{V}(X)={\frac {N_{3}(X\cap Z_{3})}{V(Z_{3})}}}}$Ce paramètre de nature topologique n'est pas accessible à partir des espaces de dimension inférieure.

Les paramètres stéréologiques sont des paramètres moyens. De plus, ils ne sont pas nombreux. On conçoit aisément qu’ils soient insuffisants pour donner une description assez complète de la structure. Si l’on accepte de perdre l’aspect stéréologique, la morphologie mathématique permet d’obtenir de nombreuses informations quantitatives supplémentaires. Cette quantification dépend souvent d’un paramètre de taille ${\displaystyle \lambda }$ associé aux transformations d’images. La quantification conduira à une opération de tri ${\displaystyle \Psi _{\lambda }(X)}$ dont le dénombrement ou la mesure conduira à une fonction granulométrique. La dispersion d’un ensemble dans un autre est également quelque chose d’important à connaître. La stéréologie ne fournit qu’un paramètre dérivé qui est loin de répondre à la question.

La méthode de tri doit vérifier les règles suivantes :

• La méthode de tri doit vérifier la propriété de croissance${\displaystyle X\subset Y\Rightarrow \Psi _{\lambda }(X)\subset \Psi _{\lambda }(Y)}$
• La méthode de tri est anti-extensive${\displaystyle \Psi _{\lambda }(X)\subset X}$

• Dans le cas de deux tris successifs, c’est le paramètre le plus grand qui l’emporte. Le résultat est indépendant de l’ordre des opérateurs. Cela s’écrit :${\displaystyle \Psi _{\lambda 2}(\Psi _{\lambda 1}(X))=\Psi _{\lambda 1}(\Psi _{\lambda 2}(X))=\Psi _{sup(\lambda 2,\lambda 1)}(X)}$ Cette dernière condition va réduire considérablement le nombre des opérateurs candidats.

On distingue les granulométries en nombre et les granulométries en mesure.

• Si le tri granulométrique ${\displaystyle \Psi _{\lambda }(X)}$ consiste à ne conserver que tout ce qui est plus petit que ${\displaystyle \lambda }$, alors la fonction de distribution granulométrique en nombre sera définie par :${\displaystyle F(X,\lambda )={\frac {Nb(X)-Nb(\Psi _{\lambda }(X))}{Nb(X)}}}$

• Au lieu de compter les objets, on peut reporter une mesure qui leur est associée (la masse dans un tamis).On obtient alors une fonction de distribution granulométrique en mesure définie par :${\displaystyle G(X,\lambda )={\frac {Mes(X)-Mes(\Psi _{\lambda }(X))}{Mes(X)}}}$ En analyse d’image la mesure est le volume dans ${\displaystyle \mathbb {R} ^{3}}$, l’aire pour ${\displaystyle \mathbb {R} ^{2}}$ et la longueur pour ${\displaystyle \mathbb {R} ^{1}}$.

Ce type d’analyse n’est possible que si l’ensemble à analyser est constitué d’une collection d’objets totalement disjoints. Chaque objet est isolé puis mesuré selon un critère de taille (aire, périmètre diamètre de Féret…). Le résultat de la mesure permet de mettre cet objet dans une classe de taille.

• Les problèmes du masque de mesure

Pour faire les mesures qu’on vient de citer, il est nécessaire que l’objet soit totalement inclus dans le champ de mesures. On doit donc éliminer ceux qui coupent le bord du champ. On a vu que cela est facilement réalisé par morphologie mathématique . Cependant, on a d’autant plus de chance d’éliminer un objet que sa taille est grande. Cela va introduire un biais dans l’analyse granulométrique. Pour résoudre ce problème, il faut pouvoir connaître la probabilité qu’un objet ${\displaystyle X_{i}}$ a d’être inclus dans le champ ${\displaystyle Z}$. Or, on a vu que ${\displaystyle \epsilon _{B}(X)}$ donne l’ensemble des points de ${\displaystyle X}$ où ${\displaystyle B}$ est totalement inclus dans ${\displaystyle X}$.

Ce raisonnement peut être transcrit pour résoudre notre problème en cherchant à éroder le masque rectangulaire ${\displaystyle Z}$ par ${\displaystyle X_{i}}$. Il est facile de voir qu’on obtiendra rigoureusement le même résultat si on remplace ${\displaystyle X_{i}}$ par le rectangle circonscrit minimum ${\displaystyle R_{i}}$ de même orientation que ${\displaystyle Z}$. La probabilité d’inclusion ${\displaystyle \Pr(X)}$ se calcule alors facilement : ${\displaystyle \Pr(X_{i})={\frac {A(\epsilon _{R_{i}}(Z))}{A(Z)}}={\frac {(a_{Z}-a_{R})\times (b_{Z}-b_{R})}{a_{Z}\times b_{Z}}}}$ Dans cette expression, ${\displaystyle a}$ représente le côté horizontal et ${\displaystyle b}$ le côté vertical du champ (indice Z) ou du rectangle (indice R). Le biais sera alors corrigé en incrémentant la classe de taille non pas de 1 mais de ${\displaystyle 1/\Pr(X_{i})}$. Cette méthode corrective a été proposée par Lantuéjoul.

Le milieu complémentaire des objets de la figure 1 ne peut pas être traité par cette méthode car la notion d’objet individuel n’a plus de sens. Cependant les axiomes de Matheron se vérifient lorsque l’ouverture est faite avec un élément structurant convexe. En effet, un élément structurant convexe permet de construire une famille de même nature dont tous les membres se déduisent de l’élément de taille 1 par un rapport d’homothétie de taille ${\displaystyle \lambda }$. Ce type de granulométrie est une granulométrie en mesure car l’ouverture ne possède pas de bonnes propriétés topologiques (un objet peut être scindé en deux par ouverture). Pour une image définie dans ${\displaystyle \mathbb {R} ^{2}}$, la seule mesure utilisée est l’aire de l’ensemble ouvert.

• 
  Ensemble Booléen de disques circulaires (X= BD)
• 
  Ouverture hexagonale de taille 5 pixels sur BD et masque érodé (cyan)
• 
  Ouverture hexagonale de taille 20 pixels sur BD et masque érodé (cyan)

En analyse locale, il faut tenir compte du masque de mesure et donc travailler dans un masque érodé, on a donc : ${\displaystyle G(X,\lambda B)={\frac {A_{A}(X\cap \epsilon _{2\lambda B}(Z))-A_{A}(\gamma _{\lambda B}(X)\cap \epsilon _{2\lambda B}(Z))}{A_{A}(X\cap \epsilon _{2\lambda B}(Z)}}}$ Il existe un cas particulier où la granulométrie peut être établie en nombre. C’est lorsque l’ensemble ${\displaystyle {\hat {X}}}$ est constitué d’objets convexes disjoints. Dans ce cas, on aura : ${\displaystyle F({\hat {X}},\lambda B)={\frac {N_{A}({\hat {X}}\cap \epsilon _{2\lambda B}(Z))-N_{A}(\gamma _{\lambda B}({\hat {X}})\cap \epsilon _{2\lambda B}(Z))}{N_{A}({\hat {X}}\cap \epsilon _{2\lambda B}(Z)}}}$

L’élément structurant linéaire est traditionnellement noté ${\displaystyle \ell }$. Les règles s’appliquent de la même manière que pour l’ouverture bidimensionnelle mais ici les granulométries en mesure et en nombre peuvent toujours se calculer puisque l’intersection d’un ensemble ${\displaystyle X}$ par une droite