Table d'ombre — Wikipédia
Une table d'ombre est un tableau qui donne approximativement la longueur de l'ombre d'un « gnomon » en fonction d'un « mois » de l'année et de l'« heure » du jour.

De différentes factures, ces tables qui donnent grossièrement l'heure ont leur origine et leur premier usage dans l'Antiquité. On les retrouvera plus tard, dans le haut Moyen Âge, dans les communautés religieuses chrétiennes ; elles serviront alors momentanément d'indicateur temps dans la mise en application supposée des règles monastiques.
Plus tard elles seront remplacées par des instruments plus pratiques tels les cadrans canoniaux suivis chronologiquement par les horloges hydrauliques puis mécaniques.
Exemple
[modifier | modifier le code]On s'appuiera sur la table d'un pseudo-Bède[1] supposé être du XIIe siècle, décrite par Jean-Baptiste Delambre[2].

Description
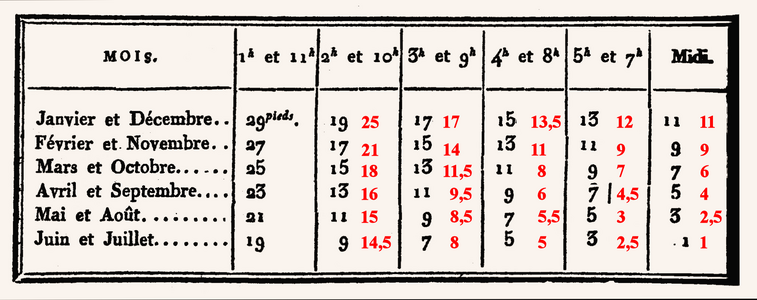
[modifier | modifier le code]On trouvera dans ce tableau :
- une première colonne définissant le champ des mois ;
- six colonnes correspondant aux champs des différentes heures ;
- pour chaque ligne, dans les colonnes des heures, les valeurs successives des longueurs d'ombre en lien avec les mois considérés.
- les mois
Ici, ils sont donnés par deux pour simplifier la table. Leur regroupement suit grossièrement l'évolution de la déclinaison du Soleil dans l'année ; ainsi le milieu des mois Janvier et Décembre correspond à peu près aux ombres les plus longues du solstice d'hiver, le milieu de Juin et Juillet, lui correspond à l'ombre la plus courte au solstice d'été, quant aux équinoxes, vers le milieu de Mars et Septembre, ils sont plus grossièrement distribués dans les mois Mars et Octobre et Avril et Septembre. D'autres tables, par ailleurs, plus en liaison avec la course du Soleil donnent des « mois » zodiacaux.
- les heures
Ce sont toujours des heures temporaires, les seules en usage « grand public » dans l'Antiquité et au Moyen Âge « jusqu'à l'époque où chaque ville et chaque village a eu son horloge à roues. ». Ici, les heures temporaires sont désignées de façon conventionnelle (de la deuxième heure solaire à la onzième avec origine au lever du Soleil), l'heure de midi correspondant à la sixième heure temporaire.
- les longueurs d'ombre
Le « gnomon » est ici le corps humain ; chaque longueur d'ombre - sous-entendu sur un sol horizontal - est exprimée en valeurs arrondies de pieds, pieds de celui qui mesure la grandeur de son ombre[N 1]. Ainsi chacun peut-il savoir l'heure sans matériel particulier. Le corps humain semble être la règle pour matérialiser un gnomon quelle que soit la table examinée.
Remarques :
« D'un mois au suivant, toutes les différences sont de deux pieds, à l'exception d'une seule probablement due à une faute d'impression corrigée [par Delambre] », qui souligne : « comme tout cela doit être exact. »
Ces différences de deux pieds se retrouvent aussi entre colonnes, à l'exception de celles concernant la colonne 1h et 11 h et la suivante.
Toujours d'après Delambre, « l'auteur de la table a oublié de marquer pour quelle latitude il a calculé ses ombres. »

Approche gnomonique succincte
[modifier | modifier le code]En gnomonique, la longueur x de l'ombre d'un gnomon au cours de la journée est donnée à partir de la hauteur h du Soleil :
où Φ est la latitude, δ la déclinaison du Soleil et H l'angle horaire du Soleil exprimé en degrés (en gnomonique on compte H à raison de 15° par heure solaire vraie : midi = 0°, 13 h = 15°, 14 h = 30°, 11 h = -15°, 10 h = -30°, etc.) ; on constate ici que la hauteur du Soleil est tributaire de la latitude du lieu.
À midi, la formule se simplifie et on a :
La longueur de l'ombre x, elle est fonction de la longueur du gnomon L et de la hauteur du Soleil :
On peut, à partir de ces formules[3], calculer la latitude approchée du lieu où s'applique la table : Tout d'abord, en prenant l'hypothèse que le rapport de la longueur du pied à la taille d'un individu est de 15 % (voir note 1) on a la longueur du gnomon L = 1 / 0,15 = 6,66 pieds, quel que soit l'individu.
- Aux solstices, à midi, en prenant une longueur d'ombre de 11 pieds pour l'hiver et de 1 pied pour l'été, avec une déclinaison de ± 24 °, valeur entière conventionnelle employée dans l'Antiquité, on trouverait :
Pour l'hiver : de [3] on tire h1m = 33,18°, valeur qui reportée dans [2] donne Φ1 = 32,8°.
Pour l'été... : de [3] on tire h2m = 81,46°, valeur qui reportée dans [2] donne Φ2 = 32,5°.
Ces valeurs calculées correspondent à une latitude nord-africaine inférieure à celle de Casablanca, 33,65° et de Carthage, 36,85° mais supérieure à celle d'Alexandrie, 31,2°.
- En prenant une latitude de 32,5° à priori, aux équinoxes (δ = 0), à midi, hm = 57,5° d'où une longueur d'ombre de l'ordre de 4,25 pieds, ce qui ne correspond guère aux valeurs 5 et 7 de la table données pour les mois d'équinoxe.
À titre indicatif on peut construire une table d'ombre contemporaine en heures solaires vraies à partir de la formule [1]. On peut aussi retrouver les longueurs de l'ombre d'un gnomon en fonction des heures temporaires : On propose ici une méthode graphique simple qui s'appuie sur le tracé des cadrans solaires : Sur la figure d'un cadran solaire horizontal pour une latitude de 32,5°, à style droit et heures temporaires (contemporaines)[4] on peut constater :
- d'une part que le regroupement en mois de la table est judicieux (J-D, F-N, M-O, A-S, M-A, J-J) dans un souci de simplification mais avec un intervalle de variation plus important vers les mois d'équinoxes ;
- d'autre part que la mesure des longueurs d'ombre est immédiate en se donnant une longueur de pied choisie : ici la longueur du pied est donnée à partir de la mesure de la longueur de l'ombre entre A, pied du gnomon et le point maximum de l'ombre à midi au solstice d'hiver (11 pieds)[N 2]. Ces mesures peuvent être rapportées dans le tableau précédent. Comparées aux valeurs initiales données par la table, on peut constater des écarts très disparates non exploitables entre les deux types d'informations.
- Table pour une latitude de 32,5°
- Cadran à heures temporaires.
- Table de comparaison des longueurs d'ombre (en rouge, valeurs "vraies").
D'autres méthodes algébriques permettent de calculer les longueurs de l'ombre d'un gnomon en fonction des heures temporaires ; elles ne sont pas proposées ici[5].
En conclusion, on insistera encore sur le fait que ces tables étaient très approximatives dans leurs données. Elles ne permettaient donc pas de connaitre le temps avec exactitude. Dans un usage quotidien, les communautés s'accommodaient de ces imprécisions transparentes qui n'entravaient en rien leurs règles de vie.
Histoire
[modifier | modifier le code]La variation de la longueur de l'ombre d'un gnomon en fonction de l'« heure » de la journée semble avoir être constatée en Égypte depuis la haute Antiquité. D'après Borchardt, cité par Jérôme Bonnin[6], il existerait une table d'ombre primitive datée du Moyen Empire (avant l'an -1786).
Plus près de nous, à l' époque hellénistique, dès le IVe siècle avant notre ère, des textes de comédies grecques font mention de la mesure de sa propre ombre pour arriver à l'heure aux repas[7].
En Grèce, la plus ancienne table d'ombre reconnue comme telle, est datée de -200[9]. Dès cette époque, l'apparition des tables d'ombre semble coïncider avec le développement des cadrans solaires. Elles sont dressées en fonction des saisons et sont liées aux heures du jour. Les premières tables semblent organisées autour des signes du zodiaque, puis des mois de l'année. La longueur de l'ombre est exprimée en pas, puis en pieds de l'utilisateur, donnant un peu plus de régularité dans les mesures.
Les Romains les reproduiront, et ce, jusqu'à l'époque médiévale[10]. Sur ces tables, aucune mention de latitude, information fondamentale pour leur construction. En voici quelques exemples, dans un ordre chronologique.
Table de Palladius ( IVe siècle)
[modifier | modifier le code]Dans son Traité d'agriculture (371 - 395), Palladius donne à la fin de chaque chapitre consacré à un mois de l'année une table d'ombre partielle[11]. La compilation sur l'année est donnée ici dans l'introduction ; les longueurs d'ombre sont en pieds.

On peut constater que, par souci de simplification et peut-être pour une meilleure mémorisation partielle, les valeurs indiquées sont données arrondies à l'unité avec une progression entre les heures identique (1, 2, 3, 4, 10) quel que soit le mois considéré. Ces valeurs se trouvent dans la dernière colonne « Différences » du tableau ; non indiquée sur ce dernier, la différence pour une même heure entre deux mois consécutifs (1, 1, 1, 2, 2 de juillet à décembre par exemple). Ce souci de simplification que l'on retrouve sur toutes les tables présentées fait que l'exactitude s'en ressent, comme on a pu le constater précédemment.
Palladius possédait des terres vers Naples qui ont peut-être servi de référence à son traité d'agriculture. La latitude de Naples est de 40,83°, latitude ne correspondant pas à sa table d'ombre.
Table de Taphis ( Ve siècle)
[modifier | modifier le code]

Taphis, aujourd'hui Tafa, est un village nubien de latitude 23,66° situé près d'Assouan en Égypte. On y trouve un petit édifice d'époque romaine, transformé en église au Ve siècle, le temple de Tafa. De chaque côté de la porte du naos, on trouve une inscription grecque qui s'avère être une table d'ombre[12].
Le fac-simile partiel de l'inscription grecque de gauche laisse apparaitre dans sa partie haute les noms de plusieurs mois du calendrier alexandrin en usage en Égypte au (Ve siècle), ΦΑMENωC, MEXI , TVII, XOIAK, soit Phamenoth, Méchir, Tybi, Chæack ; dessous, des colonnes de chiffres. Transcrites, ces inscriptions ont permis de reconstituer la table d'ombre pour six mois telle que proposée par l'auteur de l'article. Les manques ont été reconstitués à partir des progressions constatées entre les valeurs décryptées du fac-simile.

L'étude se poursuit avec une comparaison entre la table de Taphis et celle de Palladius, permettant de constater leur facture équivalente ainsi que leur « imprécision ».

Table d'Ammaedara (vers 650-700)
[modifier | modifier le code]Le site archéologique de Haïdra, l'antique Ammaedara se trouve au centre-ouest du gouvernorat de Kasserine, situé à Haïdra en Tunisie. La latitude du lieu est de 35,57°.
Des travaux entrepris depuis 1993 ont permis de découvrir sur le site les vestiges d'une table d'ombre près d'une petite église : quelques fragments dispersés ont permis de reconstituer la table dans son ensemble. Elle s'intègre bien dans l'ensemble des autres tables décrites précédemment. Sa présentation détaillée fait l'objet d'un article actuel bien documenté dans les Comptes rendus des séances de l'Académie des Inscriptions et Belles-Lettres de 2004[13].
Sur le tableau présenté ci-dessous on voit bien les éléments encadrés en bleu qui ont permis la reconstitution de la table, suivant des règles détaillés plus haut.

Tables arabes
[modifier | modifier le code]Les tables d'ombre étaient connues de la civilisation arabe. Leur description et leur histoire ont été abordées par David A. King[14].
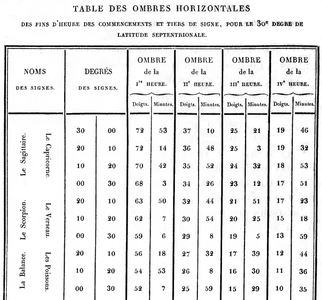
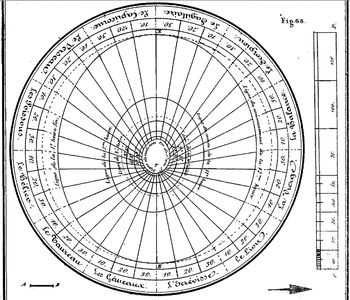
On peut citer, parmi les auteurs, Abū al-Ḥasan'Alī Marrākushī dit aussi Aboul-Hhassan qui donna au Caire au XIIIe siècle un ensemble de tables d'ombre pour des cadrans horizontaux, verticaux, cylindriques[15]. Ces tables, calculées, avaient un usage gnomonique, contrairement aux tables décrites précédemment qui étaient d'usage public[16]. Les longueurs d'ombre des tables, toujours pour les heures temporaires, ont été représentées par l'auteur sur une figure ayant la forme d'un disque qu'il dénomme sabot[17].
- Une table d'ombre d'Aboul-Hhassan, XIIIe siècle
- Table partielle : les longueurs d'ombre des heures sont données de 10° en 10° sur le zodiaque.
- Le sabot, image de la table ; le gnomon AB est planté au centre des ovales en T.
Notes et références
[modifier | modifier le code]Notes
[modifier | modifier le code]- ↑ Il existe une corrélation évidente, mise en application ici, entre la taille d'un individu (hauteur de gnomon) et la longueur de son pied (unité de mesure de l'ombre). Pour information, le rapport L pied / Taille = ± 15 %.
- ↑ Une autre longueur d'ombre est représentée par le vecteur A-10 = 14,5 pieds ; elle correspond à la longueur d'ombre de la dixième heure des mois de juin-juillet soit à la valeur 9 de la table.
Références
[modifier | modifier le code]- ↑ Delambre attribue à Bède, par erreur, l'ouvrage désigné ci-après de Mundi coelestis terristrisque constitutione où se trouve une table d'ombre ; voir l'attribution à un pseudo-Bède dans Die Sangspruchdichtung Rumelants von Sachsen- référence en ligne
- ↑ Jean-Baptiste Delambre 1817
- ↑ Denis Savoie, Les cadrans solaires, Paris, Belin, pour la science, , 127 p. (ISBN 2-7011-3338-6), p. 41 ; 111-12 ; 118-119.
- ↑ Tracé exécuté à partir du logiciel Shadows
- ↑ Voir : Denis Savoie, La gnomonique : Chap. XXI Cadrans solaires d'heures temporaires, Paris, Les Belles Lettres, , 521 p. (ISBN 978-2-251-42030-1), p. 295-301.
- ↑ Jérôme Bonnin 2015, p. 35, note 3.
- ↑ Jérôme Bonnin 2015, p. 35, note 4.
- ↑ Texte d'Aristophane, cité par Jérôme Bonnin ; d'autres citations d'Eubule et Ménandre font appel à la même notion.
- ↑ D'après R. Hannah cité par Jérôme Bonnin, p. 35.
- ↑ Jérôme Bonnin 2015, p. 36.
- ↑ Jérôme Bonnin 2015, p. 36, note 3.
- ↑ MM. J. B. Eyriès et Malte-Brun, Nouvelles annales des voyages, de la géographie et de l'histoire : Mémoire sur une table horaire, t. XVII, (lire en ligne), p. 357-383 ; autre référence de l'ouvrage, Google books : accès en ligne
- ↑ Baratte François et Bejaoui Fathi, Comptes rendus des séances de l'Académie des Inscriptions et Belles-Lettres : Un évêque horloger dans l'Afrique byzantine : Hyacinthe d'Ammaedara, vol. 3, (lire en ligne), p. 1121-1151.
- ↑ David A. King, Histoire des sciences arabes : Astronomie et société musulmane, Paris, R. Rashed au Seuil, , p. 173-215.
- ↑ Denis Savoie, L'âge d'or des sciences arabes : Les cadrans solaires arabo-islamiques, Paris, Actes Sud, (ISBN 2-7427-5672-8), p. 113.
- ↑ J.-J. Sédillot, Traité des instruments astronomiques des Arabes, Paris, L.-AM. Sédillot, (lire en ligne), p. 423 et pl. VI, p. 656.
- ↑ L'ouvrage de Sédillot a été analysé par Jean-Baptiste Delambre, Histoire de l'astronomie du Moyen Âge, Paris, (lire en ligne), p. 515.
Annexes
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
 Jean-Baptiste Delambre, Histoire de l'Astronomie ancienne, t. I, Paris, Coursier, (lire en ligne), p. 321-324.
Jean-Baptiste Delambre, Histoire de l'Astronomie ancienne, t. I, Paris, Coursier, (lire en ligne), p. 321-324. Denis Savoie, Les cadrans solaires, Paris, Belin, pour la science, , 127 p. (ISBN 2-7011-3338-6).
Denis Savoie, Les cadrans solaires, Paris, Belin, pour la science, , 127 p. (ISBN 2-7011-3338-6). Denis Savoie, La gnomonique : Chap. XXI Cadrans solaires d'heures temporaires, Paris, Les Belles Lettres, , 521 p. (ISBN 978-2-251-42030-1), p. 295-301.
Denis Savoie, La gnomonique : Chap. XXI Cadrans solaires d'heures temporaires, Paris, Les Belles Lettres, , 521 p. (ISBN 978-2-251-42030-1), p. 295-301. Jérôme Bonnin, La mesure du temps dans l'Antiquité, Paris, Les Belles Lettres, , 444 p. (ISBN 978-2-251-44509-0).
Jérôme Bonnin, La mesure du temps dans l'Antiquité, Paris, Les Belles Lettres, , 444 p. (ISBN 978-2-251-44509-0).
Articles connexes
[modifier | modifier le code]Liens externes
[modifier | modifier le code]- Article de Michel Lalos sur les tables d'ombre : accès en ligne


 French
French Deutsch
Deutsch