マルコフ決定過程

マルコフ決定過程（マルコフけっていかてい、英: Markov decision process; MDP）は、状態遷移が確率的に生じる動的システム（確率システム）の確率モデルであり、状態遷移がマルコフ性を満たすものをいう。 MDP は不確実性を伴う意思決定のモデリングにおける数学的枠組みとして、強化学習など動的計画法が適用される幅広い最適化問題の研究に活用されている。 MDP は少なくとも1950年代には知られていた^[1]が、研究の中核は1960年に出版された Ronald A. Howard の "Dynamic Programming and Markov Processes" に起因する^[2]。 MDP はロボット工学や自動制御、経済学、製造業を含む幅広い分野で用いられている。

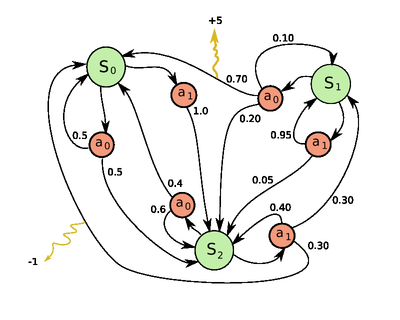
マルコフ決定過程は離散時間における確率制御過程 (stochastic control process) である。 各時刻において過程 (process) はある状態 (state) を取り、意思決定者 (decision maker) はその状態において利用可能な行動 (action) を任意に選択する。 その後過程はランダムに新しい状態へと遷移し、その際に意思決定者は状態遷移に対応した報酬 (reward) を受けとる。

遷移後の状態 ${\displaystyle s'}$ 、および得られる報酬の値 ${\displaystyle r}$ は現在の状態 ${\displaystyle s}$ と行動 ${\displaystyle a}$ のみに依存し、${\displaystyle s}$ と ${\displaystyle a}$ が与えられたもとでそれより過去の状態および行動と条件付き独立となる。 言い換えると、マルコフ決定過程の状態遷移はマルコフ性を満たす。

マルコフ決定過程はマルコフ連鎖に（選択可能な）行動、および（行動を計画する動機を与える）報酬を追加し拡張したものであると解釈できる。 逆に言えば、各ステップにとる行動がそのステップにおける状態のみ依存するとき、マルコフ決定過程は等価なマルコフ連鎖に置き換えることが出来る。

MDP は4つの要素の組 ${\textstyle (S,A,T,R)}$で表される。ここで各要素はそれぞれ次を意味する。

• ${\displaystyle S}$ は状態の集合であり、状態空間 (state space) と呼ばれる。
• ${\displaystyle A}$ は行動の集合であり、行動空間 (action space) と呼ばれる。特に、ある特定の状態 ${\displaystyle s\in S}$ で取ることの出来る行動の集合を ${\displaystyle A_{s}\subset A}$ によって表記する。
• ${\displaystyle T}$ は遷移関数 (transition function) と呼ばれ、状態 ${\displaystyle s\in S}$ において行動 ${\displaystyle a\in A_{s}}$ を取った場合における状態 ${\displaystyle s'\in S}$ への状態遷移確率を規定する実数値 ${\displaystyle T(s,a,s')\in [0,1]}$ を割り当てる。
• ${\displaystyle R}$ は報酬関数 (reward function) と呼ばれ、状態 ${\displaystyle s\in S}$ から ${\displaystyle s'\in S}$ に行動 ${\displaystyle a\in A_{s}}$ を伴い遷移することによって得られる即時報酬 (immediate reward) またはその期待値を表わす実数値 ${\displaystyle R(s,a,s')\in \mathbb {R} }$ を規定する。

状態空間 ${\displaystyle S}$ および行動空間 ${\displaystyle A}$ は、有限集合の場合と（実数値すべての集合のような）無限集合の場合がある。特に ${\displaystyle S}$ と ${\displaystyle A}$ がともに有限集合であるような MDP は有限マルコフ決定過程 (finite Markov decision process; finite MDP) と呼ばれる。状態空間が有限である場合においては、時刻 ${\displaystyle t}$ における状態遷移確率は遷移関数によって $${\displaystyle \Pr(s_{t+1}=s'\mid s_{t}=s,a_{t}=a)=T(s,a,s')}$$ と記述することが出来る。 （状態空間が有限でない）より一般的なケースにおいては、任意の可測集合 ${\displaystyle S'\subset S}$ に対して状態遷移確率は $${\displaystyle \Pr(s_{t+1}\in S'\mid s_{t}=s,a_{t}=a)=\int _{s'\in S'}T(s,a,s')\,ds'}$$ によって記述される。

MDP における基本的な問題設定は、現在の状態が与えられたときに意思決定者の取る行動を既定する方策 (policy) を求めることである。 具体的には、方策とは MDP のある状態 ${\displaystyle s\in S}$ に対して定められる写像であり、次のように意思決定者の行動を規定する。

• 決定論的方策 (deterministic policy) : ${\displaystyle a_{t}=\pi (s)}$
• 確率的方策 (stochastic policy) : ${\displaystyle \Pr(a_{t}=a\mid s_{t}=s)=\pi (s,a)}$

方策 ${\displaystyle \pi }$ は、ある目的関数 (objective function) を最大化するようなものが選ばれる。 目的関数には、現在時刻から始まり十分時間が経過した後の時点における報酬の累積値が用いられる。 いま、時刻 ${\displaystyle \tau }$ において獲得する報酬を ${\displaystyle r_{\tau }\in \mathbb {R} }$ と表記すると、累積報酬の実現値は ${\displaystyle r_{t+1}+\cdots +r_{t+H}}$ で求められる。ただし、${\displaystyle H}$ は評価区間である。 ここで ${\displaystyle r_{\tau }}$ は確率変数であり、その実現値は MDP によって規定される状態遷移確率や方策に基づいて確率的に変動する。 したがって、実際の目的関数としては累積報酬の期待値である $${\displaystyle \mathbb {E} _{\pi }{\bigg [}\sum _{\tau =1}^{H}r_{t+\tau }\mid s_{t}=s{\bigg ]}}$$ が用いられる。 ただし、${\displaystyle \mathbb {E} _{\pi }[\cdot \mid s_{t}=s]}$ は方策 ${\displaystyle \pi }$ のもとでの（条件付き）期待値を意味する。 このように有限の時間区間における累積報酬を評価する問題設定は有限時間区間 (finite horizon) と呼ばれる。

行動が連続的に継続されるなどの場合においては、時間区間 ${\displaystyle H}$ を適切に設定することが困難となる。 そのような場合、無限時間区間 (infinite horizon) での問題設定が用いられる。 通常、期待値の収束性などの理由から有限時間区間における目的関数の ${\displaystyle H\to \infty }$ における極限を考えることは不可能であり、典型的には次のように時刻が進むにつれて「割引される」報酬の累積値 $${\displaystyle \mathbb {E} _{\pi }{\bigg [}\sum _{\tau =0}^{\infty }\gamma ^{\tau }r_{t+\tau +1}\mid s_{t}=s{\bigg ]}}$$ が用いられる。 ここで ${\displaystyle \gamma \in [0,1]}$ は割引率 (discount rate) と呼ばれる値であり、現在の報酬と未来の報酬との間における重要度の差異を表している。

モデルのマルコフ性により、ある時刻における目的関数の値は方策 ${\displaystyle \pi }$ を固定した下で状態 ${\displaystyle s_{t}\in S}$ の関数とみなすことが出来る。 このような考えのもと、ある方策 ${\displaystyle \pi \colon S\times A\to [0,1]}$ に対して定義される $${\displaystyle V^{\pi }(s)=\mathbb {E} _{\pi }{\bigg [}\sum _{\tau =0}^{\infty }\gamma ^{\tau }r_{t+\tau +1}\mid s_{t}=s{\bigg ]}}$$ を 状態価値関数 (state-value function) と呼ぶ。 状態価値関数は、現在の状態 ${\displaystyle s}$ からはじまり方策 ${\displaystyle \pi }$ によって行動を決定することで得られる（割引された）累積報酬の値であると解釈できる。 この状態価値関数 ${\displaystyle V^{\pi }(s)}$ は、次の整合性条件を満たす。 $${\displaystyle V^{\pi }(s)=\sum _{a\in A}\pi (s,a)\sum _{s'\in S}T(s,a,s'){\Big (}R(s,a,s')+\gamma V^{\pi }(s'){\Big )}}$$

任意の ${\displaystyle \pi '}$ および ${\displaystyle s\in S}$ に対し ${\displaystyle V^{\pi ^{*}}(s)\geq V^{\pi '}(s)}$ を満たす方策 ${\displaystyle \pi ^{*}}$ を最適方策 (optimal policy) と呼ぶ。 また、最適方策のもとでの状態価値関数 ${\displaystyle V^{*}(s)=V^{\pi ^{*}}(s)}$ は特に最適状態価値関数 (optimal state-value function)と呼ばれる。 最適状態価値関数は、次のベルマン方程式を満たす^[3]。 $${\displaystyle V^{*}(s)=\max _{a\in A}\sum _{s'\in S}T(s,a,s'){\Big (}R(s,a,s')+\gamma V^{*}(s'){\Big )}}$$

MDP は線形計画法または動的計画法で解くことができる。ここでは後者によるアプローチを示す．

価値反復法 (value iteration)^[1]は後ろ向き帰納法 (backward induction) とも呼ばれ、ベルマン方程式を満たす価値関数を繰り返し計算により求める。 ロイド・シャープレー が1953年に発表した確率ゲーム（英語版）に関する論文^[4]には価値反復法の特殊な場合が含まれるが、このことが認知されたのは後になってからである^[5]．

ステップ ${\displaystyle i}$における価値関数の計算結果を ${\displaystyle V_{i}(s)}$ と表記すると、価値反復法における更新式はつぎのように記述される: $${\displaystyle V_{i+1}(s)\leftarrow \max _{a\in A_{s}}\sum _{s'\in S}T(s,a,s'){\Big (}R(s,a,s')+\gamma V_{i}(s'){\Big )}\quad \forall s\in S}$$

上式をすべての状態において値が収束するまで繰り返したときの値を ${\displaystyle V^{\infty }(s)}$ とし、最適方策 ${\displaystyle \pi ^{*}}$ を次式で求める。

$${\displaystyle \pi ^{*}(s)\leftarrow \arg \max _{a\in A_{s}}\sum _{s'\in S}T(s,a,s'){\Big (}R(s,a,s')+\gamma V^{\infty }(s'){\Big )}\quad \forall s\in S}$$

方策反復法 (policy iteration)^[2]では、方策固定の下で行われる価値関数の更新 (policy evaluation) と、価値関数固定のもとで行われる方策の更新 (policy improvement) を交互に行うことで最適方策を求める。

1. 次の線形方程式を解き、価値関数を更新する

   ${\displaystyle V^{\pi }(s)=\sum _{a\in A}\pi (s,a)\sum _{s'\in S}T(s,a,s'){\Big (}R(s,a,s')+\gamma V^{\pi }(s'){\Big )}}$

2. 方策を次式で更新する

   ${\displaystyle \pi (s)\leftarrow \arg \max _{a\in A_{s}}\sum _{s'\in S}T(s,a,s'){\Big (}R(s,a,s')+\gamma V^{\pi }(s'){\Big )}\quad \forall s\in S}$

これらの操作を ${\displaystyle \pi }$ がすべての状態に対し変化しなくなるまで繰り返すことで、最適方策を得る。 方策反復法は離散値を取る方策の値が変化しなくなるという明確な終了条件を持つため有限時間でアルゴリズムが終了するという利点を持つ。

MDP では方策 ${\displaystyle \pi (s)}$ を計算する際に現在の状態 ${\displaystyle s}$ が既知であることを仮定している。 実際には状態観測に不確実性が伴う場合などこの仮定が成り立たない場合が多く、このような場合の一般化として部分観測マルコフ決定過程 (Partially Observable Markov Decision Process; POMDP) が用いられる。

状態遷移確率 ${\displaystyle T(s,a,s')}$ や報酬関数 ${\displaystyle R(s,a,s')}$ が未知の場合，環境との相互作用を通じてこれらの情報を得ながら行動を決定する必要がしばしば生じる．このような問題は強化学習の枠組みで議論される^[6]．

強化学習における代表的な学習アルゴリズムはQ学習と呼ばれるものである。 Q学習では、行動価値関数 (action-value function) と呼ばれる関数 ${\displaystyle Q^{\pi }(s,a)}$ に着目する。ここで ${\displaystyle Q^{\pi }(s,a)}$ は次のように定義される: $${\displaystyle Q^{\pi }(s,a)=\mathbb {E} _{\pi }[\sum _{t=0}^{\infty }\gamma ^{t}r_{t+1}|s_{0}=s,a_{0}=a]}$$

いま，最適方策のもとでの行動価値関数 ${\displaystyle Q^{*}(s,a)=\max _{\pi }Q^{\pi }(s,a)}$ は ${\displaystyle V^{*}(s)=\max _{a}Q^{*}(s,a)}$ を満たす。 すなわち、${\displaystyle Q^{*}}$ を学習することができれば（モデルのパラメータを直接求めることなく）最適方策を獲得することができる。 Q学習では、各試行における遷移前後の状態と入力、および試行で得られる即時報酬の実現値をもとに ${\displaystyle Q(s,a)}$ の値を逐次更新する。 実際の学習プロセスでは、すべての状態を十分サンプリングするため確率的なゆらぎを含むよう学習時の行動が選択される。

強化学習では最適化に必要なパラメータの学習を状態遷移確率・報酬関数を介することなくおこなうことが出来る（価値反復法や方策反復法ではそれらの明示的な仕様（各状態間の遷移可能性，報酬関数の関数形など）を与える必要がある）。 状態数（および行動の選択肢）が膨大な場合、強化学習はしばしばニューラルネットワークなどの関数近似と組み合わせられる。

機械学習理論における MDP のもう一つの応用は学習オートマトン (Learning Automata) と呼ばれる。 これは環境が確率的な挙動を示す場合における強化学習の一つでもある。 学習オートマトンに関する最初の詳細な論文は 1974 年に Narendra と Thathachar によりまとめられた^[7]（そこでは有限状態オートマトンと明示的に記載されている）。 強化学習と同様，学習オートマトンのアルゴリズムも確率や報酬が未知の場合の問題を解くことができる。 Q学習の違いは，価値関数ではく学習の結果を探すために行動の確率を直接求めることである。 学習オートマトンは収束性が解析学の要領で厳密に証明されている^[8]．

制約付きマルコフ決定過程 (Constrained Markov Decision Process; CMDP) はマルコフ決定過程の拡張である。 MDP と CMDP には3つの基本的な違いがある^[9]:

• ある行動をほかのものの代わりに適用した後で（複数の）コストが発生する
• CMDP は線形計画法のみで解くことが出来る（動的計画法を用いることはできない）
• 終端時刻における方策が初期状態に依存する

CMDP の応用例は数多く存在し、最近ではロボット工学におけるモーションプランニングに用いられている^[10]。

• Reinforcement Learning An Introduction by Richard S. Sutton and Andrew G. Barto
• Learning to Solve Markovian Decision Processes by Satinder P. Singh
• Optimal Adaptive Policies for Markov Decision Processes by Burnetas and Katehakis (1997)
• ソフトウェアパッケージ
  • MDP Toolbox for MATLAB, GNU Octave, Scilab and R The Markov Decision Processes (MDP) Toolbox.
  • MDP Toolbox for Matlab - An excellent tutorial and Matlab toolbox for working with MDPs.
  • MDP Toolbox for Python A package for solving MDPs
  • SPUDD A structured MDP solver for download by Jesse Hoey

• 動的計画法
• ベルマン方程式
• 強化学習
• Q学習

表 話 編 歴 確率論
確率の歴史	アンドレイ・コルモゴロフ トーマス・ベイズ アンドレイ・マルコフ ジョゼフ・L・ドゥーブ 伊藤清
確率の定義	客観確率 統計的確率 古典的確率 公理的確率 主観確率 ベイズ確率 確率の拡張 外確率 負の確率
基礎概念	モデル 試行 結果 事象 標本空間 確率測度 確率空間 確率変数 確率変数の収束 確率分布 離散確率分布 連続確率分布 同時分布 周辺分布 条件付き確率分布 独立同分布 関数 確率質量関数 確率密度関数 累積分布関数 特性関数 用語 独立 期待値 モーメント 条件付き確率 条件付き期待値
確率の解釈	ベルトランの逆説 3囚人問題 モンティ・ホール問題 サンクトペテルブルクのパラドックス 合接の誤謬 ギャンブラーの誤謬
問題	壺問題 クーポンコレクター問題
法則・定理	ベイズの定理 大数の法則 中心極限定理 コルモゴロフの0-1法則 デ・フィネッティの定理 ウィーナー＝ヒンチンの定理
測度論	確率測度の拡張 カラテオドリの拡張定理 E.ホップの拡張定理 コルモゴロフの拡張定理 ヴィタリの収束定理 優収束定理 ラプラス原理 スコロホッドの表現定理
確率微分方程式	伊藤の補題
確率過程	独立増分過程 定常過程 マルチンゲール マルコフ過程 マルコフ性 マルコフ連鎖 マルコフ決定過程 部分観測マルコフ決定過程 マルコフ再生過程 ウィーナー過程 ブラウン運動 幾何ブラウン運動 非整数ブラウン運動 ベルヌーイ過程 ガウス過程 自己相似過程 経験過程 中華料理店過程 オルンシュタイン＝ウーレンベック過程
情報量	最大エントロピー原理 交差エントロピー 結合エントロピー カルバック・ライブラー情報量 相互情報量
応用	数理ファイナンス ブラック–ショールズ方程式 確率的ボラティリティモデル 系統学 ベイズ法
カテゴリ

この項目は、コンピュータに関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（PJ:コンピュータ/P:コンピュータ）。

• 表示
• 編集