Inwolucja (matematyka) – Wikipedia, wolna encyklopedia

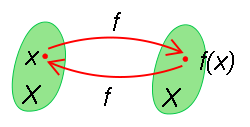
Inwolucja – funkcja, która ma funkcję odwrotną równą jej samej. Równoważnie jest to taka funkcja, która złożona sama ze sobą jest tożsamością^[1].

Z powyższych definicji wynika, że inwolucja musi być funkcją zbioru w ten sam zbiór: ${\displaystyle f\colon X\to X.}$ Definicja przez warunek ${\displaystyle f\circ f=\mathrm {id} _{X}}$ uogólnia się w teorii kategorii na morfizmy^{[potrzebny przypis]}.

Każda inwolucja, jako funkcja odwracalna, jest bijekcją (w przypadku morfizmów – izomorfizmem). Ponadto dla dowolnego ${\displaystyle k\in \mathbb {N} }$ jest

${\displaystyle f^{2k}=\mathrm {id} _{X}{\text{ oraz }}f^{2k+1}(x)=f.}$

Jeśli ${\displaystyle X^{Y}}$ oznacza zbiór wszystkich funkcji ${\displaystyle X\to Y,}$ zaś ${\displaystyle i\colon Y\to Y}$ jest inwolucją, to funkcja ${\displaystyle \mathrm {A} \colon X^{Y}\to X^{Y}}$ dana wzorem

${\displaystyle \mathrm {A} (f):=i\circ f}$

jest inwolucją. Podobnie jeżeli funkcja ${\displaystyle \mathrm {B} \colon Y^{Z}\to Y^{Z}}$ zdefiniowana jest wzorem

${\displaystyle \mathrm {B} (g):=g\circ i,}$

to jest ona inwolucją (własności te zachodzą dla morfizmów w dowolnej kategorii).

• Trywialnym przykładem inwolucji jest przekształcenie tożsamościowe. Inwolucją jest funkcja ${\displaystyle A^{2}\to A^{2},}$ czyli kwadratu kartezjańskiego zbioru ${\displaystyle A}$ w siebie dane wzorem ${\displaystyle (x,y)\mapsto (y,x);}$ zbiorem jej punktów stałych jest przekątna ${\displaystyle \Delta A:=\{(x,x)\colon x\in A\}.}$ Wiele inwolucji jest indukowanych przez tę inwolucję, np. transpozycja macierzy (opisana inwolucja jest z kolei indukowana przez transpozycję ciągu dwuelementowego, tzn. zamiany osi).
• Zmiana znaku ${\displaystyle x\mapsto -x}$ jest inwolucją w dowolnej grupie (w notacji addytywnej), a więc pierścieniu (np. liczb całkowitych) czy ciele (np. liczb wymiernych, rzeczywistych, zespolonych); odwrotność ${\displaystyle x\mapsto 1/x}$ jest inwolucją w grupie elementów odwracalnych (grupie multiplikatywnej ciała, np. liczb wymiernych, rzeczywistych czy zespolonych różnych od zera). Nietrywialną inwolucją liczb zespolonych jest sprzężenie. W rachunku macierzy inwolucjami są transpozycja, sprzężenie, sprzężenie hermitowskie (połączenie transpozycji i sprzężenia) oraz odwracanie macierzy.
• Z punktu widzenia algebry, a w szczególności teorii grup zasadniczo inwolucją nazywa się element rzędu dwa (czasami dopuszcza się też element rzędu pierwszego, czyli element neutralny; wynika to stąd, iż tworzą one podgrupę grupy symetrycznej złożonej ze wszystkich bijekcji ustalonego zbioru). W ten sposób permutacja jest inwolucją wtedy i tylko wtedy, gdy w jej rozkładzie na cykle występują tylko cykle długości 1 i 2; każda permutacja jest złożeniem dwóch inwolucji. Grupy Coxetera to grupy generowane przez inwolucje^[2].
• W geometrii euklidesowej inwolucjami są symetrie (m.in. symetria płaszczyznowa, osiowa, środkowa) oraz inwersja. Inwolucje są obiektem głębokich badań między innymi w topologii rozmaitości; patrz na przykład^[3].
• W teorii zbiorów inwolucjami są różnica symetryczna z ustalonym zbiorem czy dopełnienie zbioru (do przestrzeni), które jest inwolucją także w dowolnej algebrze Boole’a.
• W informatyce inwolucją jest szyfr Rot13.
• W teorii grafów inwolucją na zbiorze grafów planarnych jest graf dualny.
• W genetyce inwolucją jest nić komplementarna DNA.

Zobacz hasło inwolucja w Wikisłowniku

• działanie grupy na zbiorze

• Involution (ang.), Encyclopedia of Mathematics, encyclopediaofmath.org, [dostęp 2023-08-27].