Płaszczyzna zespolona – Wikipedia, wolna encyklopedia

Zasugerowano, aby zintegrować ten artykuł z artykułem diagram Arganda (dyskusja). Nie opisano powodu propozycji integracji.

Płaszczyzna zespolona, płaszczyzna Gaussa^[1] – geometryczny model ciała liczb zespolonych ${\displaystyle \mathbb {C} .}$ Płaszczyzna pełni w nim w stosunku do liczb zespolonych rolę analogiczną do roli, którą pełni prosta rzeczywista względem ciała liczb rzeczywistych.

Na płaszczyźnie wprowadzamy najpierw prostokątny kartezjański układ współrzędnych, na który składają się dwie prostopadłe do siebie osie współrzędnych przecinające się we wspólnym początku ${\displaystyle O.}$ Jedna z osi, oś ${\displaystyle OX,}$ jest pozioma (oś odciętych), skierowana od lewej strony do prawej, a druga pionowa ${\displaystyle OY}$ (oś rzędnych), jest skierowana od dołu do góry. Każdy punkt ${\displaystyle z}$ płaszczyzny jest jednoznacznie opisywany przez dwie współrzędne: odciętą ${\displaystyle x}$ i rzędną ${\displaystyle y,}$ będące odpowiednio współrzędnymi rzutów punktu ${\displaystyle z}$ na oś odciętych i oś rzędnych. Każdemu tak opisanemu punktowi płaszczyzny ${\displaystyle z=(x,y)}$ można przyporządkować liczbę zespoloną ${\displaystyle z=x+\mathbf {i} y}$^[2]:

${\displaystyle z=(x,y)\mapsto \mathbf {z} =x+\mathbf {i} y,}$ gdzie ${\displaystyle \mathbf {i} ={\sqrt {-1}}.}$

Przyporządkowanie to jest różnowartościowe i obrazem płaszczyzny jest w nim zbiór wszystkich liczb zespolonych. Zatem oba zbiory można utożsamić. W związku z tym oś odciętych nazywa się osią rzeczywistą, a oś rzędnych – osią urojoną (od pierwiastka kwadratowego z minus jedynki, nazywanego pierwiastkiem urojonym). Zapisujemy to następująco:

${\displaystyle \operatorname {Re} (\mathbf {z} )=x,\operatorname {Im} (\mathbf {z} )=y.}$

Działania na liczbach zespolonych określa się następująco. Niech

${\displaystyle \mathbf {z} _{1}=x_{1}+\mathbf {i} y_{1},\mathbf {z_{2}} =x_{2}+\mathbf {i} y_{2}.}$

Wtedy

${\displaystyle \mathbf {z} _{1}+\mathbf {z_{2}} =(x_{1}+x_{2})+\mathbf {i} (y_{1}+y_{2}),}$

${\displaystyle \mathbf {z} _{1}\cdot \mathbf {z_{2}} =(x_{1}\cdot x_{2}-y_{1}\cdot y_{2})+\mathbf {i} (x_{1}\cdot y_{2}+y_{1}\cdot x_{2}).}$

Stąd wynika, że działania dodawania i mnożenia na płaszczyźnie można określić następująco:

${\displaystyle (x_{1},y_{1})+(x_{2},y_{2})=(x_{1}+x_{2},y_{1}+y_{2}),}$

${\displaystyle (x_{1},y_{1})\cdot (x_{2},y_{2})=(x_{1}\cdot x_{2}-y_{1}\cdot y_{2},x_{1}\cdot y_{2}+y_{1}\cdot x_{2}).}$

Z definicji tych wynika, że:

• Dla punktów leżących na osi rzeczywistej oba działania można utożsamić z działaniami na liczbach rzeczywistych.
• Dla dowolnego punktu ${\displaystyle z=(x,y)}$ prawdziwa jest równość ${\displaystyle (1,0)\cdot (x,y)=(x,y).}$
• ${\displaystyle (0,1)\cdot (0,1)=(-1,0)}$ i bardziej ogólnie ${\displaystyle (0,1)\cdot (x,y)=(-y,x),}$ co oznacza, że mnożenie przez ${\displaystyle (0,1)}$ można zinterpretować na płaszczyźnie jako obrót dokoła środka współrzędnych o kąt 90°.

Wektorem na płaszczyźnie zespolonej nazywamy odpowiednio skierowany odcinek ${\displaystyle ab,}$ gdzie ${\displaystyle a,b\in \mathbb {C} .}$ Czasami mówi się nie o skierowanym odcinku, ale o parze uporządkowanej punktów. Punkt ${\displaystyle a}$ nazywamy początkiem wektora, a punkt ${\displaystyle b}$ nazywamy końcem wektora. Wektory ${\displaystyle ab}$ i ${\displaystyle cd}$ są równe, jeśli mają tę samą długość oraz są równoległe i jednakowo skierowane. Warunki te można zastąpić jednym:

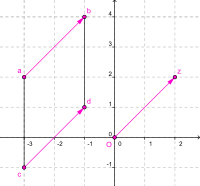
Czworokąt abcd jest równoległobokiem^[3].

Dla wektora ${\displaystyle ab}$ można określić jego długość ${\displaystyle |ab|}$ (długość odcinka ${\displaystyle ab}$) oraz współrzędne ${\displaystyle [x,y],}$ które są różnicami odpowiednich współrzędnych końca i początku wektora: Jeśli ${\displaystyle a=(x_{a},y_{a})}$ i ${\displaystyle b=(x_{b},y_{b}),}$ to

${\displaystyle ab=[x,y]=[x_{b}-x_{a},y_{b}-y_{a}],}$

${\displaystyle |ab|={\sqrt {x^{2}+y^{2}}}.}$

Wektory można mnożyć przez liczby rzeczywiste: Jeśli ${\displaystyle \alpha \in \mathbb {R} ,}$ to ${\displaystyle \alpha \cdot ab=\alpha \cdot [x,y]=[\alpha x,\alpha y].}$

Każdy wektor jest iloczynem pewnej liczby rzeczywistej nieujemnej (długości wektora) przez pewien wektor jednostkowy ${\displaystyle e{:}}$

${\displaystyle ab=|ab|\cdot {\bigg (}{\frac {1}{|ab|}}\cdot ab{\bigg )}=|ab|\cdot e.}$

Każda liczba zespolona ${\displaystyle z}$ wyznacza jednoznacznie wektor ${\displaystyle Oz}$ (wektor zaczepiony w punkcie ${\displaystyle O}$ o końcu w punkcie ${\displaystyle z}$). Każdy wektor jest równy dokładnie jednemu wektorowi o początku w punkcie ${\displaystyle O.}$ Tak więc zbiór liczb zespolonych można utożsamić ze zbiorem wektorów na płaszczyźnie: ${\displaystyle z\sim Oz.}$ Można zatem myśleć o liczbach zespolonych ${\displaystyle z}$ jako o wektorach ${\displaystyle z.}$ Długość wektora ${\displaystyle z}$ nazywamy modułem liczby zespolonej ${\displaystyle z}$ i oznaczamy ją ${\displaystyle |z|.}$

Dla dwóch wektorów ${\displaystyle z_{1}}$ i ${\displaystyle z_{2}}$ można określić ich sumę (${\displaystyle z_{1}}$ i ${\displaystyle z_{2}}$ są końcami wektorów o wspólnym początku ${\displaystyle O}$). W tym celu należy poprowadzić wektor ${\displaystyle z_{1}z_{3}}$ równy wektorowi ${\displaystyle z_{2}.}$ Wtedy ${\displaystyle z_{3}=z_{1}+z_{2}.}$ Suma tak określona jest przemienna, łączna i ma element neutralny – wektor zerowy.

Iloczyn wektorów (liczb zespolonych)^[4] ${\displaystyle z_{1}}$ i ${\displaystyle z_{2}}$ można określić dwustopniowo. Najpierw dla wektorów jednostkowych ${\displaystyle e_{1}}$ i ${\displaystyle e_{2},}$ gdzie ${\displaystyle z_{1}=|z_{1}|\cdot e_{1}}$ i ${\displaystyle z_{2}=|z_{2}|\cdot e_{2},}$ a następnie dla dowolnych liczb zespolonych, korzystając z równości:

${\displaystyle z_{1}\cdot z_{2}=(|z_{1}|\cdot |z_{2}|)\cdot (e_{1}\cdot e_{2}).}$

Dla wektorów jednostkowych ${\displaystyle e_{1}}$ i ${\displaystyle e_{2}}$ ich iloczynem jest wektor jednostkowy, którego kąt nachylenia do dodatniego kierunku osi ${\displaystyle Ox}$ jest sumą odpowiednich kątów nachylenia obu czynników.

Interpretacja ta łączy ze sobą geometrię analityczną, algebrę (w tym liniową ze względu na obecną strukturę liniową) oraz analizę. Możliwość utożsamienia liczb zespolonych z wektorami znana była już pod koniec XVIII wieku Wesselowi, mimo to przez długi czas jej autorstwo przypisywało się Argandowi, stąd też wspomnianą płaszczyzną nazywa się również płaszczyzną Arganda; inną spotykaną nazwą jest też płaszczyzna Gaussa ze względu na zasługi Gaussa na tym polu.

Z punktu widzenia geometrii analitycznej płaszczyzna zespolona to dwuwymiarowa przestrzeń liniowa nad ciałem liczb rzeczywistych z wprowadzonym działaniem mnożenia wektorów, co czyni z niej algebrę (przemienną), wyposażona w iloczyn skalarny, a przez to w indukowaną z niego normę (długość) daną jako moduł (pełniący analogiczną rolę do wartości bezwzględnej liczby rzeczywistej) i generowaną za jej pomocą metrykę (odległość).

Algebra zespolona jest pierścieniem z dzieleniem, co czyni z niej ciało-umożliwia to wprowadzenie na płaszczyźnie zespolonej geometrii inwersyjnej, choć wymaga to pamiętania przypadkach szczególnych (środku okręgu inwersyjnego, który nie jest w tym przekształceniu odwzorowywany). Dzięki bogatej strukturze liczby zespolone mogą służyć jako model geometrii euklidesowej (a więc i afinicznej), geometrii eliptycznej (a więc również rzutowej), czy geometria hiperboliczna. W niniejszym artykule omówiono geometrie euklidesową, afiniczną płaszczyzny zespolonej; pozostałe, wynikłe z obecności dzielenia w liczbach zespolonych opisano w artykule dotyczącym tzw. sfery Riemanna.

Na płaszczyźnie zespolonej wprowadza się układ współrzędnych biegunowych (bądź polarnych). Umożliwia to wyrażenie wektora ${\displaystyle \mathbf {z} }$ za pomocą jego długości ${\displaystyle \rho }$ (odległości od początku układu współrzędnych) oraz kąta skierowanego ${\displaystyle \varphi ,}$ którego pierwszym ramieniem jest ustalona półprosta – standardowo dodatnia półoś rzeczywista – a drugim dany wektor. W ten sposób wektorowi ${\displaystyle \mathbf {z} =[a,b]=[\rho ,\varphi ]}$ odpowiada liczba zespolona

${\displaystyle z=a+bi=\rho {\frac {a}{\rho }}+\rho {\frac {b}{\rho }}i=\rho (\cos \varphi +i\sin \varphi ),}$

gdyż części rzeczywista ${\displaystyle a}$ i urojona ${\displaystyle b}$ są rzutami prostokątnymi na odpowiednie osie, co oznacza, że ${\displaystyle \triangle \mathrm {oaz} }$ oraz ${\displaystyle \triangle \mathrm {obz} }$ są trójkątami prostokątnymi.

Dla danej liczby zespolonej ${\displaystyle z}$ liczbę rzeczywistą (wyznaczoną zgodnie z twierdzeniem Pitagorasa)

${\displaystyle \rho ={\sqrt {a^{2}+b^{2}}},}$

odpowiadającą długości ${\displaystyle |\mathbf {z} |}$ wektora ${\displaystyle \mathbf {z} }$ nazywa się modułem i oznacza ${\displaystyle |z|,}$ z kolei miarę kąta ${\displaystyle \varphi }$ nazywa się argumentem i oznacza ${\displaystyle \arg \;z.}$ Ponieważ zamiast miary ${\displaystyle \varphi }$ można użyć ${\displaystyle \varphi +k\cdot 360^{\circ }}$, gdzie ${\displaystyle k}$ to dowolna liczba całkowita, współrzędnych biegunowych liczby zespolonej nie można wyznaczyć w sposób jednoznaczny. Jeśli miara ${\displaystyle \varphi }$ spełnia nierówności ${\displaystyle 0\leqslant \varphi <360^{\circ }}$ bądź ${\displaystyle -180^{\circ }\leqslant \varphi <180^{\circ }}$ (w zależności od umowy, w dalszej części artykułu stosowana będzie pierwsza), to nazywa się ją argumentem głównym bądź wartością główną argumentu liczby ${\displaystyle z}$ i oznacza symbolem ${\displaystyle \operatorname {Arg} z.}$

Ponieważ dla dowolnej liczby rzeczywistej ${\displaystyle \varphi }$ zachodzi wzór Eulera,

${\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi ,}$

to liczbę zespoloną ${\displaystyle z}$ można przedstawić w układzie ${\displaystyle [\rho ,\varphi ]}$ również za pomocą wzoru

${\displaystyle z=\rho e^{i\varphi }.}$

O liczbie zespolonej ${\displaystyle z}$ wyrażonej jako ${\displaystyle a+bi}$ mówi się, że jest w postaci algebraicznej bądź kanonicznej, zaś przedstawionej jako ${\displaystyle \rho (\cos \varphi +i\sin \varphi )}$ nazywa liczbą zespoloną w postaci geometrycznej, trygonometrycznej bądź biegunowej; wyrażoną wzorem ${\displaystyle \rho \exp(i\varphi )}$ określa się jako liczbę zespoloną w postaci wykładniczej.

 Zobacz też: przestrzeń liniowa i przestrzeń afiniczna.

Niech liczbom zespolonym ${\displaystyle z=a+bi}$ oraz ${\displaystyle w=c+di}$ odpowiadają odpowiednio wektory

${\displaystyle \mathbf {z} =[a,b]=[\rho ,\varphi ]}$

oraz

${\displaystyle \mathbf {w} =[c,d]=[\sigma ,\theta ].}$

Wówczas działaniu dodawania liczb zespolonych ${\displaystyle z+w}$ odpowiada dodawanie wektorów

${\displaystyle \mathbf {z+w} =[a+c,b+d]=\left[{\sqrt {\tau }},\operatorname {sgn}(\sin \varphi +\sin \theta )\operatorname {arc\,cos} \;{\tfrac {\rho \cos \varphi +\sigma \cos \theta }{\sqrt {\tau }}}\right],}$

gdzie ${\displaystyle \tau =\rho ^{2}+2\rho \sigma \cos(\theta +\varphi )+\sigma ^{2},}$ przy czym liczbie ${\displaystyle 0}$ odpowiada wektor zerowy ${\displaystyle \mathbf {0} }$ (argument liczby ${\displaystyle 0}$ jest nieokreślony), zaś liczbie przeciwnej ${\displaystyle -z}$ do liczby ${\displaystyle z}$ odpowiada wektor przeciwny ${\displaystyle \mathbf {-z} }$ do wektora ${\displaystyle \mathbf {z} ,}$ tzn.

${\displaystyle \mathbf {-z} =-[a,b]=[-a,-b]}$

bądź

${\displaystyle \mathbf {-z} =-[\rho ,\varphi ]=[\rho ,\varphi \pm 180^{\circ }].}$

Odejmowanie liczb zespolonych:

${\displaystyle \mathbf {z-w} :=\mathbf {z+} (\mathbf {-w} ),}$

można wtedy określić wzorem

${\displaystyle \mathbf {z-w} =[a-c,b-d]=\left[{\sqrt {\tau }},\operatorname {sgn}(\sin \varphi -\sin \theta )\operatorname {arc\,cos} \;{\tfrac {\rho \cos \varphi -\sigma \cos \theta }{\sqrt {\tau }}}\right],}$

gdzie ${\displaystyle \tau =\rho ^{2}-2\rho \sigma \cos(\theta -\varphi )+\sigma ^{2}.}$ Działanie to pozwala wprowadzić na płaszczyźnie zespolonej strukturę afiniczną, bo dla każdych dwóch punktów ${\displaystyle z_{1}}$ i ${\displaystyle z_{2}{:}}$

${\displaystyle z_{2}=z_{1}+(z_{2}-z_{1}),}$

gdzie ${\displaystyle z_{2}-z_{1}}$ jest wektorem.

 Zobacz też: sprzężenie zespolone i przestrzeń euklidesowa.

Działanie mnożenia wektorów zdefiniowane jest jako

${\displaystyle \mathbf {zw} =[ac-bd,bc+ad]=[\rho \sigma ,\varphi +\theta ].}$

Dany wektor płaszczyzny zespolonej można poddać symetrii środkowej względem początku układu – wspomnianym odbiciem wektora ${\displaystyle \mathbf {z} }$ jest wektor ${\displaystyle \mathbf {-z} .}$ Wprowadza się także symetrię osiową płaszczyzny względem osi rzeczywistej – odbicie osiowe wektora ${\displaystyle \mathbf {z} }$ w poszczególnych układach dane jest jako

${\displaystyle {\overline {\mathbf {z} }}=[a,-b]=[\rho ,-\varphi ],}$

co w przypadku liczby zespolonej ${\displaystyle z}$ nazywa się sprzężeniem zespolonym liczby ${\displaystyle z.}$ Ponieważ sprzężenie (jako symetria) nie zmienia modułu liczby zespolonej (odległości), jest więc izometrią – oś rzeczywista jest prostą stałą tego przekształcenia. Za pomocą sprzężenia można zdefiniować również rzut na osie rzeczywistą i urojoną, odpowiednio

${\displaystyle \operatorname {re} z={\tfrac {1}{2}}(z+{\overline {z}})}$

oraz

${\displaystyle \operatorname {im} z={\tfrac {1}{2i}}(z-{\overline {z}}).}$

Na płaszczyźnie zespolonej można wprowadzić iloczyn skalarny,

${\displaystyle \mathbf {z} \cdot \mathbf {w} =ac+bd=\rho \sigma \cos(\varphi -\theta ),}$

który indukuje normę, którą jest moduł

${\displaystyle \rho =|\mathbf {z} |={\sqrt {\mathbf {z} \cdot \mathbf {z} }}={\sqrt {\mathbf {z{\overline {z}}} }}={\sqrt {a^{2}+b^{2}}},}$

wyznaczającą metrykę

${\displaystyle d(\mathbf {z} ,\mathbf {w} )=|\mathbf {z-w} |={\sqrt {(a-c)^{2}+(b-d)^{2}}}.}$

Ponadto ponieważ

${\displaystyle \mathbf {z{\overline {w}}} =[ac+bd,bc-ad]=[\rho \sigma ,\varphi -\theta ],}$

to ${\displaystyle \mathbf {z{\overline {w}}} }$ można traktować jako iloczyn geometryczny wektorów ${\displaystyle \mathbf {z} }$ i ${\displaystyle \mathbf {w} }$ będący sumą iloczynu wewnętrznego ${\displaystyle \cdot }$ (symetryczny iloczyn skalarny) i zewnętrznego ${\displaystyle \wedge }$ (antysymetryczny iloczyn wektorowy ${\displaystyle \times }$):

${\displaystyle \mathbf {z{\overline {w}}} =\mathbf {z} \cdot \mathbf {w} +\mathbf {z} \wedge \mathbf {w} =\mathbf {z} \cdot \mathbf {w} -i(\mathbf {z} \times \mathbf {w} ),}$

gdzie jednostka urojona ${\displaystyle i}$ pełni rolę pseudoskalara jednostkowego^[5] ustalającego dualność Hodge'a między iloczynem zewnętrznym i iloczynem wektorowym.

 Zobacz też: geometria syntetyczna.

Działanie dodawania, na płaszczyźnie przeprowadzane zwykle metodą równoległoboku – poszczególne elementy odpowiedniego równoległoboku oblicza się zgodnie z twierdzeniem cosinusów (działanie więc na rozwiązywaniu pewnego trójkąta), pozwala na przedstawienie przesunięć i wprowadza pojęcie równoległości.

Mnożenie przez skalar (liczbę rzeczywistą) wektora, które umożliwia mówienie o jednokładności – w przypadku płaszczyzny zespolonej nie jest to szczególnie interesujące ze względu na możliwość mnożenia wektora przez wektor (mnożenia dwóch liczb zespolonych), które daje dużo większe możliwości – umożliwia ono dodatkowo wprowadzenie obrotu. Tak więc mnożenie funkcjonalnie jest złożeniem obrotu i jednokładności o wspólnym środku – dowód geometryczny opiera się na podobieństwie trójkątów o wspólnym wierzchołku (dla iloczynu ${\displaystyle w}$ i ${\displaystyle v}$ należy rozpatrzeć trójkąty o wierzchołkach ${\displaystyle \mathrm {0,1,w} }$ oraz ${\displaystyle \mathrm {0,w,wv} }$): współczynnikiem podobieństwa jest skala jednokładności, zaś miara kąta obrotu to różnica miar kątów między wektorami. W szczególności mnożeniu przez ${\displaystyle i}$ odpowiada obrót o kąt ${\displaystyle 90^{\circ }.}$

W ten sposób uzyskuje się pełną grupę euklidesową przekształceń płaszczyzny zespolonej, gdyż zawiera ona każdą istotną izometrię płaszczyzny: tożsamość, przesunięcie (dodawanie), odbicie (sprzężenie), obrót (iloczyn skalarny, mnożenie). Biorąc pod uwagę strukturę liniową oznacza to, że figury płaszczyzny zespolonej można klasyfikować ze względu na podobieństwo (mnożenie).

Przekształcenie afiniczne parzyste płaszczyzny ${\displaystyle z\mapsto az+b,}$ gdzie ${\displaystyle a\neq 0}$ jest złożeniem obrotu o kąt ${\displaystyle \arg a}$ i jednokładności względem początku o skali ${\displaystyle |a|}$ oraz przesunięcia o ${\displaystyle b.}$ Do istotnych jego własności należą:

• przekształcanie okręgów na okręgi;
• odwzorowywanie dowolnej prostej na prostą do niej równoległą, czyli bycie dylatacją;
• zachowywanie kątów skierowanych, czyli konforemność;
• zachowanie stosunku podziału ${\displaystyle (z,w,u)={\tfrac {u-z}{u-w}}.}$

Przekształcenie afiniczne nieparzyste płaszczyzny ${\displaystyle z\mapsto a{\overline {z}}+b,}$ gdzie ${\displaystyle a\neq 0}$ jest złożeniem odbicia względem osi rzeczywistej, obrotu o kąt ${\displaystyle \arg a}$ i jednokładności względem początku o skali ${\displaystyle |a|}$ oraz przesunięcia o ${\displaystyle b.}$ Wśród ważnych jego własności wymienia się:

• przekształcanie okręgów na okręgi;
• odwracanie kątów skierowanych, czyli antykonforemność;
• zachowanie stosunku podziału ${\displaystyle (z,w,u)={\tfrac {u-z}{u-w}}.}$

Jeśli przekształcenie afiniczne nie ma punktów stałych, to jest ono przesunięciem. Jeżeli ${\displaystyle a\neq 0,1,}$ to przekształcenie to ma dokładnie jeden punkt stały ${\displaystyle u}$ i w przypadku parzystym można je zapisać w postaci ${\displaystyle z^{*}-u=a(z-u),}$ a w przypadku nieparzystym można je przedstawić jako ${\displaystyle z^{*}-u=a({\overline {z}}-u),}$ gdzie ${\displaystyle z^{*}}$ oznacza obraz tego przekształcenia w punkcie ${\displaystyle z,}$ zaś ${\displaystyle u={\tfrac {b}{1-a}}.}$ Wówczas przekształcenie afiniczne jest złożeniem obrotu wokół ${\displaystyle u}$ o kąt ${\displaystyle \arg a}$ (w przypadku parzystym) bądź odbicia względem prostej przechodzącej przez ${\displaystyle u}$ (w przypadku nieparzystym) oraz jednokładności o skali ${\displaystyle |a|}$ i środku ${\displaystyle u,}$ a więc przekształceniem liniowym. Przekształcenie afiniczne, które ma dwa punkty stałe jest tożsamością.

Ogólnym przekształceniem afinicznym nazywa się odwzorowanie ${\displaystyle z\mapsto az+b{\overline {z}}+c,}$ gdzie ${\displaystyle |a+b|\neq 0.}$ Zachowuje ono okręgi oraz miary kątów oraz stosunek podziału odcinka. Przekształcenia afiniczne parzyste tworzą podgrupę dylatacji-translacji grupy przekształceń afinicznych.

Niżej przedstawiono kilka przykładów zbiorów opisujących istotne figury na płaszczyźnie zespolonej:

• symetralna odcinka ${\displaystyle \mathrm {ab} ,}$ gdzie ${\displaystyle a\neq b,}$

  ${\displaystyle {\big \{}z\colon |z-a|=|z-b|{\big \}},}$

• okrąg o środku ${\displaystyle B/A}$ i promieniu ${\displaystyle {\sqrt {|B|^{2}-AC}}/|A|,}$ gdzie ${\displaystyle A\neq 0,\;A,C\in \mathbb {R} ,\;|B|^{2}>AC,}$

  ${\displaystyle {\big \{}z\colon A|z|^{2}-{\overline {B}}z-B{\overline {z}}+C=0{\big \}},}$

• okrąg przechodzący przez trzy liniowo niezależne (tzn. parami niewspółliniowe) punkty ${\displaystyle z_{1},z_{2},z_{3},}$

  ${\displaystyle \left\{z\colon \det {\begin{bmatrix}|z|^{2}&z&{\overline {z}}&1\\|z_{1}|^{2}&z_{1}&{\overline {z_{1}}}&1\\|z_{2}|^{2}&z_{2}&{\overline {z_{2}}}&1\\|z_{3}|^{2}&z_{3}&{\overline {z_{3}}}&1\end{bmatrix}}=0\right\}.}$

 Osobny artykuł: płaszczyzna S.

Analiza zespolona zajmuje się przede wszystkim funkcjami zespolonymi, tzn. przekształceniami odwzorowującymi podzbiór płaszczyzny zespolonej w inny (być może mający część wspólną lub nawet ten sam) podzbiór. Z tego powodu o elementach dziedziny ${\displaystyle f(z)}$ mówi się często, że leżą w „płaszczyźnie ${\displaystyle z}$” bądź „${\displaystyle z}$-płaszczyźnie”, z kolei obraz ${\displaystyle f(z)}$ nazywa się zbiorem punktów leżących na „płaszczyźnie ${\displaystyle w}$” bądź „${\displaystyle w}$-płaszczyźnie”; symbolicznie

${\displaystyle x+iy=z\mapsto w=u+iv,}$

gdzie ${\displaystyle f(z)=w.}$ Umożliwia to wyobrażenie przekształcenia ${\displaystyle f}$ jako odwzorowania płaszczyzny ${\displaystyle z}$ (ze współrzędnymi ${\displaystyle (x,y)}$) w płaszczyznę ${\displaystyle w}$ (ze współrzędnymi ${\displaystyle (u,v)}$).

W fizyce i inżynierii ${\displaystyle z}$-płaszczyznę interpretuje się jako dziedzinę czasu modelowaną za pomocą funkcji o wartościach parametryzowanych zmienną czasową. Bada się także tzw. „płaszczyznę ${\displaystyle s}$” lub „${\displaystyle s}$-płaszczyznę”, która służy odwzorowaniu dziedzin częstotliwości. Z punktu widzenia matematyki przejście od płaszczyzny ${\displaystyle z}$ do płaszczyzny ${\displaystyle s}$ polega na użyciu transformacji Laplace’a; w ten sposób płaszczyzna ${\displaystyle s}$ może służyć jako wygodne narzędzie umożliwiające graficzne przedstawienie tych transformacji. Dokładniej, rzeczywistą funkcję czasu przenosi się na płaszczyznę ${\displaystyle s}$ poprzez całkowanie funkcji z wagą ${\displaystyle e^{-st}}$ na całej prostej,

${\displaystyle \int _{-\infty }^{\infty }f(t)e^{-st}\,\mathrm {d} t,}$

przy czym ${\displaystyle s}$ oznacza zwyczajowo liczbę zespoloną.

Aby zrozumieć sposób działania powyższego przekształcenia, należy przywołać myśl przewodnią analizy harmonicznej: funkcje harmoniczne fal sinusoidalnych i cosinusoidalnych są domnażane do sygnału, zaś całkowanie wskazuje sygnał na danej częstotliwości (tzn. energię sygnału w danym punkcie dziedziny częstotliwości). Przekształcenie ${\displaystyle s,}$ znane szerzej jako transformacja Laplace’a, zachowuje się podobnie, lecz w większej ogólności: ${\displaystyle e^{-st}}$ nie tylko wychwytuje częstotliwości, ale także rzeczywiste oddziaływania ${\displaystyle e^{-t}.}$ W ten sposób umożliwia ono obserwację nie tylko odpowiedzi częstotliwościowej, ale także efektów opadania (ang. decay); przykładowo za pomocą przekształceń ${\displaystyle s}$ można poprawnie wymodelować wygaszoną falę sinusoidalną. Z własności transformacji Laplace’a wynika, że mnożenie przez ${\displaystyle s}$ w płaszczyźnie ${\displaystyle s}$ odpowiada różniczkowaniu w odpowiadającej jej rzeczywistej dziedzinie czasu, zaś dzielenie przez ${\displaystyle s}$ odpowiada całkowaniu.

W teorii sterowania płaszczyzny tej używa się np. do badania stabilności układu metodą Nyquista, która polega na analizie charakterystyki amplitudowo-fazowej układu opisanego transmitancją operatorową.

 Osobny artykuł: sfera Riemanna.

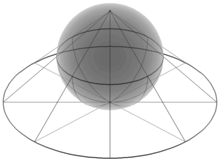
Dołączenie dodatkowego punktu ${\displaystyle \infty }$ do płaszczyzny zespolonej (tzn. uzwarcenie jej) umożliwia spójne przedstawienie homografii, a w szczególności odwzorowania inwersyjnego, które dzięki tej operacji określone jest na całej, tak rozszerzonej, płaszczyźnie zespolonej. Modelem tej płaszczyzny jest tzw. sfera Riemanna, czyli (dwuwymiarowa) sfera zanurzona w trójwymiarowej przestrzeni euklidesowej, dla której odpowiedniość między punktami sfery a punktami płaszczyzny zadana jest za pomocą rzutu stereograficznego określonego na całej sferze poza punktem rzutu. Choć przekształcenie to nie jest izometrią, tzn. nie zachowuje odległości, ani nie zachowuje pola, to jest konforemne, tzn. zachowuje kąty skierowane, wzajemnie jednoznaczne i gładkie.

Rozszerzenie płaszczyzny o punkt ${\displaystyle \infty }$ umożliwia odwzorowanie całej sfery (wraz z punktem rzutu), które zachowuje powyższe własności przekształcenia rzutowego. W ten sposób nabiera sensu np. odwzorowanie ${\displaystyle i(0)=\infty }$ w przekształceniu ${\displaystyle i(z)=z^{-1},}$ czyli inwersja środka okręgu. Jeśli wziąć pod uwagę naturalne przekształcenia sfery Riemanna, jakim jest konforemna homografia, czyli iloraz dwóch funkcji liniowych, to wszystkie proste na płaszczyźnie będą okręgami przechodzącymi przez punkt ${\displaystyle \infty .}$ Dzięki temu proste, nazywane „okręgami niewłaściwymi”, można traktować jako przypadek szczególny okręgów, co umożliwia zwięzłe sformułowania w rodzaju „w homografii okręgi przechodzą na okręgi” (tzn. tak prosta, jak i okrąg może być przeprowadzona na okrąg lub prostą).

• sfera Blocha

• JoannaJ. Jaszuńska JoannaJ., Liczby zespolone w geometrii, „Delta”, maj 2009, ISSN 0137-3005 [dostęp 2024-11-01] .
• Ilustracja przekształcenia s-płaszczyzny w z-płaszczyznę