Vetor potencial magnético – Wikipédia, a enciclopédia livre

Artigos sobre
Eletromagnetismo
Electricidade Magnetismo História [en] Livros didáticos [en]
Eletrostática Carga elétrica Lei de Coulomb Condutor Densidade de carga Permissividade Momento do dipolo elétrico Campo elétrico Potencial elétrico Fluxo elétrico / energia potencial Descarga electrostática Lei de Gauss Indução Isolante Densidade de polarização Eletricidade estática Efeito triboelétrico
Magnetostática Lei de Ampère Lei de Biot – Savart Lei de Gauss para o magnetismo Campo magnético Fluxo magnético Momento do dipolo magnético Permeabilidade magnética Potencial escalar magnético Magnetização [en] Força magnetomotriz Vetor potencial magnético Regra da mão direita [en]
Eletrodinâmica Lei da força de Lorentz Indução eletromagnética Lei de Faraday Lei de Lenz Corrente de deslocamento Equações de Maxwell Campo eletromagnético Pulso eletromagnético Radiação eletromagnética Tensor de Maxwell Vetor de Poynting Potentiais de Liénard – Wiechert Equações de Jefimenko Corrente de Foucault Equações de London [en] Descrições matemáticas do campo eletromagnético [en]
Circuito elétrico Corrente alternada Capacitância Corrente contínua Corrente elétrica Eletrólise Densidade de corrente elétrica Lei de Joule Força eletromotriz Impedância Indutância Lei de Ohm Circuito paralelo Resistência [en] Cavidades ressonantes [en] Circuito em série Tensão elétrica Guias de onda
Formulação covariante [en] Tensor eletromagnético (Tensor de tensão–energia) Quadricorrente Quadripotencial eletromagnético
Cientistas Ampère Biot Coulomb Davy Einstein Faraday Fizeau Gauss Heaviside Henry Hertz Hopkinson Jefimenko [en] Joule Lenz Liénard Lorentz Maxwell Neumann Ørsted Ohm Poynting Ritchie [en] Savart Singer [en] Steinmetz Tesla Thomson Volta Weber Wiechert Poisson
v d e

Vetor potencial magnético ou potencial do vetor magnético^[1][2], A, é a grandeza vetorial no eletromagnetismo clássico definida de modo que seu rotacional seja igual ao campo magnético: ${\textstyle \nabla \times \mathbf {A} =\mathbf {B} \,}$.^[3]

Junto ao potencial elétrico φ, o potencial do vetor magnético pode ser usado para especificar também o campo elétrico E. Portanto, muitas equações do eletromagnetismo podem ser escritas em termos de campos E e B, ou de forma equivalente em termos dos potenciais φ e A.^[4] Em teorias mais avançadas, como a mecânica quântica, a maioria das equações usa potenciais em vez de campos. Historicamente, Lord Kelvin introduziu pela primeira vez o potencial vetorial em 1851, junto à fórmula que o relaciona com o campo magnético.^[5]

O potencial do vetor magnético A é um campo vetorial, definido junto ao potencial elétrico ϕ (um campo escalar) pelas equações:^[6]

${\displaystyle \mathbf {B} =\nabla \times \mathbf {A} \,,\quad \mathbf {E} =-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}\,,}$

onde B é o campo magnético e E é o campo elétrico. Em magnetostática, onde não há distribuição de carga variável no tempo, apenas a primeira equação é necessária. (No contexto da eletrodinâmica, os termos potencial vetorial e potencial escalar são usados ​​para o potencial vetorial magnético e potencial elétrico, respectivamente. Em matemática, o potencial vetorial e o potencial escalar podem ser generalizados para dimensões superiores.)

Se os campos elétricos e magnéticos são definidos como acima a partir dos potenciais, eles satisfazem automaticamente duas das equações de Maxwell: a lei de Gauss para o magnetismo e a lei de Faraday. Por exemplo, se A é contínuo e bem definido em todos os lugares, então é garantido que não resultará em monopólos magnéticos. (Na teoria matemática dos monopólos magnéticos, A pode ser indefinido ou com valores múltiplos em alguns lugares; veja monopolo magnético para detalhes).

Começando com as definições acima:

${\displaystyle {\begin{aligned}\nabla \cdot \mathbf {B} &=\nabla \cdot \left(\nabla \times \mathbf {A} \right)=0\\\nabla \times \mathbf {E} &=\nabla \times \left(-\nabla \phi -{\frac {\partial \mathbf {A} }{\partial t}}\right)=-{\frac {\partial }{\partial t}}\left(\nabla \times \mathbf {A} \right)=-{\frac {\partial \mathbf {B} }{\partial t}}.\end{aligned}}}$

Alternativamente, a existência de A e ϕ é garantido a partir dessas duas leis usando o teorema de Helmholtz. Por exemplo, uma vez que o campo magnético é livre de divergência (lei de Gauss para o magnetismo; ou seja, ∇ ⋅ B = 0), sempre existe um A que satisfaz a definição acima.

O potencial do vetor Aé usado ao estudar o Lagrangiano na mecânica clássica e na mecânica quântica (veja a equação de Schrödinger para partículas carregadas, equação de Dirac e efeito Aharonov-Bohm).

No sistema SI, as unidades de A são V·s·m⁻¹ e são iguais ao momento por unidade de carga, ou força por unidade de corrente. No acoplamento mínimo, qA é chamado de momento potencial e faz parte do momento canônico.

A integral de linha de A sobre um "loop" fechado é igual ao fluxo magnético através da superfície fechada:

${\displaystyle \oint _{\Gamma }\mathbf {A} \,\cdot \,d{\mathbf {\Gamma } }=\iint _{S}\nabla \times \mathbf {A} \,\cdot \,d\mathbf {S} =\Phi _{B}.}$

Portanto, as unidades de A também são equivalentes a Weber por metro . A equação acima é útil na quantização de fluxo de loops supercondutores .

Embora o campo magnético B seja um pseudovetor (também chamado de vetor axial ), o potencial vetorial A é um vetor polar .^[7] Isso significa que se a regra da mão direita para produto vetorial fosse substituída por uma regra da mão esquerda, mas sem alterar nenhuma outra equação ou definição, então B trocaria de sinal, mas A não mudaria. Este é um exemplo de um teorema geral: a curva de um vetor polar é um pseudovetor e vice-versa.

A definição acima não define o potencial do vetor magnético exclusivamente porque, por definição, podemos adicionar arbitrariamente componentes livre de onda para o potencial magnético sem alterar o campo magnético observado. Portanto, há um certo grau de liberdade disponível ao escolher A. Esta condição é conhecida como invariância de calibre .

Usar a definição de potenciais acima e aplicá-la às outras duas equações de Maxwell resulta em uma equação diferencial que pode ser simplificada usando o medidor de Lorenz onde A é escolhido para satisfazer:

${\displaystyle \nabla \cdot \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}}=0.}$ ^[6]

Usando o medidor de Lorenz, as equações de Maxwell podem ser escritas compactamente em termos do potencial vetorial magnético A e do potencial escalar elétrico ϕ :^[6]

${\displaystyle {\begin{aligned}\nabla ^{2}\phi -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\phi }{\partial t^{2}}}&=-{\frac {\rho }{\epsilon _{0}}}\\\nabla ^{2}\mathbf {A} -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {A} }{\partial t^{2}}}&=-\mu _{0}\mathbf {J} \end{aligned}}}$

Em outros medidores, as equações são diferentes. Uma notação diferente para escrever essas mesmas equações (usando quatro vetores ) é mostrada abaixo.

As soluções das equações de Maxwell no medidor de Lorenz (ver Feynman ^[6] e Jackson ^[8] ) com a condição de contorno de que ambos os potenciais vão a zero suficientemente rápido à medida que se aproximam do infinito são chamadas de potenciais retardadores, que são o potencial do vetor magnético A(r, t) e o potencial escalar elétrico ϕ(r, t) devido a uma distribuição de corrente de densidade de corrente J(r′, t′), densidade de carga ρ(r′, t′), e volume Ω, dentro do qual ρ e J são diferentes de zero (pelo menos às vezes e em alguns lugares):

${\displaystyle {\begin{aligned}\mathbf {A} \left(\mathbf {r} ,t\right)&={\frac {\mu _{0}}{4\pi }}\int _{\Omega }{\frac {\mathbf {J} \left(\mathbf {r} ',t'\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} ^{3}\mathbf {r} '\\\phi \left(\mathbf {r} ,t\right)&={\frac {1}{4\pi \epsilon _{0}}}\int _{\Omega }{\frac {\rho \left(\mathbf {r} ',t'\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} ^{3}\mathbf {r} '\end{aligned}}}$

Onde os campos no vetor posição r e tempo t são calculados a partir de fontes na posição distante r' em um tempo anterior t'. A localização r ′ é um ponto fonte na distribuição de carga ou corrente (também a variável de integração, dentro do volume Ω ). O tempo anterior t ′ é chamado de tempo retardado e calculado como

${\displaystyle t'=t-{\frac {\left|\mathbf {r} -\mathbf {r} '\right|}{c}}}$ .

Existem algumas coisas notáveis sobre A e ϕ calculados desta forma:

• (A condição do medidor Lorenz ): ${\displaystyle \nabla \cdot \mathbf {A} +{\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}}=0}$ é satisfeito.
• A posição de r, o ponto em que os valores de ϕ e A são encontrados, só entra na equação como parte da distância escalar de r ′ a r . A direção de r ′ para r não entra na equação. A única coisa que importa sobre um ponto de origem é a distância dele.
• O integrando usa o tempo retardado, t ′. Isso simplesmente reflete o fato de que as mudanças nas fontes se propagam na velocidade da luz. Conseqüentemente, as densidades de carga e corrente que afetam o potencial elétrico e magnético em r e t, da localização remota r', também devem estar em algum tempo anterior t ′.
• A equação para A é uma equação vetorial. Em coordenadas cartesianas, a equação se separa em três equações escalares:^[9]

  ${\displaystyle {\begin{aligned}A_{x}\left(\mathbf {r} ,t\right)&={\frac {\mu _{0}}{4\pi }}\int _{\Omega }{\frac {J_{x}\left(\mathbf {r} ',t'\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} ^{3}\mathbf {r} '\\A_{y}\left(\mathbf {r} ,t\right)&={\frac {\mu _{0}}{4\pi }}\int _{\Omega }{\frac {J_{y}\left(\mathbf {r} ',t'\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} ^{3}\mathbf {r} '\\A_{z}\left(\mathbf {r} ,t\right)&={\frac {\mu _{0}}{4\pi }}\int _{\Omega }{\frac {J_{z}\left(\mathbf {r} ',t'\right)}{\left|\mathbf {r} -\mathbf {r} '\right|}}\,\mathrm {d} ^{3}\mathbf {r} '\end{aligned}}}$

Dessa forma, é fácil ver que o componente de A em uma dada direção depende apenas dos componentes de J que estão na mesma direção. Se a corrente for conduzida por um fio longo e reto, A aponta na mesma direção do fio.

Em outros medidores, a fórmula para A e ϕ é diferente.(Consulte o medidor de Coulomb para uma outra possibilidade.

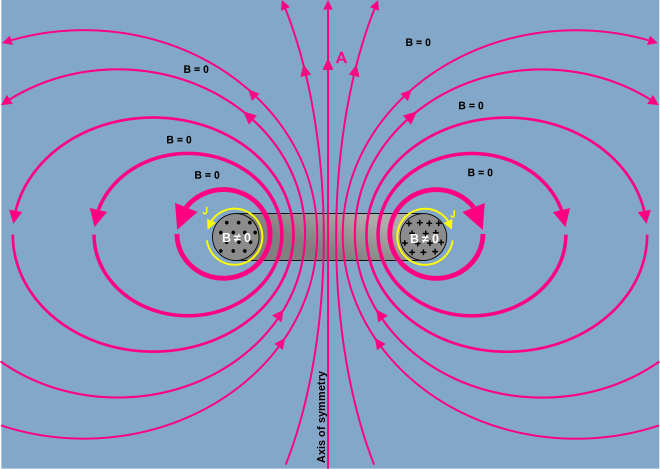
Veja Feynman ^[10] para a representação do campo A em torno de um solenoide longo e fino.

Desde a

${\displaystyle \nabla \times \mathbf {B} =\mu _{0}\mathbf {J} }$

assumindo condições quase estáticas, ou seja,

${\displaystyle {\frac {\partial E}{\partial t}}\rightarrow 0\,\quad \nabla \times \mathbf {A} =\mathbf {B} \,,}$

as linhas e contornos de A se relacionam com B como as linhas e contornos de B se relacionam com j . Assim, uma representação do campo A em torno de um loop de fluxo B (como seria produzido em um indutor toroidal ) é qualitativamente o mesmo que o campo B em torno de um loop de corrente.

A figura à direita é a representação artística do campo A. As linhas mais grossas indicam caminhos de intensidade média mais alta (caminhos mais curtos têm intensidade mais alta, de modo que a integral do caminho é a mesma). As linhas são desenhadas para (esteticamente) transmitir a aparência geral do A longe.

O desenho tacitamente assume ∇ ⋅ A = 0, verdadeiro sob uma das seguintes suposições:

• o medidor de Coulomb é assumido
• o medidor de Lorenz é assumido e não há distribuição de carga, ρ = 0 ,
• o medidor Lorenz é assumido e a frequência zero é assumida
• o medidor Lorenz é assumido e uma frequência diferente de zero que é baixa o suficiente para negligenciar ${\displaystyle {\frac {1}{c}}{\frac {\partial \phi }{\partial t}}}$ é assumido.

No contexto da relatividade especial, é natural juntar o potencial vetorial magnético com o potencial elétrico (escalar) no potencial eletromagnético, também chamado de quatro potenciais .

Uma motivação para fazer isso é que o quatro potenciais é um quadrivetor matemáticos. Assim, usando regras de transformação de quatro vetores padrão, se os potenciais elétricos e magnéticos são conhecidos em um referencial inercial, eles podem ser simplesmente calculados em qualquer outro referencial inercial.

Outra motivação relacionada é que o conteúdo do eletromagnetismo clássico pode ser escrito de uma forma resumida e conveniente usando o potencial eletromagnético quatro, especialmente quando o medidor de Lorenz é usado. Em particular, na notação de índice abstratos, o conjunto de equações de Maxwell (no calibre de Lorenz) pode ser escrito (em unidades gaussianas ) como segue:

${\displaystyle {\begin{aligned}\partial ^{\mu }A_{\mu }&=0\\\Box A_{\mu }&={\frac {4\pi }{c}}J_{\mu }\end{aligned}}}$

onde □ é o Operador de d'Alembert e J é a quatro correntes . A primeira equação é a condição de medidor de Lorenz, enquanto a segunda contém as equações de Maxwell. Os quatro potenciais também desempenham um papel muito importante na eletrodinâmica quântica .

• Efeito Aharonov-Bohm

Referências

• Duffin, W.J. (1990). Electricity and Magnetism, Fourth Edition. McGraw-Hill. [S.l.: s.n.] 
• Feynman, Richard P; Leighton, Robert B; Sands, Matthew (1964). The Feynman Lectures on Physics Volume 2. Addison-Wesley. [S.l.: s.n.] ISBN 0-201-02117-X 
• Jackson, John David (1999), Classical Electrodynamics, ISBN 0-471-30932-X 3rd ed. , John Wiley & Sons 
• Kraus, John D. (1984), Electromagnetics, ISBN 0-07-035423-5 3rd ed. , McGraw-Hill 

• Portal da física
• Portal da ciência