Pavare triunghiulară de ordinul 8

Pavare triunghiulară de ordinul 8
Pe modelul discului Poincaré al planului hiperbolic
Descriere
Tip	pavare hiperbolică
Configurația vârfului	3.3.3.3.3.3.3.3 (sau 38)
Configurația feței	V8.8.8 (sau V83)
Simbol Wythoff	8 | 3 2 4 | 3 3
Simbol Schläfli	{3,8} (3,4,3)
Diagramă Coxeter	sau
Grup de simetrie	[8,3], (*832) [(4,3,3)], (*433) [(4,4,4)], (*444)
Grup de rotație	[8,3]+, (832) [(4,3,3)]+, (433) [(4,4,4)]+, (444)
Poliedru dual	pavare octogonală de ordinul 3

În geometrie pavarea triunghiulară de ordinul 8 este o pavare hiperbolică regulată a planului hiperbolic cu simbolul Schläfli {3,8}, având opt triunghiuri regulate în jurul fiecărui vârf.

La simetria înjumătățită [1⁺,8,3] = [(4,3,3)] triunghiurile pot fi colorate alternând două culori.

Simetria [(4,4,4)] are 15 subgrupuri indexate mici (7 unice) prin eliminarea operatorilor de oglindire și alternare. Oglindirile pot fi eliminate dacă ordinele ramurilor lor sunt toate pare și se reduc ordinele ramurilor la jumătate. Eliminarea a două oglinzi lasă un punct de rotație cu ordinul la jumătate unde oglinzile eliminate se întâlnesc. În aceste imagini domeniile fundamentale sunt colorate alternativ alb-negru, iar oglindirile se fac la frontierele dintre culori. Adăugarea a 3 oglinzi care divid în două fiecare domeniu fundamental creează o simetrie 832. Subgrupul indexat-8, [(1⁺,4,1⁺,4,1⁺,4)] (222222) este subgrupul comutator^⁠(d) al [(4,4,4)].

Un subgrup mai mare [(4,4,4^*)], indice 8, este construit la fel cum (2*2222) cu punctele de rotație eliminate, devine (*22222222).

Simetria poate fi dublată la simetrie 842 adăugând un plan de oglindire de divizare peste domeniile fundamentale. Simetria poate fi extinsă la 6, ca simetrie 832, cu 3 plane de oglindire de divizare pe domeniu.

Subgrupuri indexate mici ale [(4,4,4)] (*444)

Indice	1	2			4
Diagramă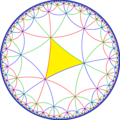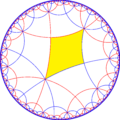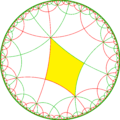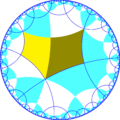
Coxeter	[(4,4,4)]	[(1+,4,4,4)] =	[(4,1+,4,4)] =	[(4,4,1+,4)] =	[(1+,4,1+,4,4)]	[(4+,4+,4)]
Orbifold	*444	*4242			2*222	222×
Diagramă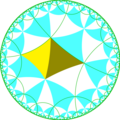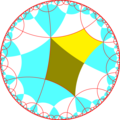
Coxeter		[(4,4+,4)]	[(4,4,4+)]	[(4+,4,4)]	[(4,1+,4,1+,4)]	[(1+,4,4,1+,4)] =
Orbifold		4*22			2*222
Subgrupuri directe
Indice	2	4			8
Diagramă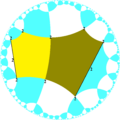
Coxeter	[(4,4,4)]+	[(4,4+,4)]+ =	[(4,4,4+)]+ =	[(4+,4,4)]+ =	[(4,1+,4,1+,4)]+ =
Orbifold	444	4242			222222
Subgrupuri rădăcină
Indice	8			16
Diagramă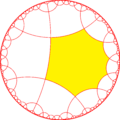
Coxeter	[(4,4*,4)]	[(4,4,4*)]	[(4*,4,4)]	[(4,4*,4)]+	[(4,4,4*)]+	[(4*,4,4)]+
Orbifold	*22222222			22222222

Variante de pavări regulate cu simetrie: *n32
Sferice				Euclid.	Hiperb. compacte		Paraco.	Hiperbolice necompacte
3.3	33	34	35	36	37	38	3∞	312i	39i	36i	33i

Dintr-o construcție Wythoff se obțin zece pavări uniforme ale planului hiperbolic, care pot fi bazate pe pavarea octogonală regulată și pavarea triunghiulară de ordinul 8.

Desenând dalele colorate în roșu pe fețele originale, galben la vârfurile originale și albastru de-a lungul laturilor, există 10 forme.

Pavări uniforme octogonale/triunghiulare
Simetrie: [8,3], (*832)							[8,3]+ (832)	[1+,8,3] (*443)		[8,3+] (3*4)
{8,3}	t{8,3}	r{8,3}	t{3,8}	{3,8}	rr{8,3} s2{3,8}	tr{8,3}	sr{8,3}	h{8,3}	h2{8,3}	s{3,8}
								sau	sau
Duale uniforme
V83	V3.16.16	V3.8.3.8	V6.6.8	V38	V3.4.8.4	V4.6.16	V34.8	V(3.4)3	V8.6.6	V35.4

Pavări regulate: {n,8}
Sferică	Pavări hiperbolice
{2,8}	{3,8}	{4,8}	{5,8}	{6,8}	{7,8}	{8,8}	...	{∞,8}

Poate fi generată și din pavările hiperbolice (4 3 3):

Pavări uniforme în planul hiperbolic (4 3 3)
Simetrie: [(4,3,3)], (*433)							[(4,3,3)]+, (433)
h{8,3} t0(4,3,3)	r{3,8}1/2 t0,1(4,3,3)	h{8,3} t1(4,3,3)	h2{8,3} t1,2(4,3,3)	{3,8}1/2 t2(4,3,3)	h2{8,3} t0,2(4,3,3)	t{3,8}1/2 t0,1,2(4,3,3)	s{3,8}1/2 s(4,3,3)
Duale uniforme
V(3.4)3	V3.8.3.8	V(3.4)3	V3.6.4.6	V(3.3)4	V3.6.4.6	V6.6.8	V3.3.3.3.3.4

Pavări uniforme în planul hiperbolic (4 4 4)
Simetrie: [(4,4,4)], (*444)							[(4,4,4)]+ (444)	[(1+,4,4,4)] (*4242)	[(4+,4,4)] (4*22)
t0(4,4,4) h{8,4}	t0,1(4,4,4) h2{8,4}	t1(4,4,4) {4,8}1/2	t1,2(4,4,4) h2{8,4}	t2(4,4,4) h{8,4}	t0,2(4,4,4) r{4,8}1/2	t0,1,2(4,4,4) t{4,8}1/2	s(4,4,4) s{4,8}1/2	h(4,4,4) h{4,8}1/2	hr(4,4,4) hr{4,8}1/2
Duale uniforme
V(4.4)4	V4.8.4.8	V(4.4)4	V4.8.4.8	V(4.4)4	V4.8.4.8	V8.8.8	V3.4.3.4.3.4	V88	V(4,4)3

• en John Horton Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• en „Chapter 10: Regular honeycombs in hyperbolic space”. The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678. 

• Materiale media legate de Pavare triunghiulară de ordinul 8 la Wikimedia Commons
• en Eric W. Weisstein, Hyperbolic tiling la MathWorld.
• en Eric W. Weisstein, Poincaré hyperbolic disk la MathWorld.
• en Hyperbolic and Spherical Tiling Gallery Arhivat în 24 martie 2013, la Wayback Machine.
• en KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• en Hyperbolic Planar Tessellations, Don Hatch

Portal Matematică