Retroprismă heptagramică

Retroprismă heptagramică
(model 3D)
Descriere
Tip	poliedru uniform, U80(b)
Fețe	16 (  2 heptagrame {7/4},       14 triunghiuri)
Laturi (muchii)	28
Vârfuri	14
χ	2
Configurația vârfului	3.3.3.7/4
Simbol Wythoff	| 2 2 7/4
Simbol Schläfli	sr{2,7/4}
Diagramă Coxeter
Grup de simetrie	D7h, [7,2], (*722), ordin 28
Grup de rotație	D7, [7,2]+, (722), ordin 14
Arie	${\displaystyle A=2A_{b}+A_{lat}}$
Volum	≈0,198 a3   (a = latura)
Poliedru dual	trapezoedru heptagramic concav
Proprietăți	stelată
Figura vârfului

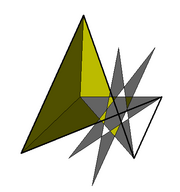În geometrie retroprisma heptagramică, sau antiprisma heptagramică 7/4 este o antiprismă cu baza heptagramică {7/4}. Are 16 fețe, 28 de laturi și 14 vârfuri.^[1] Având 16 fețe, este un hexadecaedru. Topologic este identică cu antiprisma heptagonală. Diferă de antiprisma heptagramică 7/3 prinfaptul că cele două heptagrame sunt orientate în opoziție.

Dacă fețele sunt toate regulate, retroprisma heptagramică este un poliedru semiregulat, mai general, un poliedru uniform cu indicele U_80(b).^[2] Este a doua într-un șir infinit de retroprisme formate din fețe laterale triunghiulare și două baze poligonale stelate regulate. Are simbolul Schläfli sr{2,7/4}.

Grupul de simetrie al unei retroprisme heptagramice drepte este D_7h^[1] de ordinul 28. Grupul de rotație este D₇ de ordinul 14.

Zonele bazelor corespunzătoare dintre fațetelor triunghiulare din jurul heptagoanelor centrale formează un interior ambiguu datorită autointersectării. Regiunile pe care le mărginesc ele pote fi considerate de interior sau exterior, în funcție de modul în care este definit interiorul. O definiție a interiorului este ca fiind mulțimea punctelor care au o rază care traversează frontiera domeniului de un număr impar de ori pentru a ieși din perimetru. Însă din regiunile respective razele care traversează o față laterală mai traversează încă o față, laterală sau nu.

Coordonatele carteziene ale vârfurilor unei antiprisme heptagramice cu lungimea laturilor de ${\displaystyle 2\sin {\frac {3\pi }{7}}}$sunt date de:^[1]

${\displaystyle \left(\,1,\,0,\,\pm H\,\right)}$

${\displaystyle \left(\,\cos {\frac {2\pi }{7}},\,\pm \sin {\frac {2\pi }{7}},\,\pm H\,\right)}$

${\displaystyle \left(\,\cos {\frac {4\pi }{7}},\,\pm \sin {\frac {4\pi }{7}},\,\pm H\,\right)}$

${\displaystyle \left(\,\cos {\frac {6\pi }{7}},\,\pm \sin {\frac {6\pi }{7}},\,\pm H\,\right)}$

unde

${\displaystyle H={\sqrt {\frac {1-2\cos {\frac {3\pi }{7}}}{2-2\cos {\frac {3\pi }{7}}}}}\sin {\frac {3\pi }{7}}.}$

Raza circumscrisă a retroprismei heptagramice cu lungimea laturilor a este:^[1]

${\displaystyle R={\frac {1}{4}}{\sqrt {\cot ^{2}{\frac {2\pi }{7}}+5}}\,a\approx 0,593505\,a.}$

Următoarea formulă pentru volum V este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:

${\displaystyle V={\frac {7}{12}}{\sqrt {4\cos ^{2}{\frac {2\pi }{14}}-1}}{\frac {\sin {\frac {6\pi }{7}}}{\sin ^{2}{\frac {4\pi }{7}}}}\,a^{3}\approx 0,198370\,a^{3}.}$

Poliedrul dual al antiprismei heptagramice 7/3 este trapezoedrul heptagramic 7/4.^[1]

• Lista poliedrelor uniforme

Portal Matematică

• Materiale media legate de retroprismă heptagramică la Wikimedia Commons