Triacontaedru disdiakis

Descriere
Triacontaedru disdiakis

(animație și model 3D))
Tip	Poliedru Catalan
Fețe	120 triunghiuri scalene, V4.6.10
Laturi (muchii)	180
Vârfuri	62
χ	2
Configurația vârfului	30×3⁴ + 20×3⁶ + 12×3¹⁰
Simbol Conway	mD sau dbD
Diagramă Coxeter
Grup de simetrie	I_h, H₃, [5,3], (*532)
Grup de rotație	I, [5,3]⁺, (532)
Unghi diedru	164° 53′ 17″ = = arccos(-179-24√5/241)
Poliedru dual	Icosidodecaedru trunchiat
Proprietăți	Poliedru convex, tranzitiv pe fețe
Desfășurată

În geometrie un triacontaedru disdiakis este un poliedru Catalan cu 120 de fețe. Fiecare poliedru Catalan este dualul unui poliedru arhimedic. Dualul triacontaedrului disdiakis este icosidodecaedrul trunchiat. Este tranzitiv pe fețe. Deși fețele sunt uniforme, ele sunt poligoane neregulate. Seamănă puțin cu un triacontaedru rombic umflat — dacă se înlocuiește fiecare față a triacontaedrului rombic cu un vârf și patru triunghiuri se ajunge cu un triacontaedru disdyakis. Adică, triacontaedrul disdiakis este Kleetop al triacontaedrului rombic. Are, de asemenea, cele mai multe fețe dintre toate poliedrele arhimedice fiind urmat ca număr de fețe de dodecaedrul snub, care are 92 de fețe.

Dacă bipiramidele, bipiramidele giroalungite și trapezoedrele sunt excluse, triacontaedrul disdiakis are cele mai multe fețe dintre orice alt poliedru strict convex unde fiecare față a poliedrului are aceeași formă.

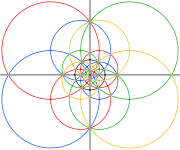
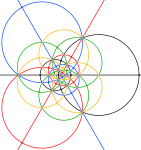
Proiectat într-o sferă, laturile unui triacontaedru disdiakis definesc 15 cercuri mari. Buckminster Fuller a folosit aceste 15 cercuri mari, împreună cu alte 10 și alte 6 din alte două poliedre pentru a-și defini cele 31 de cercuri mari ale icosaedrului sferic.

Fețe

Fețele unui triacontaedru disdiakis sunt triunghiuri scalene. Dacă $\varphi$ este secțiunea de aur atunci unghiurile lor vor fi $\arccos({\frac {-4\varphi +7}{30}})\approx 88,991\,801\,907\,82^{\circ }$ , $\arccos({\frac {-4\varphi +17}{20}})\approx 58,237\,919\,620\,89^{\circ }$ și $\arccos({\frac {5\varphi +2}{12}})\approx 32,770\,278\,471\,29^{\circ }$ .

Simetrie

Laturile poliedrului proiectate pe o sferă formează 15 cercuri mari și reprezintă toate cele 15 plane de oglindire ale simetriei icosaedrice I_h. Combinarea perechilor de triunghiuri reprezentate mai jos colorate într-o culoare deschisă și una întunecată (v. și desfășurata) definesc domeniile fundamentale ale simetriei icosaedrice nereflexive (I). Laturile unui compus de cinci octaedre definesc și ele cele 10 plane de oglindire ale simetriei icosaedrice.

Triacontaedru disdiakis	Hexacontaedru deltoidal	Triacontaedru rombic	Dodecaedru	Icosaedru	Piritoedru

Poliedru sferic

(animație)	Proiecții ortogonale după axele cu 2, 3 și 5 poziții

Proiecții stereografice

	cu 2 poziții	cu 3 poziții	cu 5 poziții


Colorat sub formă de compus de cinci octaedre, cu 3 cercuri mari pentru fiecare octaedru. Zonele din cercurile negre din rândul de jos corespund emisferei frontale a poliedrului sferic.

Proiecții ortogonale

Triacontaedrul disdiakis are trei tipuri de vârfuri, pe care pot fi centrate proiecțiile ortogonale:

Proiecții ortogonale
Simetrie proiectivă	[2]	[6]	[10]
Imagine
Imagine dual

Poliedre și pavări înrudite


Poliedrele asemănătoare cu triacontaedrul disdiakis sunt duale cu icosaedrul și dodecaedrul „papion”, conținând perechi suplimentare de fețe triunghiulare.^[1]

Familia de poliedre icosaedrice uniforme
Simetrie: [5,3], (*532)							[5,3]⁺, (532)


{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duale ale poliedrelor uniforme

V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Triacontaedrul disdiakis este înrudit topologic cu poliedrele definite de configurațiile fețelor V4.6.2n. Acest grup este particular pentru că toate poliedrele au un număr par de laturi la fiecare vârf și formează plane care divid poliedrele și liniile infinite din plan și continuă în planul hiperbolic pentru n ≥ 7. Cu un număr par de fețe la fiecare vârf, aceste poliedre și pavări pot fi colorate alternativ cu numai două culori, astfel încât toate fețele adiacente să aibă culori diferite.

Fiecare față de pe aceste domenii corespunde, de asemenea, domeniul fundamental al unui grup de simetrie cu ordinul 2,3,n plane de oglindire la fiecare vârf al feței triunghiulare. Acesta este *n32 în notația orbifold și [n,3] în notația Coxeter.

Variante de pavări omnitrunchiate cu simetrie n32: 4.6.2n*
Simetrie *n32 [n,3]	Sferice				Euclid.	Hiperb. compacte		Paraco.	Hiperbolice necompacte
Simetrie *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Imagini
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duale
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

Note

^ en Craig S. Kaplan, Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons Arhivat în 17 martie 2017, la Wayback Machine.

Bibliografie

en Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
en Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (The thirteen semiregular convex polyhedra and their duals, Page 25, Disdyakistriacontahedron)
en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss (2008), The Symmetries of Things, ISBN: 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 285, kisRhombic triacontahedron)

Legături externe

en Eric W. Weisstein, Disdyakis triacontahedron la MathWorld.
en Eric W. Weisstein, Catalan solid la MathWorld.
en Disdyakis triacontahedron (Hexakis Icosahedron) – Interactive Polyhedron Model

Portal Matematică

[1] Craig S. Kaplan, Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons Arhivat în 17 martie 2017, la Wayback Machine.

[1]