Трёхскатный прямой бикупол — Википедия

Трёхскатный прямой бикупол
(3D-модель)
Тип	многогранник Джонсона
Свойства	выпуклый
Комбинаторика
Элементы	14 граней 24 ребра 12 вершин Χ = 2
Грани	8 треугольников 6 квадратов
Конфигурация вершины	6(32.42) 6(3.4.3.4)
Двойственный многогранник	трапецеромбический додекаэдр
Развёртка
Классификация
Обозначения	J27, 2М4
Группа симметрии	D3h

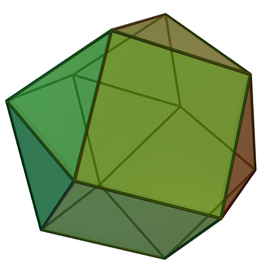
Трёхска́тный прямо́й бику́пол^[1] — один из многогранников Джонсона (J₂₇, по Залгаллеру — 2М₄).

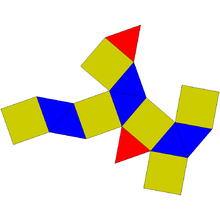
Составлен из 14 граней: 8 правильных треугольников и 6 квадратов. Каждая квадратная грань окружена квадратной и тремя треугольными; среди треугольных граней 2 окружены тремя квадратными, остальные 6 — двумя квадратными и треугольной.

Имеет 24 ребра одинаковой длины. 3 ребра располагаются между двумя квадратными гранями, 18 рёбер — между квадратной и треугольной, остальные 3 — между двумя треугольными.

У трёхскатного прямого бикупола 12 вершин. В каждой сходятся две квадратных и две треугольных грани.

Трёхскатный прямой бикупол можно получить из кубооктаэдра, разделив его на две половины, каждая из которых представляет собой трёхскатный купол (J₃), и повернув одну из них на 60° вокруг её оси симметрии.

• 
  Кубооктаэдр
• 
  Трёхскатный прямой бикупол

Объём и площадь поверхности при этом не изменятся; описанная и полувписанная сферы полученного многогранника также совпадают с описанной и полувписанной сферами исходного кубооктаэдра.

Если трёхскатный прямой бикупол имеет ребро длины ${\displaystyle a}$, его площадь поверхности и объём выражаются как

${\displaystyle S=\left(6+2{\sqrt {3}}\right)a^{2}\approx 9{,}4641016a^{2},}$

${\displaystyle V={\frac {5{\sqrt {2}}}{3}}\;a^{3}\approx 2{,}3570226a^{3}.}$

Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен

${\displaystyle R=a=1{,}0000000a;}$

радиус полувписанной сферы (касающейся всех рёбер в их серединах) —

${\displaystyle \rho ={\frac {\sqrt {3}}{2}}\;a\approx 0{,}8660254a.}$

С помощью трёхскатных прямых бикуполов можно замостить трёхмерное пространство без промежутков и наложений вместе с квадратными пирамидами (J₁) (см. иллюстрацию) или с правильными октаэдрами.

• Weisstein, Eric W. Трёхскатный прямой бикупол (англ.) на сайте Wolfram MathWorld.