Конструктивна блокова геометрія — Вікіпедія
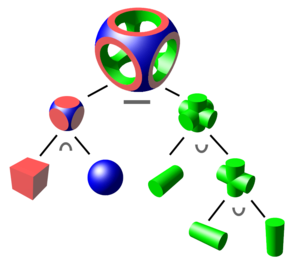
Конструктивна блокова геометрія (англ. Constructive Solid Geometry, скорочено CSG) — це технологія, яка використовується для моделювання твердих тіл. Конструктивна блокова геометрія дозволяє створити більш складну поверхню чи об'єкт як комбінацію простих об'єктів за допомогою бітових операцій.[1] Це дозволяє спростити математичний опис складних об'єктів, хоча для цього не завжди використовуються лише примітивні об'єкти.[2][3]
Конструктивна блокова геометрія часто, але не завжди, є способом моделювання в тривимірній графіці та САПР. КБУ також часто використовують у процедурному моделюванні. Так за допомогою конструктивної блокової геометрії представляють моделі або поверхні, які лише виглядають складними, а насправді вони являють собою більш хитро скомбіновані або декомбіновані прості об'єкти. В деяких випадках конструктивна блокова геометрія використовує полігональні сітки (англ. polygonal mesh), і може бути процедурною та/або параметричною.
Найпростіші тіла, які використовуються в конструктивній блокової геометрії називаються примітивами (англ. primitives). Як правило, це об'єкти, які мають просту форму: куб, циліндр, призма, піраміда, сфера, конус.[1] Набір доступних примітивів залежить від програмного забезпечення. Так, деякі програми дозволяють створення нових об'єктів конструктивно блокової геометрії на основі вигнутих об'єктів, а інші ні.
Побудова складнішого об'єкта відбувається шляхом застосування до об'єктів булевих (бітових) операцій на множинах — об'єднання, перетин і різниця, а також геометричні перетворення цих множин.[1]
Зазвичай примітив можна описати алгоритмом, який приймає декілька параметрів, наприклад: сфера може бути описана координатами центра разом зі значенням радіуса. Примітиви можуть бути об'єднані в складені об'єкти за допомогою таких операцій:
- Об'єднання
Злиття двох об'єктів в один - Різниця
Віднімання одного об'єкта від іншого - Перетин
Спільна частина обох об'єктів
Поєднуючи ці елементарні операції, можна будувати складні об'єкти на основі простих.
Конструктивна блокова геометрія (КБУ) має ряд практичних застосувань. Вона застосовується там, де необхідне використання простих геометричних об'єктів, або математична точність.[4] Майже у всіх інженерних пакетах САПР використовується КБУ (де це може бути корисно для представлення інструментів відсікань та функцій, де деталі повинні підганятися одна до одної).
Ігрові рушії, наприклад Quake engine, Unreal engine, Hammer (нативний редактор рівнів рушія Source), Torque Game Engine[en] / Torque Game Engine Advanced[en] використовують цю систему. Конструктивна блокова геометрія широко використовується, оскільки розробник може використовувати множину відносно простих об'єктів, щоб створити дуже складне геометричне зображення.[3] При використанні процедурної, або параметричної конструктивної блокової геометрії, користувач може переглянути свою складну геометричну фігуру, змінюючи положення об'єктів, або змінюючи логічні операції для комбінацій цих об'єктів.
Однією з переваг конструктивної блокової геометрії є те, що вона може гарантувати, що створені об'єкти є «твердими», або «водонепроникними», якщо всі примітивні форми є «водонепроникними».[5] Це може бути важливо для деяких виробничих або інженерних обчислювальних застосувань. Для порівняння, при створенні геометричних фігур на основі представлення границь, потрібен додатковий топологічний ряд даних або потрібно робити перевірку на узгодженість задля гарантії, що цей опис границі фігури вказує на чинний твердий об'єкт.[1]
Зручною властивістю об'єктів конструктивної блокової геометрії є те, що довільні точки легко класифікувати як всередині, так і поза формою, створеною КБУ. Точка просто класифікується за всіма базовими примітивами та обчислюється отриманий булевий вираз.[6] Це бажана опція для деяких програм, таких як трасування променів.[6]
Оскільки моделі конструктивної блокової геометрії параметризовані за конструкцією, вони часто вигідніші за полігональні сітки, коли справа стосується додатків, метою яких є виготовлення незалежних моделей. Для таких програм може бути корисним перетворити вже наявні сітки в дерева КБГ. Проблема автоматичного перетворення полігональних сіток у дерева конструктивної блокової геометрії називається оберненою КБГ.
Отримане дерево КБГ повинно займати той самий обсяг у тривимірному просторі, що і вхідна полігональна сітка, маючи мінімальну кількість вузлів. Перевагу віддають простим рішенням, щоб гарантувати, що отриману модель можна легко редагувати. Розв'язання цієї проблеми є складним завданням через великий простір пошуку, який потрібно дослідити. Він поєднує в собі безперервні параметри, такі як розмірність, розмір примітивних фігур і дискретні параметри, такі як булеві оператори, що використовуються для побудови остаточного дерева КБГ.
Дедуктивні методи розв'язують цю проблему шляхом побудови набору напівпросторів, що описують внутрішню будову геометричної фігури. Ці напівпростори використовуються для опису примітивів, які можна об'єднати, щоб отримати фінальну складну модель.[7]
Інший підхід поєднує в собі виявлення примітивних фігур та обчислення дерева КБГ, що визначає фінальну модель. Цей підхід використовує здатність сучасних засобів синтезу програм[en] знаходити дерево КБГ з мінімальною складністю.[8]
Існують також підходи, які використовують генетичні алгоритми для ітеративної оптимізації початкової форми у напрямку до форми бажаної полігональної сітки.[9]
- AutoCAD
- Autodesk Inventor
- Autodesk Fusion 360
- BRL-CAD
- CATIA
- FreeCAD
- NX CAD
- SolveSpaceAutoCAD
- Autodesk Inventor
- Autodesk Fusion 360
- BRL-CAD
- NIX CAD
- SolveSpace
- Onshape[en]
- OpenSCAD[en]
- PTC Creo[en] (раніше відомий як Pro/Engineer)
- Realsoft 3D
- Rhino
- SelfCAD
- Solid Edge[en]
- SolidWorks
- Tinkercad
- Vectorworks[en]
- ↑ а б в г Foley, James D.; Van, Foley Dan; Dam, Andries Van; Feiner, Steven K.; Hughes, John F.; Angel, Edward; Hughes, J. (1996). Computer Graphics: Principles and Practice (англ.). Addison-Wesley Professional. ISBN 978-0-201-84840-3. Архів оригіналу за 15 квітня 2021. Процитовано 24 травня 2021.
- ↑ Ray casting for modeling solids. Computer Graphics and Image Processing (англ.). Т. 18, № 2. 1 лютого 1982. с. 109—144. doi:10.1016/0146-664X(82)90169-1. ISSN 0146-664X. Архів оригіналу за 24 травня 2021. Процитовано 24 травня 2021.
- ↑ а б Bloomenthal, Jules; Bajaj, Chandrajit; Blinn, Jim; Wyvill, Brian; Cani, Marie-Paule; Rockwood, Alyn; Wyvill, Geoff (15 серпня 1997). Introduction to Implicit Surfaces (англ.). Morgan Kaufmann. ISBN 978-1-55860-233-5. Архів оригіналу за 23 квітня 2017. Процитовано 24 травня 2021.
- ↑ Constructive solid geometry. Wikipedia (англ.). 10 травня 2021. Процитовано 24 травня 2021.
- ↑ Ansari, Marwan (19 квітня 2016). Game Development Tools (англ.). CRC Press. ISBN 978-1-4398-6772-3. Архів оригіналу за 1 січня 2017. Процитовано 24 травня 2021.
- ↑ а б Glassner, Andrew S. (11 лютого 1989). An Introduction to Ray Tracing (англ.). Morgan Kaufmann. ISBN 978-0-12-286160-4. Архів оригіналу за 1 січня 2017. Процитовано 23 травня 2021.
- ↑ Three-dimensional halfspace constructive solid geometry tree construction from implicit boundary representations. Computer-Aided Design (англ.). Т. 36, № 11. 15 вересня 2004. с. 1063—1073. doi:10.1016/j.cad.2004.01.006. ISSN 0010-4485. Архів оригіналу за 24 травня 2021. Процитовано 24 травня 2021.
- ↑ Du, Tao; Inala, Jeevana Priya; Pu, Yewen; Spielberg, Andrew; Schulz, Adriana; Rus, Daniela; Solar-Lezama, Armando; Matusik, Wojciech (4 грудня 2018). InverseCSG: automatic conversion of 3D models to CSG trees. ACM Transactions on Graphics. Т. 37, № 6. с. 213:1–213:16. doi:10.1145/3272127.3275006. ISSN 0730-0301. Процитовано 24 травня 2021.
- ↑ ayolle, Pierre-Alain; Pasko, Alexander A. (2016) (PDF). Архів оригіналу (PDF) за 14 квітня 2021. Процитовано 24 травня 2021.
- ↑ Engine, Godot. Godot Engine - Godot gets CSG support. Godot Engine (англ.). Архів оригіналу за 24 травня 2021. Процитовано 24 травня 2021.
- ↑ Aqsis Renderer / News: Major release. sourceforge.net. Архів оригіналу за 24 травня 2021. Процитовано 24 травня 2021.
- Martti Mantyla, «An Introduction to Solid modeling», 1988
- Christoph M. Hoffman, «Geometric and Solid modeling», 1989
- Philip M. Hubbard, «Constructive Solid Geometry for Triangulated Polyhedra», 1990
- Michael Muuss & Lee Butler, Глава «Combinatorial Solid Geometry, B-Reps, and n-Manifold Geometry» з книги «State of the Art in Computer Graphics», 1991
- Leadwerks Software 'What is Constructive Solid Geometry?' — пояснення термінів, рівнянь та застосувань.
- GNU Triangulated Surface library [Архівовано 11 лютого 2021 у Wayback Machine.] — бібліотека з відкритим кодом (LGPL), яка містить можливості CSG на сітках з трикутників.
- Computational Geometry Algorithms Library [Архівовано 22 лютого 2011 у Wayback Machine.] — бібліотека з відкритим кодом (LGPL), яка містить, крім іншого, можливості CSG.
- The CSG rendering library [Архівовано 30 березня 2022 у Wayback Machine.] — бібліотека з відкритим кодом, яка виробляє орієнтований на зображення CSG-рендеринг з використанням OpenGL.
- HyperFun Project [Архівовано 17 грудня 2014 у Wayback Machine.] — проста функціональна мова для геометричного моделювання, здатний виконувати CSG-операції на різних типах об'єктів.
- Overview of CSG in avoCADo — програма 3D CAD з відкритим сирцевим кодом.
- SimpleGeo — інтерактивне твердотіле моделювання для симуляції переміщення часток за методом Монте-Карло.
- FMEpedia CSGBuilder example [Архівовано 5 грудня 2014 у Wayback Machine.] — wikipedia CSG binary tree as replicated using FME (Feature Manipulation Engine).
- SolidKit Library — програмна бібліотека для програм з 3D/2D-графікою, розроблена на C++ з використанням OpenGL, містить можливості CSG на сітках з трикутників.


 French
French Deutsch
Deutsch




