Список моделей многогранників Веннінґера — Вікіпедія

Стаття є індексованим списком рівномірних ззірчених многогранників з книги Маґнуса Веннінґера Моделі многогранників.

Книга була написана як методичка для побудови фізичних моделей многогранників. Вона включає шаблони та корисні поради для виготовлення, а також короткий опис теорії, що лежить в основі цих форм. Вона містить 75 непризматичних рівномірних многогранників, а також 44 ззірчення опуклих, правильних та майже правильних многогранників.

Цей список був створений для вшанування однієї з найперших робіт Веннінґера про многогранники і зробити детальний опис 119 нумерованих моделей з його книги.

Згадані тут моделі можна називати «N-ми моделлями Веннінґера», або коротко WN.

Многогранники згруповані в 5 таблиць: звичайні (1-5), майже правильні (6-18), правильні зірчасті многогранники (20-22,41), ззірчення і їх сполуки (19-66) і рівномірні зірчасті многогранники (67-119). Чотири правильні зірчасті многогранники перераховані двічі, позаяк вони належать до кожної з груп: правильних многогранників і ззірчень.

Платонові тіла (правильні) W1 до W5

[ред. | ред. код]
Номер Назва Зображення Альтернативна назва Альтернативне зображення Символ Вітгофа[en] Зображення вершин

і символ Шлефлі

Група симетрії U# K# V E F Грані за типом
1 Чотиригранник Чотиригранник 2 3

{3,3}

Td U01 K06 4 6 4 4{3}
2 Октаедр Hexahedron 2 3

{3,4}

Oh U05 K10 6 12 8 8{3}
3 Hexahedron (Куб) Октаедр 2 4

{4,3}

Oh U06 K11 8 12 6 6{4}
4 Ікосаедр Додекаедр 2 3

{3,5}

Ih U22 K27 12 30 20 20{3}
5 Додекаедр Ікосаедр 2 5

{5,3}

Ih U23 K28 20 30 12 12{5}

Архімедові тіла (майже правильні) W6 в W18

[ред. | ред. код]
Номер Назва Зображення Альтернативна назва Альтернативне зображення Символ Вітгофа Зображення вершин

і символ Шлефлі

Група симетрії U# K# V E F Грані за типом
6 Зрізаний тетраедр Тритетраедер Triakis tetrahedron 3

3.6.6

Td U02 K07 12 18 8 4{3} + 4{6}
7 Зрізаний октаедр Тетрагексаедер або пірамідний куб T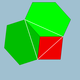etrakis hexahedron 3

4.6.6

Oh U08 K13 24 36 24 6{4} + 8{6}
8 Зрізаний куб Триоктаедер Triakis octahedron 4

3.8.8

Oh U09 K14 24 36 14 8{3} + 6{8}
9 Зрізаний ікосаедр 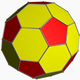Пентадодекаедер P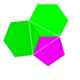entakis dodecahedron 3

5.6.6

Ih U25 K30 60 90 32 12{5} + 20{6}
10 Зрізаний додекаедр Триікосаедер Triakis icosahedron 5

3.10.10

Ih U26 K31 60 90 32 20{3} + 12{10}
11 Кубооктаедр ромбічний дванадцятигранник Rhombic dodecahedron 3 4

3.4.3.4

Oh U07 K12 12 24 14 8{3} + 6{4}
12 Ікосододекаедр Ромбічний тріаконтагедер Rhombic triacontahedron 3 5

3.5.3.5

Ih U24 K29 30 60 32 20{3} + 12{5}
13 Малий ромбо-кубічний октаедр Дельтоподібний ікосотетраедр Deltoidal icositetrahedron 2

3.4.4.4

Oh U10 K15 24 48 26 8{3}+(6+12){4}
14 Малий ромбічний ікосододекаедр deltoidal hexecontahedron Deltoidal hexecontahedron 2

3.4.5.4

Ih U27 K32 60 120 62 20{3} + 30{4} + 12{5}
15 Зрізаний кубічний октаедр

(Великий ромбічно-кубічний октаедр)

disdyakis dodecahedron Disdyakis dodecahedron

4.6.8

Oh U11 K16 48 72 26 12{4} + 8{6} + 6{8}
16 Зрізаний ікосододекаедр

(Great rhombicosidodecahedron)

disdyakis triacontahedron Disdyakis triacontahedron

4.6.10

Ih U28 K33 120 180 62 30{4} + 20{6} + 12{10}
17 Snub cube pentagonal icositetrahedron Pentagonal icositetrahedron 2 3 4

3.3.3.3.4

O U12 K17 24 60 38 (8 + 24){3} + 6{4}
18 Snub dodecahedron pentagonal hexecontahedron Pentagonal hexecontahedron 2 3 5

3.3.3.3.5

I U29 K34 60 150 92 (20 + 60){3} + 12{5}

Многогранники Кеплера–Пуансо (правильні зірчасті многогранники) W20, W21, W22, і W41

[ред. | ред. код]
Номер Назва Зображення Альтернативна назва Альтернативне зображення Символ Вітгофа Зображення вершин

і символ Шлефлі

Група симетрії U# K# V E F Грані за типом
20 Малий ззірчений додекаедр Великий додекаедр 25/2

{5/2,5}

Ih U34 K39 12 30 12 12{5/2}
21 Великий додекаедр Малий ззірчений додекаедр 2 5

{5,5/2}

Ih U35 K40 12 30 12 12{5}
22 Великий ззірчений додекаедр Великий ікосаедр 25/2

{5/2,3}

Ih U52 K57 20 30 12 12{5/2}
41 Великий ікосаедр

(16те ззірчення ікосаедра)

Великий ззірчений додекаедр 2 3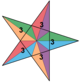

{3,5/2}

Ih U53 K58 12 30 20 20{3}

Ззірчення: моделі від W19 до W66

[ред. | ред. код]

Ззірчення октаедра

[ред. | ред. код]
Номер Назва Група симетрії Зображення Грані
2 Октаедр

(правильний)

Oh
19 Ззірчений восьмигранник

(Сполука двох тетраедрів)

Oh

Ззірчення додекаедра

[ред. | ред. код]
Індекс Назва Групи симетрії Зображення Грані
5 Додекаедр (правильний) Ih
20 Малий ззірчений додекаедр (правильний)

(Перше ззірчення додекаедра)

Ih
21 Великий додекаедр (правильний)

(Друге ззірчення додекаедра)

Ih
22 Великий ззірчений додекаедр (правильний)

(Третє ззірчення додекаедра)

Ih

Ззірчення ікосаедра

[ред. | ред. код]
Індекс Назва Групи симетрії Зображення Грані
4 Ікосаедр (правильний) Ih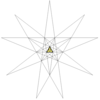
23 Сполука п'яти октаедрів

(Перше сполучне ззірчення ікосаедра)

Ih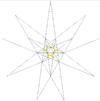
24 Сполука п'яти тетраедрів

(Друге сполучне ззірчення ікосаедра)

I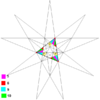
25 Сполука десяти тетраедрів

(Третє сполучне ззірчення ікосаедра)

Ih
26 Малий триамбічний ікосаедр

(Перше ззірчення ікосаедра)
(Триікосаедр)

Ih
27 Друге ззірчення ікосаедра Ih
28 Похідний додекаедр

(Третє ззірчення ікосаедра)

Ih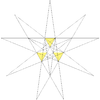
29 Четверте ззірчення ікосаедра Ih
30 П'яте ззірчення ікосаедра Ih
31 Шосте ззірчення ікосаедра Ih
32 Сьоме ззірчення ікосаедра Ih
33 Восьме ззірчення ікосаедра Ih
34 Дев'яте ззірчення ікосаедра

Великий триамбічний ікосаедр

 Ih
35 Десяте ззірчення ікосаедра I
36 Одинадцяте ззірчення ікосаедра I
37 Дванадцяте ззірчення ікосаедра Ih
38 Тринадцяте ззірчення ікосаедра I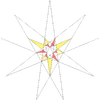
39 Чотирнадцяте ззірчення ікосаедра I
40 П'ятнадцяте ззірчення ікосаедра I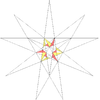
41 Великий ікосаедр (правильний)

(Шістнадцяте ззірчення ікосаедра)

Ih
42 Єхиднаедр
(останнє, сімнадцяте ззірчення форма ікосаедра) 		Ih

Ззірчення кубооктагедрона

[ред. | ред. код]
Індекс Назва Групи симетрії Зображення Грані (октаедричні площини) Грані (кубічні площини)
11 Кубооктаедр (правильний) Oh
43 Сполука куба і октаедра

(Перше ззірчення кубооктаедра)

Oh
44 Друге ззірчення кубооктаедра Oh
45 Третє ззірчення кубооктаедра Oh
46 Четверте ззірчення кубооктаедра Oh

Ззірчення ікосододекаедра

[ред. | ред. код]
Індекс Назва Групи симетрії Зображення Грані (ікосаедричні площини) Грані (додекаедричні площини)
12 Ікосододекаедр

(правильний)

Ih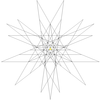
47 (Перше ззірчення ікосододекаедра)

Сполука додекаедра і ікосаедра

Ih
48 Друге ззірчення ікосододекаедра Ih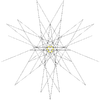
49 Третє ззірчення ікосододекаедра Ih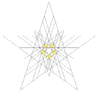
50 Четверте ззірчення ікосододекаедра

(Compound of small stellated dodecahedron
and triakis icosahedron)

Ih
51 П'яте ззірчення ікосододекаедра

(Compound of small stellated dodecahedron
an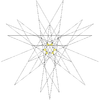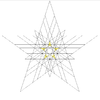d five octahedra)

Ih
52 Шосте ззірчення ікосододекаедра Ih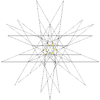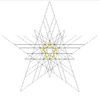
53 Сьоме ззірчення ікосододекаедра Ih
54 Восьме ззірчення ікосододекаедра

(Compound of five tetrahedra
a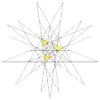nd great dodecahedron)

I
55 Дев'яте ззірчення ікосододекаедра Ih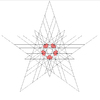
56 Десяте ззірчення ікосододекаедра Ih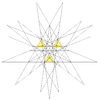
57 Одинадцяте ззірчення ікосододекаедра Ih
58 Дванадцяте ззірчення ікосододекаедра Ih
59 Тринадцяте ззірчення ікосододекаедра Ih
60 Чотирнадцяте ззірчення ікосододекаедра Ih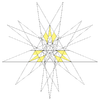
61 Сполука великого ззірченого додекаедра і великого ікосаедра Ih
62 П'ятнадцяте ззірчення ікосододекаедра Ih
63 Шістнадцяте ззірчення ікосододекаедра Ih
64 Сімнадцяте ззірчення ікосододекаедра Ih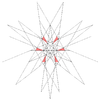
65 Вісімнадцяте ззірчення ікосододекаедра Ih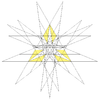
66 Дев'ятнадцяте ззірчення ікосододекаедра Ih

Рівномірні неопуклі тіла від W67 до W119

[ред. | ред. код]
Номер Назва Зображення Альтернативна назва Альтернативне зображення Символ Вітгофа Зображення вершин

і символ Шлефлі

Група симетрії U# K# V E F Грані за типом
67 Tetrahemihexahedron Tetrahemihexacron 2

4.3/2.4.3

Td U04 K09 6 12 7 4{3}+3{4}
68 Octahemioctahedron Octahemioctacron 3

6.3/2.6.3

Oh U03 K08 12 24 12 8{3}+4{6}
69 Small cubicuboctahedron Small hexacronic icositetrahedron 4

8.3/2.8.4

Oh U13 K18 24 48 20 8{3}+6{4}+6{8}
70 Small ditrigonal icosidodecahedron Small triambic icosahedron 5/23

(5/2.3)3

Ih U30 K35 20 60 32 20{3}+12{5/2}
71 Small icosicosidodecahedron Small icosacronic hexecontahedron 3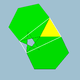

6.5/2.6.3

Ih U31 K36 60 120 52 20{3}+12{5/2}+20{6}
72 Small dodecicosidodecahedron Small dodecacronic hexecontahedron 5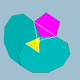

10.3/2.10.5

Ih U33 K38 60 120 44 20{3}+12{5}+12{10}
73 Dodecadodecahedron Medial rhombic triacontahedron 5/25

(5/2.5)2

Ih U36 K41 30 60 24 12{5}+12{5/2}
74 Small rhombidodecahedron Small rhombidodecacron

10.4.10/9.4/3

Ih U39 K44 60 120 42 30{4}+12{10}
75 Truncated great dodecahedron Small stellapentakis dodecahedron 5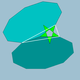

10.10.5/2

Ih U37 K42 60 90 24 12{5/2}+12{10}
76 Rhombidodecadodecahedron Medial deltoidal hexecontahedron 2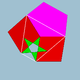

4.5/2.4.5

Ih U38 K43 60 120 54 30{4}+12{5}+12{5/2}
77 Great cubicuboctahedron Great hexacronic icositetrahedron 4/3

8/3.3.8/3.4

Oh U14 K19 24 48 20 8{3}+6{4}+6{8/3}
78 Cubohemioctahedron Hexahemioctacron 3

6.4/3.6.4

Oh U15 K20 12 24 10 6{4}+4{6}
79 Cubitruncated cuboctahedron

(Cuboctatruncated cuboctahedron)

Tetradyakis hexahedron

8/3.6.8

Oh U16 K21 48 72 20 8{6}+6{8}+6{8/3}
80 Ditrigonal dodecadodecahedron Medial triambic icosahedron 5/35

(5/3.5)3

Ih U41 K46 20 60 24 12{5}+12{5/2
81 Great ditrigonal dodecicosidodecahedron Great ditrigonal dodecacronic hexecontahedron 5/3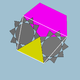

10/3.3.10/3.5

Ih U42 K47 60 120 44 20{3}+12{5}+12{10/3}
82 Small ditrigonal dodecicosidodecahedron 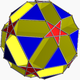Small ditrigonal dodecacronic hexecontahedron 5

10.5/3.10.3

Ih U43 K48 60 120 44 20{3}+12{5/2}+12{10}
83 Icosidodecadodecahedron Medial icosacronic hexecontahedron 3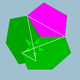

6.5/3.6.5

Ih U44 K49 60 120 44 12{5}+12{5/2}+20{6}
84 Icositruncated dodecadodecahedron

(Icosidodecatruncated icosidodecahedron)

Tridyakis icosahedron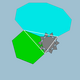

10/3.6.10

Ih U45 K50 120 180 44 20{6}+12{10}+12{10/3}
85 Nonconvex great rhombicuboctahedron

(Quasirhombicuboctahedron)

Great deltoidal icositetrahedron 2

4.3/2.4.4

Oh U17 K22 24 48 26 8{3}+(6+12){4}
86 Small rhombihexahedron Small rhombihexacron

4.8.4/3.8

Oh U18 K23 24 48 18 12{4}+6{8}
87 Great ditrigonal icosidodecahedron Great triambic icosahedron 3 5

(5.3.5.3.5.3)/2

Ih U47 K52 20 60 32 20{3}+12{5}
88 Great icosicosidodecahedron 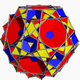Great icosacronic hexecontahedron 3

6.3/2.6.5

Ih U48 K53 60 120 52 20{3}+12{5}+20{6}
89 Small icosihemidodecahedron Small icosihemidodecacron 5

10.3/2.10.3

Ih U49 K54 30 60 26 20{3}+6{10}
90 Small dodecicosahedron Small dodecicosacron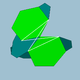

10.6.10/9.6/5

Ih U50 K55 60 120 32 20{6}+12{10}
91 Small dodecahemidodecahedron 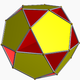Small dodecahemidodecacron 5

10.5/4.10.5

Ih U51 K56 30 60 18 12{5}+6{10}
92 Stellated truncated hexahedron

(Quasitruncated hexahedron)

Great triakis octahedron 4/3

8/3.8/3.3

Oh U19 K24 24 36 14 8{3}+6{8/3}
93 Great truncated cuboctahedron

(Quasitruncated cuboctahedron)

Great disdyakis dodecahedron

8/3.4.6

Oh U20 K25 48 72 26 12{4}+8{6}+6{8/3}
94 Great icosidodecahedron Great rhombic triacontahedron 5/23

(5/2.3)2

Ih U54 K59 30 60 32 20{3}+12{5/2}
95 Truncated great icosahedron Great stellapentakis dodecahedron 3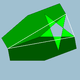

6.6.5/2

Ih U55 K60 60 90 32 12{5/2}+20{6}
96 Rhombicosahedron Rhombicosacron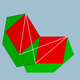

6.4.6/5.4/3

Ih U56 K61 60 120 50 30{4}+20{6}
97 Small stellated truncated dodecahedron

(Quasitruncated small stellated dodecahedron)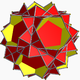

Great pentakis dodecahedron 5/3

10/3.10/3.5

Ih U58 K63 60 90 24 12{5}+12{10/3}
98 Truncated dodecadodecahedron

(Quasitruncated dodecahedron)

Medial disdyakis triacontahedron

10/3.4.10

Ih U59 K64 120 180 54 30{4}+12{10}+12{10/3}
99 Great dodecicosidodecahedron 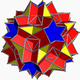Great dodecacronic hexecontahedron 5/3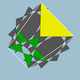

10/3.5/2.10/3.3

Ih U61 K66 60 120 44 20{3}+12{5/2}+12{10/3 }
100 Small dodecahemicosahedron Small dodecahemicosacron 3

6.5/3.6.5/2

Ih U62 K67 30 60 22 12{5/2}+10{6}
101 Great dodecicosahedron Great dodecicosacron

6.10/3.6/5.10/7

Ih U63 K68 60 120 32 20{6}+12{10/3}
102 Great dodecahemicosahedron Great dodecahemicosacron 3

6.5/4.6.5

Ih U65 K70 30 60 22 12{5}+10{6}
103 Great rhombihexahedron Great rhombihexacron

4.8/3.4/3.8/5

Oh U21 K26 24 48 18 12{4}+6{8/3}
104 Great stellated truncated dodecahedron

(Quasitruncated great stellated dodecahedron)

Great triakis icosahedron 5/3

10/3.10/3.3

Ih U66 K71 60 90 32 20{3}+12{10/3}
105 Nonconvex great rhombicosidodecahedron

(Quasirhombicosidodecahedron)

Great deltoidal hexecontahedron 2

4.5/3.4.3

Ih U67 K72 60 120 62 20{3}+30{4}+12{5/2}
106 Great icosihemidodecahedron Great icosihemidodecacron 5/3

10/3.3/2.10/3.3

Ih U71 K76 30 60 26 20{3}+6{10/3}
107 Great dodecahemidodecahedron Great dodecahemidodecacron 5/3

10/3.5/3.10/3.5/2

Ih U70 K75 30 60 18 12{5/2}+6{10/3}
108 Great truncated icosidodecahedron

(Great quasitruncated icosidodecahedron)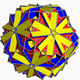

Great disdyakis triacontahedron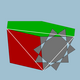

10/3.4.6

Ih U68 K73 120 180 62 30{4}+20{6}+12{10/3}
109 Great rhombidodecahedron Great rhombidodecacron

4.10/3.4/3.10/7

Ih U73 K78 60 120 42 30{4}+12{10/3}
110 Small snub icosicosidodecahedron Small hexagonal hexecontahedron 5/23 3

3.3.3.3.3.5/2

Ih U32 K37 60 180 112 (40+60){3}+12{5/2}
111 Snub dodecadodecahedron Medial pentagonal hexecontahedron 25/25

3.3.5/2.3.5

I U40 K45 60 150 84 60{3}+12{5}+12{5/2}
112 Snub icosidodecadodecahedron 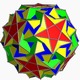Medial hexagonal hexecontahedron 5/33 5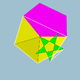

3.3.3.3.5.5/3

I U46 K51 60 180 104 (20+6){3}+12{5}+12{5/2}
113 Great inverted snub icosidodecahedron Great inverted pentagonal hexecontahedron 5/32 3

3.3.3.3.5/3

I U69 K74 60 150 92 (20+60){3}+12{5/2}
114 Inverted snub dodecadodecahedron 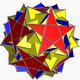Medial inverted pentagonal hexecontahedron 5/32 5

3.5/3.3.3.5

I U60 K65 60 150 84 60{3}+12{5}+12{5/2}
115 Great snub dodecicosidodecahedron Great hexagonal hexecontahedron 5/35/23

3.5/3.3.5/2.3.3

I U64 K69 60 180 104 (20+60){3}+(12+12){5/2}
116 Great snub icosidodecahedron Great pentagonal hexecontahedron 25/25/2

3.3.3.3.5/2

I U57 K62 60 150 92 (20+60){3}+12{5/2}
117 Великий вивернутий оберненокирпатий ікосододекаедр Great pentagrammic hexecontahedron 3/25/32

(3.3.3.3.5/2)/2

I U74 K79 60 150 92 (20+60){3}+12{5/2}
118 Small retrosnub icosicosidodecahedron Small hexagrammic hexecontahedron 3/23/25/2

(3.3.3.3.3.5/2)/2

Ih U72 K77 180 60 112 (40+60){3}+12{5/2}
119 Great dirhombicosidodecahedron Great dirhombicosidodecacron 3/25/335/2

(4.5/3.4.3.4.5/2.4.3/2)/2

Ih U75 K80 60 240 124 40{3}+60{4}+24{5/2}

Джерела

[ред. | ред. код]
  • Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
    • Уточнення
      • У Веннінґера, зображення вершин для W90 наведене не правильно, ніби у форми є паралельні ребра.
  • Wenninger, Magnus (1979). Spherical Models. Cambridge University Press. ISBN 0-521-29432-0.

Ланки

[ред. | ред. код]
Отримано з https://uk.wikipedia.org/wiki/Список_моделей_многогранників_Веннінґера