Архімедове тіло — Вікіпедія
В геометрії архімедове тіло (архімедів многогранник) — це високо симетричний напівправильний опуклий многогранник, гранями якого є два або більше типів правильних многокутників, що примикають до ідентичних вершин. Вони відрізняються від платонових тіл (правильних многогранників), які складаються тільки з одного типу многокутників в однакових вершинах, і від многогранників Джонсона, правильні многокутні грані яких належать різним типам вершин.
Тут поняття «ідентичні вершини» означає, що для будь-яких двох вершин існує ізометрія всього тіла, яка переводить одну вершину в іншу. Іноді тільки потрібно, щоб грані, прилеглі до однієї вершини, були ізометричними граням при іншій вершині. Ця різниця в термінах визначає, вважається подовжений квадратний гіробікупол[ru] (псевдоромбокубооктаедр) архімедовим тілом чи многогранником Джонсона — це єдиний опуклий многогранник, в якому многокутні межі примикають до вершини однаковим способом у кожній вершині, але многогранник не має глобальної симетрії, яка б переводила будь-яку вершину в будь-яку іншу. Ґрунтуючись на існуванні псевдоромбокубооктаедра, Ґрюнбаум[1] запропонував термінологічну відмінність, у якій архімедове тіло визначається як таке, що має одну і ту ж вершинну фігуру в кожній вершині (включно з подовженим квадратним гіробікуполом), тоді як однорідний многогранник визначається як тіло, у якого будь-яка вершина симетрична будь-який інший (що виключає гіробікупол[ru]).
Призми і антипризми, групами симетрій яких є діедричні групи, як правило, не вважаються архімедовим тілами, незважаючи на те, що вони підпадають під визначення, дане вище. З цим обмеженням існує тільки скінченне число архімедових тіл. Всі тіла, крім подовженого квадратного гіробікупола, можна отримати побудовами Вітгоффа з платонових тіл за допомогою тетраедричної, октаедричної[en] і ікосаедричної[ru] симетрій.
Архімедові тіла отримали назву на честь Архімеда, який обговорював їх у нині втраченій роботі. Папп посилається на цю роботу і стверджує, що Архімед перелічив 13 многогранників[1]. За часів Відродження художники і математики цінували чисті форми і перевідкрити їх усі. Ці дослідження були майже повністю закінчені близько 1620 року Йоганном Кеплером[2], який визначив поняття призм, антипризм і неопуклих тіл, відомих як тіла Кеплера - Пуансо.
Кеплер, можливо, знайшов також подовжений квадратний гіробікупол (псевдоромбоікосаедр) — щонайменше, він стверджував, що є 14 архімедових тіл. Однак його опубліковані переліки включають тільки 13 однорідних многогранників, і перше ясне твердження про існування псевдоромбоікосаедра зробив 1905 року Дункан Соммервіль[1].
Існує 13 архімедових тіл (не рахуючи подовженого квадратного гіробікупола; 15, якщо враховувати дзеркальні відображення двох енантіоморфів, які нижче перелічені окремо).
Тут вершинна конфігурація відноситься до типів правильних многокутників, які примикають до вершини. Наприклад, вершинна конфігурація (4,6,8) означає, що квадрат, шестикутник і восьмикутник зустрічаються у вершині (порядок переліку береться за годинниковою стрілкою відносно вершини).
| Назва (альтернативна назва) | Шлефлі Коксетер | Прозорий | Непрозорий | Розгортка | Вершинна фігура | Граней | Ребер | Вершин | Об'єм (за одинич- ного ребра) | Група точок | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Зрізаний тетраедр | {3,3} | (Обертання) |  | 3.6.6 | 8 | 4 трикутники 4 шестикутники | 18 | 12 | 2.710576 | Td | |
| Кубооктаедр (ромботетраедр) | r{4,3} або rr{3,3} | (Обертання) |  |  | 3.4.3.4 | 14 | 8 трикутників 6 квадратів | 24 | 12 | 2.357023 | Oh |
| Зрізаний куб | t{4,3} |  (Обертання) |  |  | 3.8.8 | 14 | 8 трикутників 6 восьмикутників | 36 | 24 | 13.599663 | Oh |
| Зрізаний октаедр (зрізаний тетратераедр) | t{3,4} або tr{3,3} |  |  |  | 4.6.6 | 14 | 6 квадратів 8 шестикутників | 36 | 24 | 11.313709 | Oh |
| Ромбокубооктаедр (малий ромбокубооктаедр) | rr{4,3} |  (Обертання) |  |  | 3.4.4.4 | 26 | 8 трикутників 18 квадратів | 48 | 24 | 8.714045 | Oh |
| Зрізаний кубооктаедр (великий ромбокубооктаедр) | tr{4,3} |  (Обертання) |  | 4.6.8 | 26 | 12 квадратів 8 шестикутників 6 восьмикутників | 72 | 48 | 41.798990 | Oh | |
| Кирпатий куб (кирпатий кубоктаедр) | sr{4,3} | (Обертання) |  | 3.3.3.3.4 | 38 | 32 трикутники 6 квадратів | 60 | 24 | 7.889295 | O | |
| Ікосододекаедр | r{5,3} |  (Обертання) |  | 3.5.3.5 | 32 | 20 трикутників 12 п'ятикутників | 60 | 30 | 13.835526 | Ih | |
| Зрізаний додекаедр | t{5,3} | (Обертання) |  |  | 3.10.10 | 32 | 20 трикутників 12 десятикутників | 90 | 60 | 85.039665 | Ih |
| Зрізаний ікосаедр | t{3,5} |  (Обертання) |  |  | 5.6.6 | 32 | 12 п'ятикутників 20 шестикутників | 90 | 60 | 55.287731 | Ih |
| Ромбоікосододекаедр (малий ромбоікосододекаедр) | rr{5,3} |  (Обертання) |  | 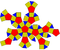 | 3.4.5.4 | 62 | 20 трикутників 30 квадратів 12 п'ятикутників | 120 | 60 | 41.615324 | Ih |
| Ромбозрізаний ікосододекаедр | tr{5,3} |  (Обертання) |  | 4.6.10 | 62 | 30 квадратів 20 шестикутників 12 десятикутників | 180 | 120 | 206.803399 | Ih | |
| Кирпатий додекаедр (кирпатий ікосододекаедр) | sr{5,3} |  (Обертання) |  | 3.3.3.3.5 | 92 | 80 трикутників 12 п'ятикутників | 150 | 60 | 37.616650 | I | |
Деякі визначення напівправильних многогранників включають ще одне тіло — подовжений квадратний гіробікупол або «псевдоромбокубооктаедр»[3].
Число вершин дорівнює відношенню 720° до кутового дефекту при вершині.
Кубоктаедр і ікосододекаедр є реберно-однорідними і називаються квазіправильними[ru].
Дуальні многогранники архімедових тіл називаються каталановими тілами. Разом з біпірамідами і трапецоедрами вони є гране-однорідними тілами з правильними вершинами.
Кирпатий куб і кирпатий додекаедр хіральні, оскільки вони з'являються в лівосторонньому і правосторонньому варіантах. Якщо щось має кілька видів, які є тривимірним дзеркальним відображенням один одного, ці форми називають енантіоморфами (ця назва застосовується також для деяких форм хімічних сполук).

Різні архімедові і платонові тіла можуть бути отримані одне з одного за допомогою декількох операцій. Починаючи з платонових тіл, можна використовувати операцію зрізання кутів. Для збереження симетрії зрізання виконується площиною, перпендикулярною до прямої, що з'єднує кут з центром многокутника. Залежно від того, наскільки глибоко виконується зрізання (див. таблицю нижче), отримаємо різні платонові і архімедові (й інші) тіла. Розширення[ru] або скошування[ru] здійснюється шляхом руху граней у напрямку від центра (на однакову відстань, щоб зберегти симетрію) і створенням, потім, опуклої оболонки. Розширення з поворотом здійснюється також обертанням граней, це ламає прямокутники, що виникають на місцях ребер, на трикутники. Остання побудова, яке ми тут розглянемо, це зрізання як кутів, так і ребер. Якщо нехтувати масштабування, розширення можна також розглядати як зрізання кутів і ребер, але з певним відношенням між зрізаннями кутів і ребер.
| Симетрія | Тетраедрична | Октаедрична[en]  | Ікосаедрична  | |||
|---|---|---|---|---|---|---|
| Початкове тіло Операція | Символ {p, q} | Тетраедр {3,3}  | Куб {4,3}  | Октаедр {3,4}  | Додекаедр {5,3} | Ікосаедр {3,5}  |
| Зрізання (t) | t{p, q} | Зрізаний тетраедр | Зрізаний куб | Зрізаний октаедр | Зрізаний додекаедр | Зрізаний ікосаедр |
| Повне зрізання (r) Амвон (a) | r{p, q} | Тетратетраедр | Кубооктаедр | Ікосододекаедр | ||
| Глибоке зрізання[en] (2t) (dk) | 2t{p, q} | Зрізаний тетраедр | Зрізаний октаедр | Зрізаний куб | Зрізаний ікосаедр | Зрізаний додекаедр |
| Подвійне повне зрізання (2r) Двоїстий (d) | 2r{p, q} | Тетраедр | Октаедр | Куб | Ікосаедр | Додекаедр |
| Скошування (rr) Розширення (e) | rr{p, q} | Кубооктаедр | Ромбокубооктаедр | Ромбоікосододекаедр  | ||
| Кирпате спрямлення (sr) Спрямлення[en] (s) | sr{p, q} | Кирпатий тетратетраедр | Кирпатий куб | Кирпатий ікосододекаедр | ||
| скіс-зрізання[en] (tr) Скошування (b) | tr{p, q} | Зрізаний октаедр | Зрізаний кубооктаедр | Ромбозрізаний ікосододекаедр | ||
Зауважимо двоїстість між кубом і октаедром і між додекаедром і ікосаедром. Також, частково внаслідок самодвоїстості тетраедра, тільки одне архімедове тіло має тільки одну тетраедричну симетрію.
- Аперіодична мозаїка
- Архімедів граф
- Однорідний многогранник
- Тороїдальний многогранник
- Квазікристал
- Напівправильний многогранник
- Правильний многогранник
- ↑ а б в Grünbaum, 2009.
- ↑ Field, 1997, с. 241—289.
- ↑ Malkevitch, 1988, с. 85.
- Field J. . Rediscovering the Archimedean Polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler // Archive for History of Exact Sciences. — Springer, 1997. — Vol. 50, no. 3-4. — ISSN 0003-9519.
- Grünbaum, Branko. . An enduring error // Elemente der Mathematik. — 2009. — Vol. 64, no. 3. — P. 89–101. — DOI:10.4171/EM/120.. Перепечатано в The Best Writing on Mathematics 2010. — Princeton University Press, 2011. — P. 18–31.
- Malkevitch, Joseph. . Shaping Space: A Polyhedral Approach / M. Senechal, G. Fleck. — Boston : Birkhäuser, 1988. — P. 80–92.
- Pugh, Anthony. . Polyhedra: A visual approach. — California : University of California Press Berkeley, 1976. — ISBN 0-520-03056-7. Chapter 2
- Udaya, Jayatilake. . Calculations on face and vertex regular polyhedral // Mathematical Gazette. — 2005. — Vol. 89, no. 514. — P. 76–81.
- Williams, Robert. . The Geometrical Foundation of Natural Structure: A Source Book of Design. — Dover Publications, Inc., 1979. — ISBN 0-486-23729-X. (Section 3-9)
- Weisstein, Eric W. Archimedean solid(англ.) на сайті Wolfram MathWorld.
- Archimedean Solids [Архівовано 20 лютого 2016 у Wayback Machine.] by Eric W. Weisstein, Wolfram Demonstrations Project .
- Paper models of Archimedean Solids and Catalan Solids [Архівовано 20 лютого 2016 у Wayback Machine.]
- Free paper models (nets) of Archimedean solids [Архівовано 6 лютого 2016 у Wayback Machine.]
- The Uniform Polyhedra [Архівовано 11 лютого 2008 у Wayback Machine.] by Dr. R. Mäder
- Virtual Reality Polyhedra [Архівовано 23 лютого 2008 у Wayback Machine.], The Encyclopedia of Polyhedra by George W. Hart
- Penultimate Modular Origami [Архівовано 15 липня 2010 у Wayback Machine.] by James S. Plank
- Interactive 3D polyhedra на Java
- Solid Body Viewer[недоступне посилання] Інтерактивний перегляд 3D-многогранників, який дозволяє зберегти модель у форматі svg, stl або obj.
- Stella: Polyhedron Navigator [Архівовано 9 липня 2010 у Wayback Machine.]: Програмне забезпечення для створення зображень, багато з яких є на цій сторінці.
- Paper Models of Archimedean (and other) Polyhedra [Архівовано 25 січня 2021 у Wayback Machine.]


 French
French Deutsch
Deutsch
