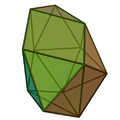
五角錐球狀屋頂 - 维基百科,自由的百科全书
 | |||
| 類別 | 詹森多面體 J89 - J90 - J91 | ||
|---|---|---|---|
| 識別 | |||
| 名稱 | 五角錐球狀屋頂 Disphenocingulum | ||
| 別名 | 五角錐球形屋根(日語) | ||
| 參考索引 | J90 | ||
| 鮑爾斯縮寫 | dawci | ||
| 性質 | |||
| 面 | 24 | ||
| 邊 | 38 | ||
| 頂點 | 16 | ||
| 歐拉特徵數 | F=24, E=38, V=16 (χ=2) | ||
| 組成與佈局 | |||
| 面的種類 | 4+2×8個三角形 4個正方形 | ||
| 頂點圖 | 4個(32.42) 4個(35) 8個(34.4) | ||
| 對稱性 | |||
| 對稱群 | D2d群 | ||
| 特性 | |||
| 凸 | |||
| 圖像 | |||
| |||
五角錐球狀屋頂(日語:五角錐球形屋根[1]、英語:Disphenocingulum)是一種由20個三角形和4個正方形組成的二十四面體[2],為詹森多面體的其中一個,索引為J90[3]。其可以藉由合併2個去除2個三角形面的球狀屋頂來構造,但它無法由柏拉圖立體(正多面體)和阿基米得立體(半正多面體)經過切割、增補而得來,是詹森多面體中的基本立體之一。詹森多面體是凸多面體,面皆由正多邊形組成但不屬於均勻多面體,共有92種。這些立體最早在1966年由諾曼·詹森(Norman Johnson)命名並給予描述[4]。
性質
[编辑]五角錐球狀屋頂共由24個面、38條邊和16個頂點組成[5][6][7][8]。其可以視為由2個去除2個三角形面的球狀屋頂三角形面重新排列合併而成,每個去除2個三角形面的球狀屋頂有12個面,三角形面重新排列合併完成後為二十四面體。其英文名稱字首「di-」表示兩個球狀屋頂,而字尾「-cingulum」(為belt(腰帶)的拉丁語)指的是12個分布於兩個正方形「屋頂」周圍的三角形的腰帶,兩者彼此旋轉90度互相接合[7]。雖然這24個面皆為正多邊形,但由於其有多種頂角,不滿足點可遞的特性,因此不屬於均勻多面體,這類立體早在1966年由諾曼·詹森(Norman Johnson)命名並給予描述[4]。
在組成五角錐球狀屋頂的24個面中,有20個三角形面和4個正方形面[6][8]。在其16個頂點中,有4個是5個三角形的公共頂點[8],在頂點圖中可以用[35]來表示[9]、還有8個頂點是4個三角形和1個正方形的公共頂點,在頂點圖中可以用[34,4]來表示[9]、剩下的4個頂點是2個三角形和2個正方形的公共頂點[8],在頂點圖中可以用[32,42]來表示[9]。
體積與表面積
[编辑]而其體積約為3.7776453418585752429[6]。
頂點座標
[编辑]令 ≈ 0.76713為下列多項式的實根
和和。
則邊長為2的五角錐球狀屋頂可以由下列頂點的軌道的並集在沿xz平面和yz平面鏡射所產生的空間對稱群之群作用下給出:[12]
相關多面體
[编辑]- 加長型球狀屋頂
(正方形附近的4個位置上各加上1個正三角形的球狀屋頂) - 五角錐球狀屋頂
(合併兩個移除了兩個正三角形的球狀屋頂)
參見
[编辑]參考文獻
[编辑]- ^ 整面凸多面体データ. mitani.cs.tsukuba.ac.jp. [2022-09-11]. (原始内容存档于2023-01-14).
- ^ Santiago Alvarez. Polyhedra in (Inorganic) Chemistry (PDF). Electronic Supplementary Information for Dalton Transactions. 2005 [2022-09-25]. (原始内容存档 (PDF)于2022-01-21).
- ^ Weisstein, Eric W. (编). Disphenocingulum. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 4.0 4.1 Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8
- ^ V.Bulatov. disphenocingulum. [2022-09-11]. (原始内容存档于2022-09-11).
- ^ 6.0 6.1 6.2 David I. McCooey. Johnson Solids: Disphenocingulum. [2022-09-07]. (原始内容存档于2022-09-11).
- ^ 7.0 7.1 The Disphenocingulum. qfbox.info. [2022-09-11]. (原始内容存档于2022-12-31).
- ^ 8.0 8.1 8.2 8.3 Disphenocingulum. polyhedra.tessera.li. [2022-09-11]. (原始内容存档于2023-01-03).
- ^ 9.0 9.1 9.2 Richard Klitzing. disphenocingulum, dawci. bendwavy.org. [2022-09-11]. (原始内容存档于2022-11-14).
- ^ Wolfram, Stephen. "Disphenocingulum". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Wolfram Research, Inc. Wolfram|Alpha Knowledgebase. Champaign, IL. 2020.
PolyhedronData[{"Johnson", 90}, "SurfaceArea"] - ^ Timofeenko, A. V. The non-platonic and non-Archimedean noncomposite polyhedra. Journal of Mathematical Sciences. 2009-10-17, 162 (5): 710–729. ISSN 1072-3374. S2CID 120114341. doi:10.1007/s10958-009-9655-0.


 French
French Deutsch
Deutsch