منطق ترکیبی - ویکی‌پدیا، دانشنامهٔ آزاد

مدارهای ترکیبی، نوعی از مدارهای منطقی هستند که خروجی آن‌ها در هر لحظه تابع مقادیر ورودی در همان لحظه است. این مدارها در برابر مدارهای ترتیبی مطرح می‌شوند.

هدف از تحلیل مدارهای ترکیبی، بدست آوردن تابع (های) خروجی برحسب متغیرهای ورودی، از روی دیاگرام، است. پس:
1- نخست، خروجی‌های همه گیت‌ها نامگذاری می‌شوند؛
2- تابع‌های خروجی هر گیت، از طبقه اول، برحسب ورودی‌های خودش نوشته می‌شوند؛
3- در آخر متغیرهای ورودی جایگزین نام‌ها می‌شوند.
بنا بر این، برای دیاگرام نمونه داریم:
T1=X’YZ
T2=XY’Z
F=T1+T2=X’YZ+XY’Z

1. تعریف مسئله؛
2. تعیین تعداد متغیرهای ورودی و تابع‌های خروجی؛
3. تخصیص حروف نمادین به ورودی‌ها و خروجی ها؛
4. تشکیل جدول درستی، که رابطهٔ بین ورودی‌ها و خروجی‌ها را آشکار می‌کند؛
5. بدست آوردن تابع بول ساده شده برای هر خروجی؛
6. رسم مدار منطقی.

• جمع کننده:

نیم جمع کننده: مدار ترکیبی که دو رقم دودویی را با هم جمع می کند نیم جمع کننده می نامند.

مشاهده می‌شود که عمل جمع دو عدد تک بیتی توسط 2 گیت AND و XOR قابل انجام است^[۱]

نحوه کار :

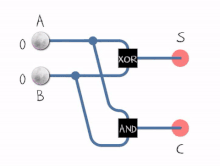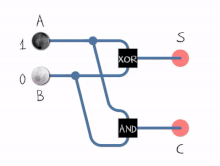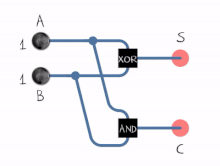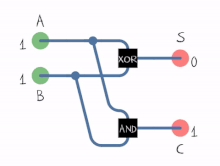
تمام جمع کننده: مداری که سه رقم دودویی را جمع کند (جمع دو رقم دودویی و یک رقم نقلی حاصل از ستون قبلی)، تمام جمع کننده نامیده می شود.

که در این مدار ها S حاصل جمع دو رقم، C رقم نقلی خروجی، x و y دو رقم جمع شونده و z رقم نقلی طبقه ی با ارزش کمتر.

• مانو، موریس. طراحی دیجیتال.
• لوینیک، وبسایت، برق و الکترونیک.