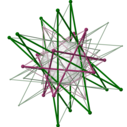
Poligon Petrie
În geometrie, un poligon Petrie a unui politop regulat cu n dimensiuni este un poligon strâmb în care fiecare (n − 1) laturi consecutive (dar nu n) aparțin uneia dintre fațete. Poligonul Petrie al unui poligon regulat este poligonul regulat în sine; cel al unui poliedru regulat este un poligon strâmb astfel încât fiecare două laturi consecutive (dar nu și trei) să aparțină uneia dintre fețe.[1] Poligoanele Petrie poartă numele matematicianului John Flinders Petrie.
Pentru fiecare politop regulat există o proiecție ortogonală pe un plan astfel încât un poligon Petrie să devină un poligon regulat, cu restul proiecției în interiorului său. Planul respectiv este planul Coxeter al grupului de simetrie al poligonului, iar numărul laturilor, h, este numărul Coxeter al grupului Coxeter. Aceste poligoane sunt utile la vizualizarea structurii simetrice a politopurilor regulate de ordin superior (din dimensiuni superioare).
În general, poligoanele Petrie pot fi definite pentru orice graf încorporat. Ele formează fețele unei alte încorporări în același grafic, de obicei pe o suprafață diferită, numită dual Petrie.[2]
Istoric
[modificare | modificare sursă]John Flinders Petrie (1907–1972) a fost singurul fiu al egiptologului Flinders Petrie. S-a născut în 1907 și ca elev a avut aptitudini remarcabile pentru matematică. Dacă se concentra intens, putea răspunde la întrebări despre obiecte 4-dimensionale complicate vizualizându-le.
El a remarcat primul importanța poligoanelor strâmbe regulate care apar pe suprafața poliedrelor regulate și a politopurilor de ordin super. Coxeter a explicat în 1937 cum el și Petrie au început să extindă subiectul clasic al poliedrelor regulate:
- „Într-o zi din 1926, J. F. Petrie mi-a spus cu mult entuziasm că a descoperit două noi poliede regulate; infinite dar fără vârfuri false. Când neîncrederea mea a început să scadă, mi le-a descris: unul format din pătrate, șase la fiecare vârf și unul format din hexagoane, patru la fiecare vârf.”[3]
În 1938 Petrie a colaborat cu Coxeter, Patrick du Val și H.T. Flather pentru a redacta în vederea publicării a lucrării The Fifty-Nine Icosahedra (română Cele cincizeci și nouă de icosaedre).[4] Înțelegând utilitatea geometrică a poligoanelor strâmbe folosite de Petrie, Coxeter le-a numit după prietenul său când a scris Politopuri regulate. Ideea poligoanelor Petrie a fost extinsă mai târziu la politopurile semiregulate.
Poligoanele Petrie ale poliedrelor regulate
[modificare | modificare sursă]Dualele regulate, {p,q} și {q,p}, sunt conținute în același poligon Petrie. În imaginile compușilor duali din dreapta se poate vedea că poligoanele lor Petrie au intersecții perpendiculare în punctele de tangență ale laturilor cu o sferă comună.
| Pătrat | Hexagon | Decagon | ||
|---|---|---|---|---|
 |  |  | 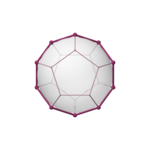 |  |
| tetraedru {3,3} | cub {4,3} | octaedru {3,4} | dodecaedru {5,3} | icosaedru {3,5} |
| centrat pe laturi | centrat pe vârfuri | centrat pe fețe | centrat pe fețe | centrat pe vârfuri |
| V:(4,0) | V:(6,2) | V:(6,0) | V:(10,10,0) | V:(10,2) |
| Poligoanele Petrie sunt conturul acestor proiecții ortogonale. | ||||
Poligoanele Petrie ale poliedrelor Kepler–Poinsot sunt hexagoane {6} și decagrame {10/3}.
| Hexagon | Decagramă | ||
|---|---|---|---|
 |  |  |  |
| Marele dodecaedru {5,5/2} | Micul dodecaedru stelat {5,5/2} | Marele icosaedru {3,5/2} | Marele dodecaedru stelat {5/2,3} |
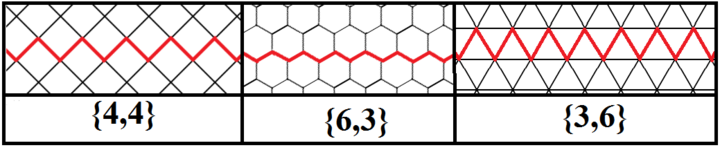
Poligoanele regulate infinite (apeirogoane) pot fi, de asemenea, definite ca fiind poligoanele Petrie ale placărilor regulate, având unghiuri de 90, 120 și 60 de grade ale fețelor lor pătrate, hexagonale și, respectiv, triunghiulare.
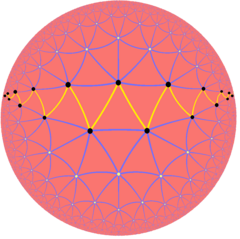
Poligoanele strâmbe regulate infinite există, de asemenea, ca poligoane Petrie ale placărilor hiperbolice regulate, cum ar fi placările triunghiulare de ordinul 7, {3,7}:
Poligoanele Petrie ale policorurilor regulate (4-politopuri)
[modificare | modificare sursă]Poligoanele Petrie ale policorurilor regulate {p, q ,r} pot fi și ele trasate.
 {3,3,3} 5-celule 5 laturi V:(5,0) | 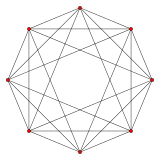 {3,3,4} 16-celule 8 laturi V:(8,0) |  {4,3,3} tesseract 8 laturi V:(8,8,0) |
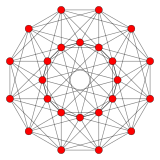 {3,4,3} 24-celule 12 laturi V:(12,6,6,0) |  {5,3,3} 120-celule 30 laturi V:((30,60)3,603,30,60,0) | 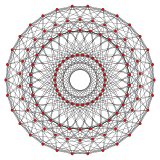 {3,3,5} 600-celule 30 laturi V:(30,30,30,30,0) |
Poligoanele Petrie ale politopurilor regulate și uniforme
[modificare | modificare sursă]Poligoanele Petrie sunt utile pentru vizualizarea politopurilor din patru dimensiuni și superioare.
Hipercuburi
[modificare | modificare sursă]Un hipercub din dimensiunea n are un poligon Petrie cu 2n laturi, care este și numărul fațetelor sale.
Deci, fiecare dintre (n−1)-cuburi care îi formează suprafața are n−1 fețe între laturile poligonului Petrie.
| Hipercuburi | ||
|---|---|---|
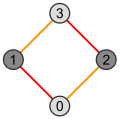
| Digonul Petrie al 1-cubului arată identic cu 1-cubul. Dar 1-cubul are o singură latură, în timp ce digonul are două. Imaginile arată cum poligonul Petrie pentru dimensiunea n+1 poate fi construit din cel pentru dimensiunea n:
Laturile fiecărui poligon Petrie aparțin următoarelor dimensiuni: | ||
| Pătrat | Cub | Tesseract |
 |  |  |
 | 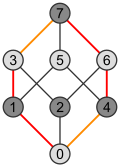 |  |
Note
[modificare | modificare sursă]- ^ en F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Kaleidoscopes: Selected Writings of H. S. M. Coxeter, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6 (Definition: paper 13, Discrete groups generated by reflections, 1933, p. 161)
- ^ en Gorini, Catherine A. (), Geometry at Work, MAA Notes, 53, Cambridge University Press, p. 181, ISBN 9780883851647
- ^ en H.S.M. Coxeter (1937) "Regular skew polyhedral in three and four dimensions and their topological analogues", Proceedings of the London Mathematical Society (2) 43: 33 to 62
- ^ H.S.M. Coxeter, Patrick du Val, H.T. Flather, J.F. Petrie (1938) The Fifty-nine Icosahedra, University of Toronto studies, mathematical series 6: 1–26
- ^ en Robert Steinberg, [https://www.cambridge.org/core/journals/canadian-journal-of-mathematics/article/on-the-number-of-sides-of-a-petrie-polygon/F66E7EF633FB67A3D0209A5DF9F51195 On the Number of Sides of a Petrie Polygon, Canadian Journal of Mathematics, vol. 10, 1958, pp. 220–221, DOI: https://doi.org/10.4153/CJM-1958-025-3, Published online by Cambridge University Press: 20 november 2018, accesat 2021-01-20
Bibliografie
[modificare | modificare sursă]- en Coxeter, H. S. M. (1947, 63, 73) Regular Polytopes, 3rd ed. New York: Dover, 1973. (sec 2.6 Petrie Polygons pp. 24–25, and Chapter 12, pp. 213–235, The generalized Petrie polygon )
- en Coxeter, H.S.M. (1974) Regular complex polytopes. Section 4.3 Flags and Orthoschemes, Section 11.3 Petrie polygons
- en Ball, W. W. R. and H. S. M. Coxeter (1987) Mathematical Recreations and Essays, 13th ed. New York: Dover. (p. 135)
- en Coxeter, H. S. M. (1999) The Beauty of Geometry: Twelve Essays, Dover Publications LCCN 99-35678
- en Peter McMullen, Egon Schulte (2002) Abstract Regular Polytopes, Cambridge University Press. ISBN: 0-521-81496-0
- en Steinberg, Robert,On the Number of Sides of a Petrie Polygon
Legături externe
[modificare | modificare sursă] Materiale media legate de poligon Petrie la Wikimedia Commons
Materiale media legate de poligon Petrie la Wikimedia Commons- en Eric W. Weisstein Petrie Polygon, (română Poigon Petrie) la Mathworld
- en Eric W. Weisstein Hypercube Graph, (română Graful hipercubului) la Mathworld
- en Eric W. Weisstein Cross polytope graph, (română Graful hiperoctaedrului) la Mathworld
- en Eric W. Weisstein 24-cell graph, (română Graful lui 24-celule) la Mathworld
- en Eric W. Weisstein 120-cell graph, (română Graful lui 120-celule) la Mathworld
- en Eric W. Weisstein 600-cell graph, (română Graful lui 600-celule) la Mathworld
- en Eric W. Weisstein Gosset Graph (321), (română Graful politopului Gosset 321) la Mathworld


 French
French Deutsch
Deutsch