Decagramă

Decagramă regulată
Tip	figură poligonală regulată
Laturi și vârfuri	10
Simbol Schläfli	{10/3} t{5/3}
Diagramă Coxeter
Grup de simetrie	Diedrală (D10)
Unghi interior (grade)	72
Poligon dual	autoduală
Proprietăți	stelată, circumscriptibilă, echilaterală, izogonală, izotoxală

În geometrie o decagramă este un poligon stelat cu zece vârfuri. Există o decagramă regulată, care are vârfurile unui decagon regulat, dar conectată din trei în trei vârfuri. Simbolurile sale Schläfli sunt {10/3} sau t{5/3}.^[1]

Denumirea de decagramă provine din prefixul numeric deca- și sufixul din greacă γραμμῆς (grammēs) cu sensul de dreaptă.^[2]

Pentru o decagramă regulată {10/3} cu lungimea laturilor 1, proporțiile punctelor de intersecție pe fiecare latură sunt cele din imaginea de alături.

Se poate verifica că suma acestor cinci distanțe este egală cu 1, deoarece

${\displaystyle 3({\sqrt {5}}-2)+2\left({\frac {1}{2}}(7-3{\sqrt {5}})\right)=1,}$

și că latura decagonului regulat (distanța dintre două vârfuri consecutive), coincide cu suma primelor două mărimi și este egală cu

${\displaystyle ({\sqrt {5}}-2)+{\frac {1}{2}}(7-3{\sqrt {5}})={\frac {1}{2}}(3-2{\sqrt {5}})=0,3819660113\ldots }$

Aria unei decagrame regulate este dublul ariei unei pentagrame regulate {5/2} cu aceeași lungime a laturii.^[3] Întucât aria unei pentagrame regulate cu latura de lungime a este:^[4]

${\displaystyle A=0,5{\sqrt {5(5-2{\sqrt {5}})}}\,l^{2},}$

unde ${\displaystyle l=a/\varphi }$, cu ${\displaystyle \varphi =1,618034\ldots }$ (secțiunea de aur),

aria decagramei este:

${\displaystyle A={\frac {1}{\varphi ^{2}}}{\sqrt {5(5-2{\sqrt {5}})}}\,a^{2},}$

Pentru a = 1, aria este ≈0,6205414.

Decagramele au fost folosite ca unul dintre motivele decorative în plăcile decorative girih.^[5]

Un poligon izotoxal are două vârfuri și o latură. Există forme de decagrame izotoxale, care alternează vârfuri la două raze. Fiecare formă are libertatea alegerii unui unghi. În figura de mai jos, cea din stânga este o variantă cu înfășurare dublă a unui pentagon {5}, cea din dreapta este o variantă cu înfășurări duble a unei pentagrame {5/2}, iar cea din mijloc este varianta decagramei regulate, {10/3}.

{(5/2)α}

{(5/3)α}

{(5/4)α}

O decagramă obișnuită este o poligramă cu 10 laturi, reprezentată prin simbolul {10/n}, care are aceleași vârfuri ca și decagonul regulat. Doar una dintre aceste poligrame, {10/3} (care leagă fiecare al treilea vârf), formează un poligon stelat regulat, dar există și trei poligrame cu zece vârfuri care pot fi interpretate drept compuși regulați:^[6][7]

• {10/5} este un compus din cinci digoane degenerate 5{2}
• {10/4} este un compus din două pentagrame 2{5/2}
• {10/2} este un compus din două pentagoane 2{5}.

Formă	Convex	Compus	Stelat	Compuși
Imagine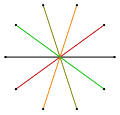
Simbol	{10/1} = {10}	{10/2} = 2{5}	{10/3}	{10/4} = 2{5/2}	{10/5} = 5{2}

{10/2} poate fi văzut ca echivalentul bidimensional al compusului de dodecaedru și icosaedru tridimensional și compusului de 120-celule și 600-celule cvadridimensional; adică compusul a două politopuri pentagonale în pozițiile lor duale respective.

{10/4} poate fi văzut ca echivalentul bidimensional al compusului de micul dodecaedru stelat și marele dodecaedru sau al compusul de marele icosaedru și marele dodecaedru stelat din motive similare. Are șase analogi în cvadridimensional, doi dintre aceștia fiind compuși de două politopuri stelate autoduale, ca pentagrama însăși; compusul de două mari 120-celule și compusul de două mari 120-celule stelat.

Trunchieri mai mari ale pentagonului regulat și pentagramei pot produce forme de poligoane stelate intermediare cu zece vârfuri egal distanțate și laturi de două lungimi care rămân tranzitive pe vârfuri (oricare două vârfuri pot fi transformate unul în celălalt printr-o simetrie a figurii).^[8][9][10]

Trunchieri izogonale ale pentagonului și pentagramei

Cvasiregulat	Izogonal		Cvasiregulat Dublă acoperire
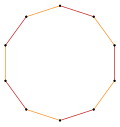t{5} = {10}		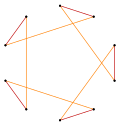	t{5/4} = {10/4} = 2{5/2}
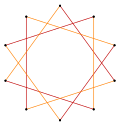t{5/3} = {10/3}			t{5/2} = {10/2} = 2{5}

Portal Matematică

• Materiale media legate de decagramă la Wikimedia Commons