Пентагональный икоситетраэдр — Википедия
| Пентагональный икоситетраэдр | |||
|---|---|---|---|
 «Правый» вариант (вращающаяся модель, 3D-модель) | |||
 «Левый» вариант (вращающаяся модель, 3D-модель) | |||
| Тип | каталаново тело | ||
| Свойства | выпуклый, изоэдральный, хиральный | ||
| Комбинаторика | |||
| Элементы |
| ||
| Грани | неправильные пятиугольники: | ||
| Конфигурация вершины | 8+24(53) 6(54) | ||
| Конфигурация грани | V3.3.3.3.4 | ||
| Двойственный многогранник | курносый куб | ||
| | |||
| Классификация | |||
| Обозначения | gC | ||
| Группа симметрии | O (хиральная октаэдрическая) | ||
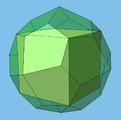
Пентагона́льный икоситетра́эдр (от др.-греч. πέντε — «пять», γωνία — «угол», εἴκοσι — «двадцать», τέτταρες — «четыре» и ἕδρα — «грань») — полуправильный многогранник (каталаново тело), двойственный курносому кубу. Составлен из 24 одинаковых неправильных пятиугольников.
Имеет 38 вершин. В 6 вершинах (расположенных так же, как вершины октаэдра) сходятся по 4 грани своими острыми углами; в 8 вершинах (расположенных так же, как вершины куба) сходятся по 3 грани теми тупыми углами, которые дальше от острого; в остальных 24 вершинах две грани сходятся своими тупыми углами, ближними к острому, и одна — тупым углом, дальним от острого.
У пентагонального икоситетраэдра 60 рёбер — 24 «длинных» и 36 «коротких».
В отличие от большинства других каталановых тел, пентагональный икоситетраэдр (наряду с пентагональным гексеконтаэдром) является хиральным и существует в двух разных зеркально-симметричных (энантиоморфных) вариантах — «правом» и «левом».
Метрические характеристики и углы
[править | править код]При определении метрических свойств пентагонального икоситетраэдра приходится решать кубические уравнения и пользоваться кубическими корнями — тогда как для ахиральных каталановых тел не требуется ничего сложнее квадратных уравнений и квадратных корней. Поэтому пентагональный икоситетраэдр, в отличие от большинства других каталановых тел, не допускает евклидова построения. То же верно и для пентагонального гексеконтаэдра, а также для двойственных им архимедовых тел.
Как и для курносого куба, при описании метрических свойств и углов пентагонального икоситетраэдра важную роль играет константа трибоначчи:

Если три «коротких» стороны грани имеют длину , то две «длинных» стороны имеют длину
Площадь поверхности и объём многогранника при этом выражаются как
Радиус вписанной сферы (касающейся всех граней многогранника в их инцентрах) при этом будет равен
радиус полувписанной сферы (касающейся всех рёбер) —
радиус окружности, вписанной в грань —
диагональ грани, параллельная одной из «коротких» сторон —
Описать около пентагонального икоситетраэдра сферу — так, чтобы она проходила через все вершины, — невозможно.
Все четыре тупых угла грани равны острый угол грани (между «длинными» сторонами) равен
Двугранный угол при любом ребре одинаков и равен
Ссылки
[править | править код]- Weisstein, Eric W. Пентагональный икоситетраэдр (англ.) на сайте Wolfram MathWorld.


 French
French Deutsch
Deutsch

![{\displaystyle t={\frac {1}{3}}\left(1+{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\sqrt[{3}]{19+3{\sqrt {33}}}}\right)\approx 1{,}8392868.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da6313c690fb2ddb56f3eb8743eb21e94dbe4496)










