رایانش کوانتومی - ویکی‌پدیا، دانشنامهٔ آزاد

این مقاله نیازمند ویکی‌سازی است. لطفاً با توجه به راهنمای ویرایش و شیوه‌نامه، محتوای آن را بهبود بخشید.

کامپیوتر کوانتومی (به انگلیسی: Quantum computer) ماشینی است که از پدیده‌ها و قوانین مکانیک کوانتوم مانند برهم نهی (Superposition) و درهم تنیدگی (Entanglement) برای رایانش استفاده می‌کند. رایانه‌های کوانتومی با رایانه‌های فعلی که با ترانزیستورها کار می‌کنند تفاوت اساسی دارند. ایده اصلی که در پس رایانه‌های کوانتومی نهفته‌است این است که می‌توان از خواص و قوانین فیزیک کوانتوم برای ذخیره‌سازی و انجام عملیات روی داده‌ها استفاده کرد. یک مدل تئوریک و انتزاعی از این ماشین‌ها، ماشین تورینگ کوانتومی (به انگلیسی: Quantum Turing Machine) است که رایانه کوانتومی جهانی (به انگلیسی: Universal Quantum Computer) نیز نامیده می‌شود.

اگر چه رایانش کوانتومی تازه در ابتدای راه قرار دارد، اما آزمایش‌هایی انجام شده که در طی آن‌ها عملیات محاسبات کوانتومی روی تعداد بسیار کمی از کیوبیت‌ها اجرا شده‌است. کشورهای چین و آمریکا در زمینه توسعه رایانه کوانتومی پیشگام هستند. تحقیقات نظری و عملی در این زمینه ادامه دارد و بسیاری از موسسات دولتی و نظامی از تحقیقات در زمینه رایانه‌های کوانتومی چه برای اهداف غیرنظامی و چه برای اهداف امنیتی (مثل تجزیه و تحلیل رمز، Cryptanalysis) حمایت می‌کنند. اگر رایانه‌های کوانتومی در مقیاس بزرگ ساخته شوند، می‌توانند مسائل خاصی را با سرعت خیلی زیاد حل کنند (برای مثال الگوریتم شُور، Shor's Algorithm). البته باید توجه داشت که توابعی که توسط رایانه‌های کلاسیک محاسبه پذیر (Computable) نیستند، توسط رایانه‌های کوانتومی نیز محاسبه پذیر نخواهند بود. این رایانه‌ها نظریه چرچ-تورینگ را رد نمی‌کنند. رایانه‌های کوانتومی فقط برای ما سرعت بیشتر را به ارمغان می‌آورند.

پیشرفت‌های محاسبات کوانتومی می‌تواند ارزشی معادل ۸۵۰ میلیارد دلار در ۱۵ تا ۳۰ سال آینده ایجاد کند که ۵ تا ۱۰ میلیارد دلار آن در پنج سال آینده تولید خواهد شد.^[۱]

تعریف سادهٔ نقطهٔ کوانتومی این است که یک ذره مادی کوچک، که افزایش یا کاهش یک الکترون خواص آن را به نحو ارزشمندی تغییر دهد. البته اتم‌ها نقطه کوانتومی محسوب می‌شوند، ولی توده‌های چند مولکولی نیز چنین‌اند. در زیست‌شیمی، نقاط کوانتومی گروه‌های اکسیداسیون-احیا خوانده می‌شوند. در نانوتکنولوژی به آن‌ها بیت‌های کوانتومی یا کیوبیت گفته می‌شود. اندازه آن‌ها در حد چند نانومتر است و از انواع مواد همچون سلنید کادمیوم -که رنگ‌های مختلفی را تولید می‌کند- ساخته می‌شوند. کاربردهای بالقوه آن‌ها در مخابرات و اپتیک است. نانوذرات فلورسنت -که تا پیش از تابش ماوراءبنفش نامرئی هستند- ساختار نانو بلوری قادر به تغییر رنگ از دیگر تعاریف آنهاست. نقاط کوانتومی از دیگر مواد فلورسنت انعطاف بیشتری دارد؛ لذا استفاده از آن‌ها در ساخت رایانه‌های نانومقیاس بهره‌گیرنده از نور برای پردازش اطلاعات مناسب است.

رؤیای محاسبات ماشینی یا ماشینی که بتواند مسائل را در اشکال گوناگون حل کند کمتر از دو قرن است که زندگی بشر را به‌طور جدی دربر گرفته‌است. اگر از ابزارهایی نظیر چرتکه و برخی تلاش‌های پراکنده دیگر در این زمینه بگذریم، شاید بهترین شروع را بتوان به تلاش‌های «چارلز بابیج» و «بلز پاسکال» با ماشین محاسبه مکانیکی شان نسبت داد. با گذشت زمان و تا ابتدای قرن بیستم تلاش‌های زیادی جهت بهبود ماشین محاسب مکانیکی صورت گرفت که همه آن‌ها بر پایه ریاضیات دهدهی (decimal) بود، یعنی این ماشین‌ها محاسبات را همان‌طور که ما روی کاغذ انجام می‌دهیم انجام می‌دادند.

تحول بزرگ در محاسبات ماشینی در ابتدای قرن بیستم شروع شد. این زمانی است که الگوریتم و مفهوم فرایندهای الگوریتمی (algorithmic processes) به سرعت در ریاضیات و به تدریج سایر علوم رشد کرد. ریاضیدانان شروع به معرفی سیستم‌های جدیدی برای پیاده‌سازی الگوریتمی کلی کردند که در نتیجه آن، سیستم‌های انتزاعی محاسباتی به وجود آمدند. در این میان سهم برخی بیشتر از سایرین بود. آنچه امروزه آن را دانش رایانه یا الکترونیک دیجیتال می‌نامیم مرهون و مدیون کار ریاضیدان برجسته انگلیسی به نام «آلن تورینگ» (Alan Turing) است. وی مدلی ریاضی را ابداع کرد که آن را ماشین تورینگ می‌نامیم و اساس تکنولوژی دیجیتال در تمام سطوح آن است. وی با پیشنهاد استفاده از سیستم دودویی برای محاسبات به جای سیستم عدد نویسی دهدهی که تا آن زمان در ماشین‌های مکانیکی مرسوم بود، انقلابی عظیم را در این زمینه به وجود آورد.

پس از نظریه طلایی تورینگ، دیری نپایید که «جان فون نویمان» یکی دیگر از نظریه پردازان بزرگ قرن بیستم موفق شد ماشین محاسبه‌گری را بر پایه طرح تورینگ و با استفاده از قطعات و مدارات الکترونیکی ابتدایی بسازد. به این ترتیب دانش رایانه به تدریج از ریاضیات جدا شد و امروزه خود زمینه‌ای مستقل و در تعامل با سایر علوم به‌شمار می‌رود. گیتهای پیشرفته، مدارات ابر مجتمع، منابع ذخیره و بازیابی بسیار حجیم و کوچک، افزایش تعداد عمل در واحد زمان و غیره از مهم‌ترین این پیشرفت‌ها در بخش سخت‌افزاری محسوب می‌شوند.

در ۱۹۶۵ «گوردون مور» اظهار کرد که توان رایانه‌ها هر دو سال دو برابر خواهد شد. در تمام این سال‌ها، تلاش عمده در جهت افزایش قدرت و سرعت عملیاتی در کنار کوچک‌سازی زیر ساختها و اجزای بنیادی بوده‌است. نظریه مور در دهه‌های ۶۰ و ۷۰ میلادی تقریباً درست بود. اما از ابتدای دهه ۸۰ میلادی و با سرعت گرفتن این پیشرفت‌ها، شبهات و پرسش‌هایی در محافل علمی مطرح شد که این کوچک سازی‌ها تا کجا می‌توانند ادامه پیدا کنند؟ کوچک کردن ترانزیستورها و مجتمع کردن آن‌ها در فضای کمتر نمی‌تواند تا ابد ادامه داشته باشد زیرا در حدود ابعاد نانومتری اثرات کوانتومی از قبیل تونل زنی الکترونی بروز می‌کنند.

گرچه همیشه تکنولوژی چندین گام بزرگ از نظریه عقب است، بسیاری از دانشمندان در زمینه‌های مختلف به فکر رفع این مشکل تا زمان رشد فناوری به حد مورد نظر افتادند. به این ترتیب بود که برای نخستین بار در سال ۱۹۸۲ «ریچارد فاینمن» معلم بزرگ فیزیک و برنده جایزه نوبل، پیشنهاد کرد که باید محاسبات را از دنیای دیجیتال وارد دنیای جدیدی به نام کوانتوم کرد که بسیار متفاوت از قبلی است و نه تنها مشکلات گذشته و محدودیت‌های موجود را بر طرف می‌سازد، بلکه افق‌های جدیدی را نیز به این مجموعه اضافه می‌کند. این پیشنهاد تا اوایل دهه ۹۰ میلادی مورد توجه جدی قرار نگرفت تا بالاخره در ۱۹۹۴ «پیتر شور» از آزمایشگاه AT&T در آمریکا نخستین گام را برای محقق کردن این آرزو برداشت. به این ترتیب ارتباط نوینی بین نظریه اطلاعات و مکانیک کوانتومی شروع به شکل‌گیری کرد که امروز آن را محاسبات کوانتومی یا محاسبات نانومتری (nano computing) می‌نامیم. در واقع هدف محاسبات کوانتومی یافتن روش‌هایی برای طراحی مجدد ادوات شناخته شده محاسبات (مانند گیت‌ها و ترانزیستورها) به گونه ایست که بتوانند تحت اثرات کوانتومی، که در محدوده ابعاد نانومتری و کوچکتر بروز می‌کنند، کار کنند.

رایانه تنها بخشی از دنیایی است که ما آن را دنیای دیجیتالی می‌نامیم. پردازش ماشینی اطلاعات، در هر شکلی، بر مبنای دیجیتال و محاسبات کلاسیک انجام می‌شود. اما کمتر از یک دهه است که روش بهتر و قدرتمندتر دیگری برای پردازش اطلاعات پیش رویمان قرار گرفته که بر اساس مکانیک کوانتومی می‌باشد. این روش جدید با ویژگی‌هایی همراه است که آن را از محاسبات کلاسیک بسیار متمایز می‌سازد. گرچه محاسبات دانشی است که اساس تولد آن در ریاضیات بود، اما رایانه‌ها سیستم‌هایی فیزیکی هستند و فیزیک در آینده این دانش نقش تعیین‌کننده‌ای خواهد داشت. البته وجود تفاوت بین این دو به معنای حذف یکی و جایگزینی دیگری نیست. به قول «نیلز بور» گاهی ممکن است خلاف یک حقیقت انکار ناپذیر منجر به حقیقت انکار ناپذیر دیگری شود؛ بنابراین محاسبات کوانتومی را به عنوان یک زمینه و روش جدید و بسیار کارآمد مطرح می‌کنیم.

وجود چند پدیده مهم که مختص فیزیک کوانتومی است، آن را از دنیای کلاسیک جدا می‌سازد. این پدیده‌ها عبارتند از: برهم‌نهی(superposition)، تداخل (interference), درهم تنیدگی (Entanglement)، نا موج بیت (non determinism)، ناجایگزیدگی (non locality) و تکثیر ناپذیری (non clonability). برای بررسی اثرات این پدیده‌ها در این روش جدید، لازم است که ابتدا واحد اطلاعات کوانتومی را معرفی کنیم.

هر سیستم محاسباتی دارای یک پایه اطلاعاتی است که نماینده کوچک‌ترین میزان اطلاعات قابل نمایش، چه پردازش شده و چه خام است. در محاسبات کلاسیک این واحد ساختاری را بیت می‌نامیم که گزیده واژه «عدد دودویی» است زیرا می‌تواند تنها یکی از دو رقم مجاز صفر و یک را در خود نگه دارد. به عبارت دیگر هر یک از ارقام یاد شده در محاسبات کلاسیک، کوچک‌ترین میزان اطلاعات قابل نمایش محسوب می‌شوند. پس سیستم‌هایی هم که برای این مدل وجود دارند باید بتوانند به نوعی این مفهوم را عرضه کنند. در محاسبات کوانتومی هم چنین پایه‌ای معرفی می‌شود که آن را کیوبیت (qubit) یا بیت کوانتومی می‌نامیم. اما این تعریف کیوبیت نیست و باید آن را همراه با مفهوم و نمونه‌های واقعی و فیزیکی درک کرد. در ضمن فراموش نمی‌کنیم که کیوبیت‌ها سیستم‌هایی فیزیکی هستند، نه مفاهیمی انتزاعی و اگر از ریاضیات هم برای توصیف آن‌ها کمک می‌گیریم تنها به دلیل ماهیت کوانتومی آن‌ها است.

در فیزیک کلاسیک برای نگهداری یک بیت از حالت یک سیستم فیزیکی استفاده می‌شود. در سیستم‌های کلاسیکی اولیه (رایانه‌های مکانیکی) از موقعیت مکانی دندانه‌های چند چرخ دنده برای نمایش اطلاعات استفاده می‌شد. از زمانی‌که حساب دودویی برای محاسبات پیشنهاد شد، سیستم‌های دو حالتی انتخاب‌های ممکن برای محاسبات عملی شدند. به این معنی که تنها کافی بود تا سیستمی دو حالت یا دو پیکربندی مشخص، متمایز و بدون تغییر داشته باشد تا بتوان از آن برای این منظور استفاده کرد. به همین جهت، از بین تمام کاندیداها، سیستم‌های الکتریکی و الکترونیکی برای این کار انتخاب شدند. به این شکل، هر بیت، یک مدار الکتریکی است که یا در آن جریان وجود دارد یا ندارد.

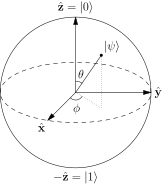
هر بیت کوانتومی یا کیوبیت عبارت است از یک سیستم دودویی که می‌تواند دو حالت مجزا داشته باشد. به عبارت فنی‌تر، کیوبیت یک سیستم دو بعدی کوانتومی با دوپایه به شکل و است. البته نمایش پایه‌ها یکتا نیست، به این دلیل که برخلاف محاسبات کلاسیک در محاسبات کوانتومی از چند سیستم کوانتومی به جای یک سیستم ارجح استفاده می‌کنیم. اولین کاندید برای نمایش کیوبیت استفاده از مفهوم اسپین است که معمولاً اتم هیدروژن برای آن به کار می‌رود. در اندازه‌گیری اسپین یک الکترون، احتمال به‌دست آمدن دو نتیجه وجود دارد: یا اسپین رو به بالاست که با آن را با نشان می‌دهیم و معادل است یا رو به پایین است که با نشان می‌دهیم و معادل است با |۱>|. بالا یا پایین بودن جهت اسپین در یک اندازه‌گیری از آنجا ناشی می‌شود که اگر اسپین اندازه‌گیری شده در جهت محوری باشد که اندازه‌گیری را در جهت آن انجام داده‌ایم، آن را بالا و اگر در خلاف جهت این محور باشد آن را پائین می‌نامیم. علاوه بر اسپین از وضع قطبش یک پرتو فوتونی و نیز سطوح انرژی مجزای یک اتم دلخواه نیز می‌توان به عنوان سیستم کیوبیتی استفاده کرد.

شاید بتوان مهم‌ترین تفاوت بیت و کیوبیت را در این دانست که بیت کلاسیک فقط می‌تواند در یکی از دو حالت ممکن خود قرار داشته باشد درحالی‌که بیت کوانتومی می‌تواند به‌طور بالقوه در بیش از دو حالت وجود داشته باشد. تفاوت دیگر در اینجاست که هرگاه بخواهیم می‌توانیم مقدار یک بیت را تعیین کنیم اما اینکار را در مورد یک کیوبیت نمی‌توان انجام داد. به زبان کوانتومی، یک کیوبیت را با عبارت نشان می‌دهیم. حاصل اندازه‌گیری روی یک کیوبیت حالت |o> را با احتمال C۱۲ و حالت |۱>| را با احتمال C۲۲ به‌دست می‌دهد. البته اندازه‌گیری یک کیوبیت حتماً یکی از دو نتیجه ممکن را به‌دست می‌دهد. از سوی دیگر اندازه‌گیری روی سیستم‌های کوانتومی حالت اصلی آن‌ها را تغییر می‌دهد. کیوبیت در حالت کلی در یک حالت برهم‌نهاده از دوپایه ممکن قرار دارد. اما در اثر اندازه‌گیری حتماً به یکی از پایه‌ها برگشت می‌کند. به این ترتیب هر کیوبیت، پیش از اندازه‌گیری‌شدن می‌تواند اطلاعات زیادی را در خود داشته باشد.

بین رایانه‌های کلاسیک و رایانه‌های کوانتومی نسل آینده تفاوت اساسی وجود دارد. یک رایانه کلاسیک بر اساس قوانین فیزیک کلاسیک دستورهای از پیش تعیین شده‌ای را اجرا می‌کند، اما یک رایانه کوانتومی دستگاهی است که یک پدیدهٔ فیزیکی را بر اساس مکانیک کوانتومی به صورت منحصربه‌فردی درمی‌آورد تا به صورت اساسی یک حالت جدید از پردازش اطلاعات را تشخیص دهد. در یک رایانه معمولی اطلاعات به صورت یک سری بیت کدگذاری می‌شوند و این بیت‌ها از طریق گیتهای منطقی بولین که سری هستند برای نتیجهٔ نهایی دستکاری می‌شوند به‌طور مشابه یک رایانه کوانتومی، کوبیت‌ها یا بیت‌های کوانتومی را با اجرای یک از گیت‌های کوانتومی دستکاری می‌کند و هر واحد انتقال بر روی یک تک کوبیت یا یک جفت کوبیت عمل می‌کند. با به کار بردن این کمیت‌های متوالی یک رایانه کوانتومی می‌تواند یک واحد انتقال پیچیده از طریق مجموعه‌ای از کوبیت‌ها در بعضی حالات ابتدایی ایجاد کند. پیشبرد پروژه ایجاد رایانه‌های کوانتومی در یک رایانه کوانتومی به جای استفاده از ترانزیستورها و مدارهای رایانه‌ای معمولی از اتم‌ها و سایر ذرات ریز برای پردازش اطلاعات استفاده می‌شود. یک اتم می‌تواند به عنوان یک بیت حافظه در رایانه عمل کند و جابجایی اطلاعات از یک محل به محل دیگر نیز توسط نور امکان می‌پذیرد.

• کریس مونرو و همکارانش در دانشگاه میشیگان برای ذخیره اطلاعات با استفاده از حالت مغناطیسی اتم از یک اتم کادمیم به دام افتاده در میدان الکتریکی استفاده کردند. در این روش انرژی توسط یک لیزر به درون اتم پمپاژ شده و اتم وادار به گسیل فوتونی می‌شود که رونوشتی از اطلاعات اتم را دربردارد و توسط آشکارساز قابل تشخیص است.
• ذخیره اطلاعات در رایانه‌ها به صورت سری‌هایی از بیت‌های با حالت‌های روشن و خاموش صورت می‌گیرد. در اتم کادمیم در صورتی که میدان‌های مغناطیسی کوچک هسته و الکترون‌های بیرونی در یک جهت قرار بگیرند روشن و در خلاف جهت خاموش محسوب می‌شوند. کریس مونرو گفته‌است: اتم کادمیم در هر یک از این حالات که باشد می‌تواند هزاران سال در همان حالت بماند.

در سال ۲۰۱۱ شرکت رایانه‌ای دی-ویو سیستمز اولین رایانهٔ کوانتومی قابل عرضه در بازار را معرفی کرد. این رایانه D-Wave One نام دارد و از یک پردازنده ۱۲۸ کیوبیتی بهره می‌گیرد. در سال ۲۰۱۳ هم رایانهٔ کوانتومی دی-ویو تو از همین شرکت عرضه شد. تعدادی از محققان، در مورد این دو رایانه ابراز شک و تردید کردند.

یک رایانه کوانتومی که دارای تعدادی بیت کوانتومی است، اساساً با رایانه کلاسیک که دارای همان تعداد بیت است متفاوت است. برای مثال برای نشان دادن حالت سیستم n بیت کوانتومی روی رایانه کلاسیک، احتیاج به ذخیره n ضریب مختلط است. اگرچه به نظر می‌رسد که بیت کوانتومی می‌تواند اطلاعات را به‌طور نمایی بیشتر از همتایان کلاسیک خود نگه دارد؛ نباید از این حقیقت بیتهای کوانتومی که فقط احتمال انطباق در همه حالت‌هایشان هستند، چشم پوشی کنیم. به این معنی که وقتی حالت نهایی بیت کوانتومی اندازه‌گیری شود، آن‌ها فقط در یکی از تنظیمات ممکن که قبلاً اندازه‌گیری شده‌اند یافت می‌شوند. علاوه بر این اگر فکر کنیم که بیتهای کوانتومی فقط در یک حالت ممکن قبل از اندازه‌گیری وجود داشته‌اند، نادرست است. چرا که این حقیقت وجود دارد که آن‌ها در حالت‌های منطبق قبل از اینکه اندازه‌گیری شوند روی نتایج احتمالی محاسبات تأثیر مستقیم دارند.

برای مثال رایانه کلاسیک اولیه را در نظر بگیرید که با حافظه ۳ بیت کار می‌کند. رایانه در هر زمان، یک توزیع احتمال با ۸ حالت مختلف دارد. اگر یک رایانه مطمئن باشد، پس قطعاً حالتی وجود دارد که احتمال وجود آن حالت ۱ است. اگر رایانه یک رایانه احتمالی (غیر قطعی) باشد، احتمال این وجود دارد که رایانه در هر یک از حالت‌های مختلف قرار بگیرد. ما می‌توانیم هریک از این حالت‌های احتمالی را با ۸ عدد توصیف کنیم. باید در نظر گرفت که مجموع احتمالات این حالتها برابر با یک خواهد بود.

حالت رایانه کوانتومی ۳ بیت با یک بردار ۸ بعدی توصیف می‌شود که Ket نامیده می‌شود؛ بنابراین به جای جمع کردن احتمال این حالتها، مجموع مربعات این حالتها را در نظر می‌گیریم که مقدار آن برابر با یک خواهد بود. علاوه بر این ضرائب اعداد مختلط هستند. گرچه دامنه این حالت‌ها با اعداد مختلط نشان داده می‌شود، فاز بین دو حالت یک پارامتر معنی دار است که این یک کلید تفاوت بین محاسبه کوانتوم و احتمال محاسبه کلاسیکی است.

اگر هر بیت بتواند در دو حالت صفر یا یک وجود داشته باشد، کیوبیت‌ها می‌توانند در هر لحظه صفر، یک، هر دوی آن‌ها یا هر عددی بین آن‌ها را اختیار کنند. به علاوه چنین قابلیتی، رایانه‌های کوانتومی می‌توانند همه این داده‌های گوناگون را هم در یک زمان پردازش کنند چون محدودیت تنها دو حالت صفر و یک وجود ندارد. در واقع در رایانش کوانتومی به جای پردازش به صورت سری، پردازش موازی انجام شده و زمانی که کاربر به اندازه‌گیری مقدار می‌پردازد تنها یکی از حالت‌های ممکن که احتمال بیشتری از سایرین دارد به نمایش در می‌آید. چنین کاری باعث افزایش سرعت پردازش مسائل در رایانه‌های کوانتومی به اندازه چندین میلیون برابر رایانه‌های کلاسیک باشد. کیوبیت‌ها می‌توانند در اتم‌ها، یون‌ها یا حتی موجودات کوچک‌تری مانند الکترون‌ها و فوتون‌ها ذخیره شوند^[۲]

حالت ۳ بیت کلاسیک و ۳ بیت کوانتوم، بردارهای ۸ بعدی هستند. آن‌ها به‌طور متفاوتی برای محاسبات کلاسیکی و کوانتومی عمل می‌کنند. برای محاسبه در هر زمینه، سیستم باید مقدار دهی شود.

محاسبه فاکتورگیری عدد صحیح به وسیلهٔ یک رایانه معمولی برای اعداد صحیح بزرگ، در صورتی که این اعداد حاصل چند عدد اول هستند (بعنوان مثال حاصل ضرب ۲ عدد اول ۳۰۰ رقمی) غیرممکن است. در مقایسه، یک رایانه کوانتومی می‌تواند به صورت مؤثری مشکل پیدا کردن این عامل‌ها را با استفاده از الگوریتم Shore حل کند. این قابلیت رایانه کوانتومی را قادر می‌سازد بسیاری از سیستم‌های رمزنگاری امروزه را رمز گشایی کند، به این معنی که یک الگوریتم زمانی (در تعداد ارقام عدد صحیح) چند جمله‌ای برای حل مسئله وجود خواهد داشت. به ویژه مبنای بسیاری از رمزهای کلید عمومی متداول، مشکل بودن فاکتورگیری اعداد صحیح (یا مسائل الگوریتم مجزای مربوط که به سادگی با الگوریتم Shore قابل حل است) شامل حالتهای مختلف RSA می‌باشد. این روش‌ها برای ایمن کردن صفحات WEB، رمز کردن ایمیل و بسیاری انواع دیگر دیتا بکار می‌رود. شکستن این‌ها پیامدهای مهمی برای محرمانگی و امنیت الکترونیکی خواهد داشت. با این حال بنظر نمی‌رسد سایر الگوریتم‌های رمزنگاری موجود با این الگوریتم‌ها شکسته شوند. برخی از الگوریتم‌های کلید عمومی بر مبنای مسائلی بجز فاکتورگیری اعداد صحیح و الگوریتم مجزا که الگوریتم Shore برای حل آن‌ها بکار می‌رود، مانند سیستم رمز McEliece مبتنی بر مسئله‌ای در تئوری کدینگ قابل حل باشند. سیستم‌های رمز Lattice نیز با رایانه‌های کوانتومی شکسته می‌شوند و یک الگوریتم زمانی چند جمله‌ای برای حل مسائل زیرگروه پنهان دو سطحی، که قابلیت شکستن بسیاری از رمزهای lattice را دارند، پیدا می‌کنند. ثابت شده که به‌کارگیری الگوریتم Grover برای شکستن الگوریتم متقارن (کلید مخفی) به روش حمله همه‌جانبه تقریباً نیاز به ${\displaystyle 2^{\frac {n}{2}}}$ الگوریتم رمز زیرین دارد که در مقایسه با ${\displaystyle 2^{n}}$ در حالت سنتی، به این معناست که طول کلید متقارن به صورت مؤثری نصف شده‌است. ۲۵۶–AES در برابر حمله‌ای که از الگوریتم Grover استفاده می‌کند همان میزان امنیت ۱۲۸-AES در برابر حملات همه‌جانبه سنتی دارد (ابعاد کلید را ببینید). رمزنگاری کوانتومی، برخی عملیات رمزنگاری کلید عمومی را به صورت بالقوه بهبود می‌بخشد. علاوه بر فاکتورگیری و الگوریتم‌های مجزا، الگوریتم‌های کوانتومی یک چند جمله‌ای سرعت بخش برای معروف‌ترین الگوریتم سنتی که برای بسیاری مسائل پیداشده، شامل شبیه‌سازی فرایندهای فیزیک کوانتومی در شیمی و فیزیک حالت جامد، تخمین چندجمله‌ای Jones و حل معادله Pell ارائه می‌کند. هیچ استدلال ریاضی که نشان دهد الگوریتم سنتی سریع معادلی را نتوان یافت، پیدا نشده و بعید هم به نظر می‌رسد. برای برخی مسائل، رایانه‌های کوانتومی یک چند جمله‌ای سرعت بخش ارائه می‌کنند. معروف‌ترین نمونه آن، جستجوی پایگاه داده کوانتومی است که با استفاده از الگوریتم Grover با پرسش‌های کمتر از پایگاه داده نسبت به روش سنتی حل می‌شود. این مزیت قابل اثبات است. نمونه‌های متعددی از سرعت بخشی کوانتومی برای مسائل مربوط به کوئری‌ها مانند یافتن توابع دو- به- یک و برآورد NAND trees اثبات شده‌است.

مسئله‌ای را با ۴ خصوصیت در نظر بگیرید:

1. تنها راه برای حل مسئله حدس زدن مکرر و امتحان زدن آنهاست.
2. تعداد پاسخهای احتمالی برای امتحان کردن مساوی تعداد ورودی هاست.
3. همه پاسخ‌های احتمالی یک زمان را برای امتحان کردن نیاز دارند.
4. هیچ نشانه‌ای دربارهٔ اینکه کدام پاسخ بهتر است وجود ندارد؛ مقادیر به صورت اتفاقی تولید و به ترتیب خاصی امتحان می‌شوند.

مثالی از آن رمز عبوریاب است که تلاش می‌کند تا رمز عبور را برای یک فایل رمز شده حدس بزند (با در نظر گرفتن حداکثر طول ممکن برای رمز عبور). برای مسائلی با ۴ خصوصیت فوق، زمان حل این مسئله برای رایانه کوانتومی، متناسب با جذر تعداد ورودی‌ها است. این سرعت را بسیار زیاد خواهد کرد و برخی مسائل را از سال‌ها به ثانیه‌ها خواهد رساند. از این رایانه‌های کوانتومی برای حمله به رمزهای متقارن مانند DES سه‌گانه و AES از طریق حدس زدن کلید مخفی استفاده می‌شود. الگوریتم Grover همچنین برای سرعت بخشی درجه دوم در جستجوهای همه‌جانبه پاره‌ای از مسائل مانند NP-complete بکار می‌رود. از آنجا که علوم شیمی و نانوتکنولوژی متکی بر درک سیستم‌های کوانتومی می‌باشند و این سیستم‌ها به روش سنتی قابل شبیه‌سازی نیستند، بسیاری بر این اعتقادند که شبیه‌سازی کوانتومی یکی از مهم‌ترین کاربردهای محاسبات کوانتومی است. چالش‌های فنی بسیاری در ایجاد یک رایانه کوانتومی در ابعاد بزرگ وجود دارد؛ بنابراین انتظار می‌رود این رایانه‌ها مسائل را بسیار سریع‌تر حل کنند. David DiVincenzo از شرکت IBM، الزامات زیر را برای یک رایانه کوانتومی ذکر کرده‌است:

• به لحاظ فیزیکی تعداد بیتهای کوانتومی قابل افزایش باشند؛
• به بیتهای کوانتومی بتوان مقادیر دلخواه داد؛
• Quantum gateها سریعتر از زمان ناهمدوسی باشند؛
• Gate عمومی ایجاد کرد؛
• بیتهای کوانتومی را بتوان به راحتی خواند.

یکی از بزرگ‌ترین چالش‌ها، کنترل یا حذف ناهمدوسی کوانتومی است. به این معنی که جداسازی سیستم از محیط آن درحالی‌که با جهان خارج تعامل دارد باعث ناهمدوسی سیستم می‌شود. این پدیده علمی برگشت‌ناپذیر است؛ زیرا یکپارچه نیست و در صورت عدم جلوگیری از آن، باید قویا کنترل شود. زمان‌های ناهمدوسی برای یک سیستم مناسب، به‌خصوص زمان واهلش سراسری T۲ (برای تکنولوژی‌های NMR و MRI زمان وافازی هم نامیده می‌شود)، عموماً در حرارت پایین بین چند نانو ثانیه تا چند ثانیه است. این مباحث برای رویکردهای اپتیکی بسیار پیچیده‌تر است؛ زیرا مقیاس‌های زمانی به میزان بسیار زیادی کوتاهتر می‌باشند و راهکاری که اغلب برای رفع آن ذکر می‌شود شکل‌دهی پالس نوری است. میزان خطا، عموماً با زمان عمل تا زمان ناهمدوسی نسبت دارد؛ بنابراین همه کارکردها باید بسیار سریع تر از زمان ناهمدوسی انجام شوند. اگر میزان خطا کم بود می‌توان از اصلاح خطای کوانتومی که خطاهای ناشی از ناهمدوسی را برطرف می‌کند استفاده کرد؛ بدینوسیله زمان محاسبه کل بیشتر از زمان ناهمدوسی خواهد بود. به‌طور معمول نرخ خطای هر Gate، از مرتبه ۴− می‌باشد(۱۰ به توان ۴−). به این معنا که هر Gate باید وظایف خود را در یک ده هزارم زمان ناهمدوسی سیستم انجام دهد. فراهم کردن این شرایط مقیاس‌پذیری برای بسیاری از سیستم‌ها مقدور است. درحالی‌که استفاده از اصلاح خطا هزینه افزودن تعداد زیادی بیت کوانتومی را نیز همراه دارد. تعداد این بیتهای کوانتومی الزامی برای فاکتورگیری اعداد صحیح با استفاده از الگوریتم Shore همچنان چند جمله‌ای است و بین L و ۲L می‌باشد که در آن L تعداد بیت‌هایی است که باید فاکتورگیری شوند. الگوریتم‌های اصلاح خطا، این عدد را با یک فاکتور اضافی L بزرگتر خواهند کرد. برای یک عدد ۱۰۰۰ بیتی نیاز به حدود ده هزار بیت کوانتومی بدون اصلاح خطا داریم. با اصلاح خطا این عدد به ده میلیون بیت کوانتومی خواهد رسید. توجه داشته باشید که این زمان حدود ۲L یا ده میلیون مرحله و روی MHz۱ حدود ۱۰ ثانیه خواهد بود. حالت دیگر برای مسئله ناهمدوسی پایدار، ایجاد یک هم‌بندی رایانه کوانتومی با anyons است که quasi-particleها به صورت رشته‌ها و متکی بر تئوری braid برای ایجاد دروازه‌های منطقی ثابت بکار می‌روند.

شرکت گوگل روز چهارشنبه ۲۳ اکتبر سال ۲۰۱۹ به‌طور رسمی اعلام کرد به برتری کوانتومی دست یافته‌است. محققان این شرکت در مقاله‌ای در نشریه علمی نیچر گفته‌اند با دستیابی به فناوری جدید، انجام محاسبه‌ای که با پیشرفته‌ترین رایانه حال حاضر جهان موسوم به «سامیت» ۱۰ هزار سال طول می‌کشد ، در ۳ دقیقه و ۲۰ ثانیه امکان‌پذیر شده‌است.^[۳]

دانشمندان به‌جای ترانزیستورهای سیلیکونی روی ریزتراشه‌ها، باید دستگاه‌های بدون لیزری را بسازند که اتم‌های واحد را به دام می‌اندازند و ماده را ابررسانا می‌کنند به‌طوری‌که جریان را بدون مقاومت منتقل کند و به‌این‌ترتیب می‌توان به خواص قابل تغییر کوانتومی و معماری‌های بالقوهٔ دیگر رسید. برای رسیدن به این هدف، ریزپردازنده باید در دمای صفر مطلق قرار بگیرد. در این دما ذرات از حداقل گرما برخوردار هستند. کنترل و ثابت نگه‌داشتن چنین سیستمی بسیار دشوار است زیرا اندک انرژی محیط می‌تواند منجر به فروپاشی کیوبیت‌ها و تجزیهٔ آن‌ها به بیت‌های معمولی و بسیار پرهزینه شود. در چنین شرایطی فقط قبل از فروپاشی وضعیت کوانتومی می‌توان به اجرای یک مجموعه از عملیات کوانتومی یا گیت پرداخت. محصور کردن تعداد زیاد کیوبیت منجر به فروپاشی سیستم می‌شود. هر کیوبیت اضافه، پیچیدگی ماشین را دو برابر خواهد کرد؛ بنابراین لازم است پالس‌های الکترومغناطیسی که مسئولیت کنترل سیستم را دارند به شکل بی‌نقصی تنظیم شوند.^[۴]

اسکات آرانسون در مقاله ای در سال ۲۰۰۸ بیان می‌کند که کامپیوترهای کوانتومی جادویی برای حل تمام مسائل نیستند. الگوریتم‌های کوانتومی در حل برخی مسائل برتری‌هایی نسبت به الگوریتم‌های کامپیوترهای کلاسیک دارند (برای مثال الگوریتم شور و گروور را ببینید) اما خیلی از محدودیت‌های کامپیوترهای کلاسیک را نیز دارند و این محدودیت‌ها با دشواری‌های ساخت کامپیوترهای کوانتومی مثل ناهمدوسی کوانتومی متفاوت هستند؛ یعنی حتی اگر روزی کامپیوتر کوانتومی بدون هیچ ناهمدوسی ساخته شود چنین محدودیت‌هایی هم چنان پابرجا خواهد بود.^[۵]

• مکانیک کوانتومی
• کیوبیت
• برهم نهی
• درهم تنیدگی

• مشارکت‌کنندگان ویکی‌پدیا. «Quantum computer». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۷ اوت ۲۰۱۰.
• منجمی، مجید. ممقانی راد، شکوفه. اسدیان حاج آقایی، گلایل. دنیایی نانو و الماسواره‌ها. انتشارات اندیشه سرا
• عشوریان، محسن. مقاره عابد، زهره. معلم، پیمان. کامپیوترهای کوانتومی-اصول (جلد اول). انتشارات دانشگاه آزاد اسلامی واحد شهر مجلسی
• معلم، پیمان. عشوریان، محسن. احسان پور، مریم. مقاره عابد، زهره. . کامپیوترهای کوانتومی-کاربردها (جلد دوم). انتشارات دانشگاه آزاد اسلامی واحد شهر مجلسی