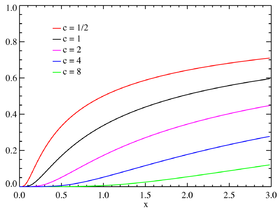
Distribution de Lévy Densité de probabilité pour différentes valeurs de c. Fonction de répartition pour différentes valeurs de c. Paramètres μ ∈ R {\displaystyle \mu \in \mathbb {R} } c > 0 {\displaystyle c>0\,} Support x ∈ ] μ , + ∞ [ {\displaystyle x\in ]\mu ,+\infty [\,} Densité de probabilité c 2 π ⋅ 1 ( x − μ ) 3 / 2 e − c 2 ( x − μ ) {\displaystyle {\sqrt {\frac {c}{2\pi }}}\cdot {\frac {1}{(x-\mu )^{3/2}}}\mathrm {e} ^{-{\frac {c}{2(x-\mu )}}}} Fonction de répartition e r f c c 2 ( x − μ ) {\displaystyle \mathrm {erfc} ~{\sqrt {\frac {c}{2(x-\mu )}}}\!} Espérance + ∞ {\displaystyle +\infty \,} Médiane c / 2 ( erf − 1 ( 1 / 2 ) ) 2 {\displaystyle c/2({\textrm {erf}}^{-1}(1/2))^{2}\,} μ = 0 {\displaystyle \mu =0} Mode c 3 {\displaystyle {\frac {c}{3}}\,} μ = 0 {\displaystyle \mu =0} Variance + ∞ {\displaystyle +\infty \,} Asymétrie non définie Kurtosis normalisé non défini Entropie 1 + 3 γ + ln ( 16 π c 2 ) 2 {\displaystyle {\frac {1+3\gamma +\ln(16\pi c^{2})}{2}}\,} Fonction génératrice des moments non définie Fonction caractéristique e i μ t − − 2 i c t {\displaystyle \mathrm {e} ^{\mathrm {i} \mu t-{\sqrt {-2\mathrm {i} ct}}}\,} modifier
En théorie des probabilités et en statistique , la loi de Lévy , nommée d'après le mathématicien Paul Lévy , est une loi de probabilité continue. En physique , plus précisément en spectroscopie , elle porte le nom de profil de van der Waals et décrit le profil de certaines raies spectrales .
Cette loi dépend de deux paramètres : un paramètre de position μ ∈ R {\displaystyle \mu \in \mathbb {R} } [ μ , ∞ [ {\displaystyle [\mu ,\infty [} paramètre d'échelle c {\displaystyle c}
Si X suit une loi de Lévy, on notera : X ∼ L e v y ( μ , c ) {\displaystyle X\sim \mathrm {Levy} (\mu ,c)}
Avec la loi de Cauchy et la loi normale , c'est l'une des trois à être stable par convolution et à posséder une densité de probabilité exprimable analytiquement.
La densité de probabilité de la loi de Lévy est donnée par :
f ( x ; μ , c ) = { c 2 π 1 ( x − μ ) 3 / 2 e − c 2 ( x − μ ) si x > μ 0 sinon {\displaystyle f(x;\mu ,c)={\begin{cases}\displaystyle {\sqrt {\frac {c}{2\pi }}}{\frac {1}{(x-\mu )^{3/2}}}\mathrm {e} ^{-{\frac {c}{2(x-\mu )}}}&{\text{ si }}x>\mu \\0&{\text{ sinon}}\end{cases}}} où μ ∈ R {\displaystyle \mu \in \mathbb {R} } paramètre de position et c > 0 {\displaystyle c>0} paramètre d'échelle . Comme toutes les lois stables , il existe une forme standard de la loi, définie par la densité f ( x ; 0 , 1 ) {\displaystyle f(x;0,1)} y = x − μ c {\displaystyle y={\frac {x-\mu }{c}}} f ( x ; μ , σ ) {\displaystyle f(x;\mu ,\sigma )}
La loi de Lévy possède une queue lourde , exprimée par la formule :
f ( x ; μ , c ) ∼ x → ∞ c 2 π 1 x 3 / 2 . {\displaystyle f(x;\mu ,c)\,{\underset {x\rightarrow \infty }{\sim }}\,{\sqrt {\frac {c}{2\pi }}}~{\frac {1}{x^{3/2}}}.} Cette propriété est illustrée par la représentation de la densité sur un repère log-log .
Densité de probabilité d la loi de Lévy sur un repère log-log.
La fonction de répartition de la loi de Lévy est donnée par :
F ( x ; μ , c ) = { erfc ( c / 2 ( x − μ ) ) si x > μ 0 sinon {\displaystyle F(x;\mu ,c)={\begin{cases}\displaystyle {\textrm {erfc}}\left({\sqrt {c/2(x-\mu )}}\right)&{\text{ si }}x>\mu \\0&{\text{ sinon}}\end{cases}}} où erfc est la fonction d'erreur complémentaire.
La fonction caractéristique de la loi de Lévy est :
φ ( t ; μ , c ) = e i μ t − − 2 i c t . {\displaystyle \varphi (t;\mu ,c)=\mathrm {e} ^{\mathrm {i} \mu t-{\sqrt {-2\mathrm {i} ct}}}.} On peut écrire cette fonction caractéristique sous la forme plus classique des lois stables :
φ ( t ; μ , c ) = e i μ t − | c t | 1 / 2 ( 1 − i sign ( t ) ) . {\displaystyle \varphi (t;\mu ,c)=\mathrm {e} ^{\mathrm {i} \mu t-|ct|^{1/2}~(1-\mathrm {i} ~{\textrm {sign}}(t))}.} La preuve de ce résultat utilise le théorème principal de Glasser .
Pour μ = 0 {\displaystyle \mu =0} n -ième moment de la loi de Lévy est donné formellement par :
m n = d e f c 2 π ∫ 0 ∞ e − c / 2 x x n x 3 / 2 d x . {\displaystyle m_{n}\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {\mathrm {e} ^{-c/2x}\,x^{n}}{x^{3/2}}}\,{\rm {d}}x.} Cette intégrale diverge pour tout n >0, ainsi les moments de la loi de Lévy ne sont pas définis. La fonction génératrice des moments est donnée formellement par :
M ( t ; c ) = d e f c 2 π ∫ 0 ∞ e − c / 2 x + t x x 3 / 2 d x . {\displaystyle M(t;c)\ {\stackrel {\mathrm {def} }{=}}\ {\sqrt {\frac {c}{2\pi }}}\int _{0}^{\infty }{\frac {\mathrm {e} ^{-c/2x+tx}}{x^{3/2}}}\,{\rm {d}}x.} L'intégrale diverge pour t > 0 {\displaystyle t>0}
Si X ∼ Levy ( μ , c ) {\displaystyle X\sim {\textrm {Levy}}(\mu ,c)\,} k X + b ∼ Levy ( k μ + b , k c ) {\displaystyle kX+b\sim {\textrm {Levy}}(k\mu +b,kc)\,} Si X ∼ Levy ( 0 , c ) {\displaystyle X\,\sim \,{\textrm {Levy}}(0,c)} X ∼ Inv-Gamma ( 1 2 , c 2 ) {\displaystyle X\,\sim \,{\textrm {Inv-Gamma}}({\tfrac {1}{2}},{\tfrac {c}{2}})} loi inverse-gamma ) La loi de Lévy est cas particulier de fonction de Pearson de type V. Si Y ∼ Normal ( μ , σ 2 ) {\displaystyle Y\,\sim \,{\textrm {Normal}}(\mu ,\sigma ^{2})} loi normale ) alors ( Y − μ ) − 2 ∼ Levy ( 0 , 1 / σ 2 ) {\displaystyle {(Y-\mu )}^{-2}\sim \,{\textrm {Levy}}(0,1/\sigma ^{2})} Si X ∼ Normal ( μ , 1 σ ) {\displaystyle X\sim {\textrm {Normal}}(\mu ,{\tfrac {1}{\sqrt {\sigma }}})\,} ( X − μ ) − 2 ∼ Levy ( 0 , σ ) {\displaystyle {(X-\mu )}^{-2}\sim {\textrm {Levy}}(0,\sigma )\,} Si X ∼ Levy ( μ , c ) {\displaystyle X\,\sim \,{\textrm {Levy}}(\mu ,c)} X ∼ Stable ( 1 / 2 , 1 , c , μ ) {\displaystyle X\,\sim \,{\textrm {Stable}}(1/2,1,c,\mu )\,} loi stable ) Si X ∼ Levy ( 0 , c ) {\displaystyle X\,\sim \,{\textrm {Levy}}(0,c)} X ∼ Scale-inv- χ 2 ( 1 , c ) {\displaystyle X\,\sim \,{\textrm {Scale-inv-}}\chi ^{2}(1,c)} loi inverse-χ² changée d'échelle) Si X ∼ Levy ( μ , c ) {\displaystyle X\,\sim \,{\textrm {Levy}}(\mu ,c)} ( X − μ ) − 1 2 ∼ FoldedNormal ( 0 , 1 / c ) {\displaystyle {(X-\mu )}^{-{\tfrac {1}{2}}}\sim \,{\textrm {FoldedNormal}}(0,1/{\sqrt {c}})} loi normale repliée ) 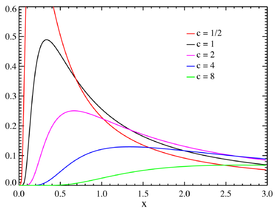



 French
French Deutsch
Deutsch

![{\displaystyle x\in ]\mu ,+\infty [\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba293074b6681b60f001fccf44dd8872d1deb506)


































