Четырёхугольный трапецоэдр — Википедия
| Четырёхугольный трапецоэдр | |
|---|---|
 | |
| Тип | трапецоэдр |
| Конвей | dA4 |
| Диаграмма Коксетера | |
| Грани | 8 дельтоидов |
| Рёбер | 16 |
| Вершин | 10 |
| Конфигурация граней | V4.3.3.3 |
| Группа симметрии | D4d, [2+,8], (2*4), order 16 |
| Группа вращений | D4, [2,4]+, (224), order 8 |
| Двойственный многогранник | Квадратная антипризма |
| Свойства | выпуклый, транзитивин по граням |
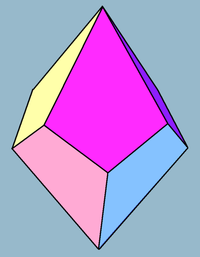
Четырёхугольный трапецоэдр или дельтоэдр — это второй многогранник в бесконечной серии многогранников с однородными гранями, которые являются двойственными антипризмам. Многогранник имеет восемь граней, которые конгруэнтны дельтоидам. Многогранник двойственен квадратной антипризме.
Использование для генерации сеток
[править | править код]Это тело используется как тестовый случай при генерации шестиугольных расчётных сеток[1][2][3][4][5], что упрощает тестирование по сравнению с тестом Роба Шнайдера в виде квадратной пирамиды с границами, поделёнными на 16 четырёхугольников. В этом контексте четырёхугольный трапецоэдр называют также кубическим октаэдром[3], четырёхугольным октаэдром[4], или восьмиугольным веретеном[5], поскольку тело имеет восемь четырёхугольных граней и однозначно определяется как комбинаторный многогранник этим свойством[3]. Добавление четырёх кубоидов (тел, топологически эквивалентных кубу) в сетку для кубического октаэдра даёт сетку для пирамиды Шнайдера[2]. Будучи простосвязным многогранником (то есть любой путь из рёбер разбивает грани на два несвязных множества) с чётным числом граней, кубический октаэдр может быть разложен на топологические кубоиды с кривыми гранями, которые прилегают друг к друг полными гранями и не нарушают границы четырёхугольников [1][5][6], что позволяет построить явно сетку для этого типа[4]. Однако неясно, можно ли получить такое разложение, в котором все кубоиды будут выпуклыми многогранниками с плоскими гранями[1][5].
Связанные многогранники
[править | править код]| Семейство трапецоэдров V.n.3.3.3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Многогранники |  |  |  |  |  |  |  |  | ||
| Мозаики |  |  |  |  |  |  |  |  |  | |
| Конфиг. | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | ...V10.3.3.3 | ...V12.3.3.3 | ...V∞.3.3.3 |
Четырёхугольный трапецоэдр является первым телом в серии двойственных плосконосых многогранников и мозаик с конфигурацией граней V3.3.4.3.n.
| 4n2 симметрии плосконосых мозаик: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия 4n2 | Сферическая | Евклидова | Компактная гиперболическая | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Плосконосые мозаики |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Гиро- мозаики |  |  |  |  | ||||
| Конфиг. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
Примечания
[править | править код]- ↑ 1 2 3 Eppstein, 1996, с. 58–67.
- ↑ 1 2 Mitchell, 1999, с. 228–235.
- ↑ 1 2 3 Schwartz, Ziegler, 2004, с. 385–413.
- ↑ 1 2 3 Carbonera, Shepherd, 2006, с. 435–452.
- ↑ 1 2 3 4 Erickson, 2013, с. 37–46.
- ↑ Mitchell, 1996, с. 465–476.
Литература
[править | править код]- David Eppstein. Linear complexity hexahedral mesh generation // Proceedings of the Twelfth Annual Symposium on Computational Geometry (SCG '96). — New York, NY, USA: ACM, 1996. — С. 58–67. — doi:10.1145/237218.237237.
- Mitchell S. A. The all-hex geode-template for conforming a diced tetrahedral mesh to any diced hexahedral mesh // Engineering with Computers. — 1999. — Т. 15, вып. 3. — С. 228–235. — doi:10.1007/s003660050018.
- Alexander Schwartz, Günter M. Ziegler. Construction techniques for cubical complexes, odd cubical 4-polytopes, and prescribed dual manifolds // Experimental Mathematics. — 2004. — Т. 13, вып. 4. — С. 385–413.
- Carlos D. Carbonera, Jason F. Shepherd,. A constructive approach to constrained hexahedral mesh generation // Proceedings of the 15th International Meshing Roundtable. — Berlin: Springer, 2006. — С. 435–452. — doi:10.1007/978-3-540-34958-7_25.
- Jeff Erickson. Efficiently hex-meshing things with topology // Proceedings of the Twenty-ninth Annual Symposium on Computational Geometry (SoCG '13). — New York, NY, USA: ACM, 2013. — С. 37–46. — doi:10.1145/2462356.2462403. Архивная копия от 10 августа 2017 на Wayback Machine
- Scott A. Mitchell. A characterization of the quadrilateral meshes of a surface which admit a compatible hexahedral mesh of the enclosed volume // STACS 96: 13th Annual Symposium on Theoretical Aspects of Computer Science Grenoble, France, February 22–24, 1996, Proceedings. — Berlin: Springer, 1996. — Т. 1046. — С. 465–476. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-60922-9_38.
Ссылки
[править | править код]- Paper model tetragonal (square) trapezohedron
- Weisstein, Eric W. Trapezohedron (англ.) на сайте Wolfram MathWorld.
Для улучшения этой статьи желательно:
|


 French
French Deutsch
Deutsch