Octaedru

Octaedru
(animație)
Descriere
Tip	poliedru platonic
Fețe	8
Laturi (muchii)	12
Vârfuri	6
χ	2
Configurația vârfului	3.3.3.3
Configurația feței	V4.4.4
Simbol Wythoff	4 | 2 3
Simbol Schläfli	{3,4} r{3,3} sau ${\displaystyle {\begin{Bmatrix}3\\3\end{Bmatrix}}}$
Simbol Conway	O aT
Diagramă Coxeter
Grup de simetrie	Oh, BC3, [4,3], (*432)
Grup de rotație	O, [4,3]+, (432)
Unghi diedru	109.47122° = arccos(−1⁄3)
Poliedru dual	Cub
Proprietăți	regulat, convex
Figura vârfului
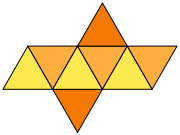
Desfășurată

În geometrie, un octaedru (plural, octaedre) este un poliedru cu opt fețe.

Un octaedru regulat este un poliedru platonic compus din opt triunghiuri echilaterale congruente (care se întâlnesc câte patru în vârfuri) și șase vârfuri. Octaedrul regulat mai poate fi descris ca fiind un corp în spațiu alcătuit din două piramide tetragonale regulate egale, unite la bazele lor.

Dacă se notează cu a lungimea muchiei octaedrului regulat, atunci raza sferei circumscrise (care trece prin toate cele șase vârfuri ale sale) este,

${\displaystyle r_{u}={\frac {a}{2}}{\sqrt {2}}\approx 0.707\cdot a}$

iar raza sferei înscrise (tangentă interioară la fiecare din fețele octaedrului) este dată de relația,

${\displaystyle r_{i}={\frac {a}{6}}{\sqrt {6}}\approx 0.408\cdot a}$

în timp ce raza medie, ce intersectează fiecare din cele opt muchii la mijlocul acestora, este

${\displaystyle r_{m}={\frac {a}{2}}=0.5\cdot a}$

Cele patru proiecții ortogonale "speciale" ale octaedrului sunt centrate pe muchie, pe vârf, pe față și, respectiv, perpendiculară.

Proiecții ortogonale

Centrat pe	Muchie	Față	Vârfuri	Față
Imagine
Simetrie proiectivă	[2]	[2]	[4]	[6]

Octaedrul poate fi reprezentat și ca o pavare sferică și proiectat pe un plan printr-o proiecție stereografică. Această proiecție este o conformă, păstrând unghiurile, dar nu ariile sau lungimile. Liniile drepte pe sferă sunt proiectate în plan ca arce de cerc.

Proiecție ortogonală	Proiecție stereografică

Octaedrul are ca echivalent în spațiul n-dimensional hiperoctaedrul.

Caută „Octaedru” în Wikționar, dicționarul liber.

• Compus de patru octaedre
• Compus de patru octaedre cu libertate de rotație
• Compus de cinci octaedre
• Compus de opt octaedre cu libertate de rotație
• Compus de zece octaedre
• Compus de douăzeci de octaedre
• Compus de douăzeci de octaedre cu libertate de rotație

• Materiale media legate de octaedru la Wikimedia Commons
• Paper model of the octahedron
• K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other S semi-Regular Polyhedra
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
  • Conway Notation for Polyhedra Try: dP4

Portal matematică

• en Klitzing, Richard. „3D uniform polyhedra”.  Cheie: oct

Familia antiprismelor n-gonale uniforme     v • d • m
Imagine poliedru												...	Antiprismă apeirogonală
Imagine pavare sferică												Imagine pavare plană
Configurația vârfului n.3.3.3	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

v • d • m Poliedru (categorie) 1–10 fețe Monoedru (1) · Diedru (2) · Triedru (3) · Tetraedru (4) · Pentaedru (5) · Hexaedru (6) · Heptaedru (7) · Octaedru (8) · Eneaedru (9) · Decaedru (10) 2–20 fețe Endecaedru (11) · Dodecaedru (12) · Tridecaedru (13) · Tetradecaedru (14) · Pentadecaedru (15) · Hexadecaedru (16) · Heptadecaedru (17) · Octadecaedru (18) · Eneadecaedru (19) · Icosaedru (20) >20 fețe Icositetraedru (24)  · Triacontaedru (30) · Icosidodecaedru (32) · Hexacontaedru (60) · Eneacontaedru (90) · Hectotriadioedru (132) · Apeiroedru (∞) (regulat) Noțiuni de bază față · latură · vârf · poliedru uniform (poliedru regulat · poliedru cvasiregulat · poliedru semiregulat) Poliedre convexe poliedru platonic · poliedru arhimedic · poliedru Catalan · poliedru Johnson Poliedre neconvexe poliedru Kepler–Poinsot · poliedru stelat (poliedru stelat uniform) · hemipoliedru Poliedre prismatice prismă · antiprismă · trunchi · cupolă · pană · piramidă · paralelipiped