Fibrato vettoriale

Questa voce sull'argomento geometria è solo un abbozzo.

Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento.

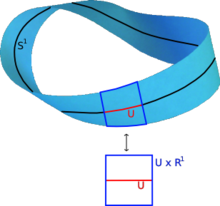
In matematica, un fibrato vettoriale è una costruzione che associa a ogni punto di una varietà topologica (o differenziabile) uno spazio vettoriale (generalmente reale o complesso). Si tratta quindi di un particolare fibrato, la cui fibra ha una struttura di spazio vettoriale.

Il fibrato tangente e il fibrato cotangente sono due esempi.

Un fibrato vettoriale reale è un fibrato che ha come fibra uno spazio vettoriale, cioè è una funzione continua suriettiva ${\displaystyle p\colon E\to B}$ fra spazi topologici tale che la controimmagine ${\displaystyle p^{-1}(x)}$ di ogni punto ${\displaystyle x\in B,}$ detta fibra sopra il punto ${\displaystyle x,}$ sia dotata di una struttura di spazio vettoriale reale. Si chiede inoltre che questa struttura vari in modo continuo al variare di ${\displaystyle x}$. Questa richiesta è formalizzata chiedendo che la proiezione sia localmente un prodotto. Più precisamente, per ogni punto ${\displaystyle x}$ dello spazio base ${\displaystyle B}$ esiste un intorno aperto ${\displaystyle U}$ del punto ${\displaystyle x}$ e un omeomorfismo:

${\displaystyle \phi \colon p^{-1}(U)\to U\times \mathbb {R} ^{k},}$

tale che:

${\displaystyle \mathrm {pr} _{1}\circ \phi =p}$

dove ${\displaystyle \mathrm {pr} _{1}\colon U\times \mathbb {R} ^{k}\to U}$ è la proiezione sul primo fattore. Si richiede inoltre che l'omeomorfismo preservi le strutture di spazi vettoriali, e cioè che l'omeomorfismo:

${\displaystyle \phi |_{p^{-1}(x')}:p^{-1}(x')\to \lbrace x'\rbrace \times \mathbb {R} ^{k},}$

sia anche un isomorfismo di spazi vettoriali, per ogni punto ${\displaystyle {x'}}$ dell'aperto ${\displaystyle U.}$

• M. Abate, F. Tovena, Geometria Differenziale, Springer, 2011, ISBN 978-88-470-1919-5.
• G. Gentili, F. Podestà, E. Vesentini, Lezioni di Geometria Differenziale, Torino, Bollati Boringhieri, 1995, ISBN 978-88-339-5556-8.
• Edoardo Sernesi, Geometria 2, Torino, Bollati Boringhieri, 1994, ISBN 978-88-339-5548-3.
• (EN) I. Kolář, P. Michor, J. Slovák, Natural operators in differential geometry (PDF), Springer-Verlag, 1993. URL consultato il 5 luglio 2013 (archiviato dall'url originale il 30 marzo 2017).

• Fibra (matematica)
• Fibrato
• Fibrato tangente
• Spazio vettoriale
• Varietà differenziabile
• Varietà topologica

• Wikimedia Commons contiene immagini o altri file su fibrato vettoriale

• Luca Tomassini, fibrato vettoriale, in Enciclopedia della scienza e della tecnica, Istituto dell'Enciclopedia Italiana, 2007-2008.
• (EN) vector bundle, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Fibrato vettoriale, su MathWorld, Wolfram Research.

V · D · M Topologia
Concetti di Topologia generale	Spazio topologico · Base · Prebase · Ricoprimento · Assiomi di chiusura di Kuratowski · Invariante topologico · Relazione di finezza · Partizione dell'unità · Proprietà dell'intersezione finita Sottoinsiemi Intervallo · Aperto · Intorno · Chiuso · Insieme localmente chiuso · Insieme chiuso-aperto · Parte interna · Chiusura · Frontiera · Insieme derivato · Insieme limite · Insieme perfetto · Insieme denso · Insieme mai denso Punti Punto isolato · Punto di accumulazione · Punto di aderenza Funzioni Funzione continua · Omeomorfismo · Funzione aperta · Funzione chiusa · Funzione propria · Contrazione · Retrazione · Germe di funzione · Funzione a supporto compatto Successioni Limite · Limite di una successione · Successione · Rete · Convergenza · Successione di Cauchy Teoremi Teorema di Weierstrass · Heine-Borel · Tichonov · Lemma del tubo · Urysohn · Tietze · Baire · Brouwer · punto fisso · Teorema di Borsuk · Teorema di Borsuk-Ulam · Teorema della curva di Jordan · Teorema della mappa di Riemann Applicazioni pratiche Topologia dello spazio-tempo · Teoria quantistica dei campi topologica · K-teoria ritorta · Topologia di rete · Controllo della topologia · Topologia molecolare
Spazi topologici	Topologie classiche Topologia banale · Spazio di Sierpiński · Cofinita · Topologia della semicontinuità inferiore · di Zariski · Euclidea · del limite inferiore o di Sorgenfrey · Discreta · Topologia degli interi equispaziati · Insieme reale esteso · Topologia di ordine · Piano di Moore · Topologia p-adica Costruzioni topologiche Topologia prodotto · Topologia di sottospazio · Topologia quoziente · Compattificazione (di Alexandrov · di Stone-Čech) · Cono · Bouquet · Rosa · Sospensione Topologie in Analisi funzionale Spazio funzionale · Topologia iniziale o debole · Topologia operatoriale · Topologia finale o forte · Topologia di Mackey · Topologia polare · Topologie operatoriali debole e forte Altri oggetti topologici Sfera · Palla · Toro · Corpo con manici · Bottiglia di Klein · Bottiglia di Klein solida · Anello · Nastro di Möbius · Retta proiettiva · Piano proiettivo · Superficie di Riemann · Nodo · Nodo torico · Link Frattali Insieme di Cantor · Spazio di Cantor · Polvere di Cantor · Spugna di Menger · Sfera di Alexander · Curva di Peano · Laghi di Wada Strutture miste Spazio vettoriale topologico · Gruppo topologico · Gruppo di Lie · Spazio uniforme · Algebra di Borel
Proprietà degli spazi topologici	Numerabilità Assioma di numerabilità · Spazio primo-numerabile · Spazio separabile · Spazio sequenziale Separazione Assioma di separazione · Spazio T0 · Spazio T1 · Spazio di Hausdorff · Spazio regolare · Spazio di Tichonov · Spazio normale Compattezza Spazio compatto · Spazio paracompatto · Spazio localmente compatto · Spazio di Lindelöf · Sottospazio relativamente compatto · Immersione compatta Connessione Spazio connesso · Spazio semplicemente connesso Metrizzabilità Spazio metrico · Spazio metrico completo · Spazio metrizzabile · Spazio ultrametrico · Spazio pseudometrico · Spazio polacco · Spazio normato · Spazio totalmente limitato Altre proprietà Spazio di Baire · Spazio topologico noetheriano · Spazio omogeneo · Orientazione
Topologia differenziale	Varietà (differenziabile · parallelizzabile · 3-varietà · 3-varietà irriducibile) · Atlante · Diffeomorfismo (locale · di Anosov) · Immersione · Curva · Superficie · Campo vettoriale · Fibrato (principale · vettoriale · Varietà fibrata) · Fibrato tangente · Spazio tangente · Fibrazione di Hopf · Varietà con bordo · Teorema dell'intorno tubolare · Somma connessa · Teorema di Kneser-Milnor · Congettura di geometrizzazione di Thurston · Cobordismo · Dimensione topologica · Topologia in dimensione bassa · Chirurgia di Dehn · Trasversalità · Eversione della sfera · Teoria delle foliazioni · Decomposizione JSJ
Topologia algebrica	Fondamenti Spazio semplicemente connesso · Gruppo fondamentale Omotopia Arco · Nerbo · Omotopia · Gruppi di omotopia Omologia e coomologia Omologia · Omologia singolare · Omologia ciclica · Algebra omologica · Coomologia di De Rham · Categoria abeliana Sollevamento Sollevamento · Teorema del sollevamento dell'omotopia · Teorema di unicità del sollevamento · Teorema di Van Kampen Topologia algebrica avanzata Grado topologico · Indice di avvolgimento · Indice di un campo vettoriale · Rivestimento · Numero di Betti · Successione di Mayer-Vietoris · Successione esatta · Successione spettrale · Complesso simpliciale · Complesso di celle · Complesso di catene · Schema simpliciale Superfici Caratteristica di Eulero · Formula di Eulero per i poliedri · Genere · Taglio · Superficie incompressibile · Classificazione delle superfici · Mapping class group · Teorema della palla pelosa · Teorema di Poincaré-Hopf · Congettura di Poincaré · Congettura di Hodge
Topologi di rilievo	Henri Poincaré · Felix Hausdorff · Georg Cantor · Eduard Čech · John Milnor · Pierre Samuel · Norman Steenrod · René Thom · Samuel Eilenberg · Andrej Nikolaevič Kolmogorov · Stephen Smale · Michael Atiyah · William Thurston · Marston Morse · Luitzen Brouwer

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica